露天煤矿含水边坡稳定性弹塑性有限元计算方法

付天光

(中煤科工能源投资有限公司，北京 100013)

在露天矿山开采中，采场周围通常形成几百米高的边坡，堆积矿物上覆岩土的排土场也形成几百米高的边坡。边坡稳定性是露天矿山开采的安全问题，也是重要的经济问题。

边坡岩土体的强度参数是边坡设计的重要依据，然而岩土体的强度对岩土体的含水率非常敏感。很多滑坡都是由于水的参与才发生的。

水对岩土材料强度的影响早已引起人们的重视，并开展了大量的研究工作。例如不同配合比下，三合土的粘聚力随含水率的变化存在最大值[1]。冻土的抗压强度随含水率的变化也存在最大值[2]。粉质黏土在最大干密度和最优含水率时抗剪强度最大，在最优含水率以前随含水率越大抗剪强度越大，在最优含水率以后随含水率越大抗剪强度越小；而高液限细粒土砾的含水量越大抗剪强度越小[3]。强度、黏聚力和内摩擦角随含水率呈非线性变化，在最优含水率附近存在一峰值；剪切过程中存在显著的剪胀性，随围压和含水率增大，剪胀性减弱；初始孔隙压力随含水率的增大而提高，随剪切的进行，先增大再减小；孔隙气压力与土样的体应变密切相关，剪缩时升高，剪胀时降低；在相同含水率情况下，孔隙气压力和孔隙水压力皆随围压增大而增大[4]。

水对边坡稳定性的影响表现在多方面：含水率增加使边坡自重增加；饱和地下水减小了岩土体的有效应力；含水率增加降低边坡岩土体的强度。在传统的极限平衡法里，水对岩土体有效应力的减小主要以水的静水压力分担了岩体正压力来表现。也有学者研究了含水率对黄土结构强度的影响的边坡稳定性[5]。还有对黄土边坡稳定性的影响[6]，对软岩边坡稳定性的影响[7]，对人工填土边坡的影响[8]。

本文把岩土体看作是符合Drucker-Prager破坏准则的理想弹塑性材料，仅研究由于含水率增加使岩土体强度降低，从而使边坡稳定性降低，确定满足边坡稳定要求的最大含水量。

1 问题的提出

中粉质土边坡高度为100m，边坡角为58°。求满足边坡稳定性要求的含水率。中粉质土的变形参数和密度见表1。

表1 岩土体物理力学参数

含水率对岩土强度参数的影响采用文献[9]的试验结果。研究结果见表2。

表2 控制含水率的直剪试验结果

粘聚力与含水率的关系如图1所示。内摩擦系数与含水率的关系如图2所示。

图1 粘聚力与含水率关系曲线

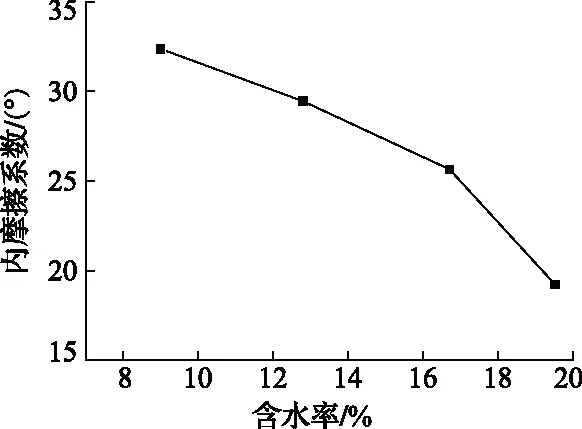
图2 内摩擦系数与含水率关系曲线

可见，粘聚力与内摩擦系数都是随含水率的增加而下降的。

2 计算原理

岩土体的含水率影响它的强度参数，因此，对不同的含水率，只要取对应的强度参数即可。采用参数测定时，进行排水慢剪试验，采用大变形的弹塑性有限元法模拟。在有限元计算过程中，两侧边界施加法向位移约束，底部边界施加全位移约束。

2.1 几何模型

边坡顶部水平方向、边坡底部水平方向及边坡深部都取边坡高度的3倍。计算几何模型如图3所示。

图3 单元划分与状态点

边坡高度方向均匀划分20个单元，边坡水平方向按等比数列划分成30个单元，最大与最小的比为4；边坡深度方向按等比数列划分20个单元，最大与最小单元的比为5；边坡下部水平方向按等比数列划分成20个单元，最大与最小单元的比为3。

2.2 失稳准则的选取

进入理想塑性状态后，材料从应力增量直接求应变增量的本构矩阵是不存在的。随着进入理想塑性状态区域的扩大，计算对象的有限元模型去掉刚体运动后的刚度矩阵也逐渐变得病态，直到接近奇异时计算无法进行。通常，这一状态对应计算对象的非稳定状态，因而被一些学者认为是计算对象达到了极限载荷，本文也采用这一准则。

2.3 稳定系数的选取

在边坡稳定性评价时，常见的稳定系数有两种给法：超载系数法和强度折减法。超载系数法是将载荷乘以一个数，使边坡达到临界破坏状态。强度折减法[10]是将材料的强度除以一个数，使边坡达到临界破坏状态，例如常用的刚体极限平衡法。超载系数法所乘的数或是强度折减所除的数都可作为稳定系数来衡量系数的稳定性。这里采用强度折减法。具体做法是选择F，按式(1)折减材料的粘聚力C与内摩擦角φ成为Cc与φc，并应用于计算中，使边坡处于临界失稳状态。此时，F称为稳定系数。

Cc=C/F，φc=arctan[(tanφ)/F]

(1)

2.4 塑性变形程度描述

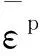
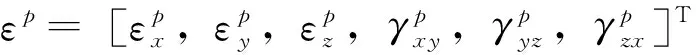
3 边坡的破坏模式

3.1 计算过程

按表2，选含水率为9%时的粘聚力122.77kPa与内摩擦角32.37°。计算步骤如下：

1)选择折减系数，按式(1)得到计算用的粘结力与内摩擦系数，并进行弹塑性计算。

2)如果计算不收敛，返回第一步，选择较小的折减系数；如果收敛，返回第一步，选择较大的折减系数，除非折减系数增加0.001后计算不收敛，则进行第三步。

3)此时得到的折减系数即为稳定系数。

经过反复试算，得到对应含水率为9%的稳定系数是1.577。

3.2 破坏模式

含水率为9%时按稳定系数折减加载过程各阶段塑性等效应变如图4—6所示。由图4—6可以判断边坡的破坏模式。图中的TIME值表示加载的完成率，SUB值是加载步的次序。

图4 按稳定系数折减时塑性区在坡脚处萌发

图4表明边坡破坏初期，塑性区首先在坡脚处萌生。坡脚处应力集中，在加载过程中率先进入塑性状态。

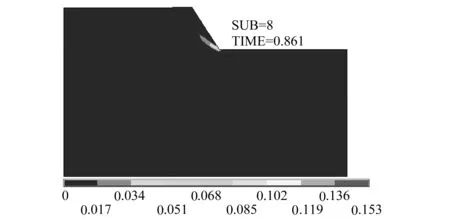
图5 塑性区按带状向坡顶方向扩展

图5表示，当重力加载进行时，塑性区从坡脚处开始，以带状向坡顶方向扩展。坡脚处的等效塑性应变始终是最大的。

图6表明，按稳定系数折减，在重力加载完成时，从坡脚萌生的塑性区已经扩展到边坡顶部，形成带状的贯通塑性区。这个塑性区可看作边坡潜在的滑带。

3.3 加载过程中边坡的塑性状态

取坡脚处率先进入塑性状态的231号节点(位置见图3)的等效塑性应变来表征边坡的塑性状态。边坡加载系数随这一塑性状态参量的变化如图7所示。

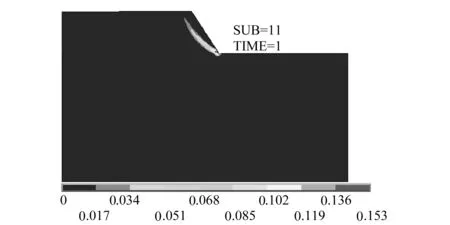
图6 含水率9%时强度折减到临界滑动的塑性区

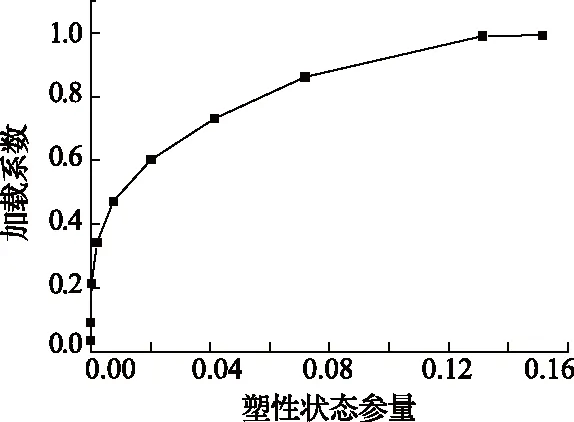
图7 加载系数与塑性状态参量曲线

可见，以稳定系数作为折减系数，当重力加载将要完成时，加载系数不再随等效塑性应变的增加而增加。此时塑性区已经贯通，塑性应变的增加不需要增加载荷。

4 含水率对边坡稳定性的影响

对表2中另外三种含水率情况也进行如上的分析。以各自的稳定系数作为折减系数，完成加载时的等效塑性应变如图8—10所示。可见，它们潜在的滑坡模式没有变化，仍然是条带状塑性区贯通的弧形滑动。

图8 含水率12.8%时强度折减到临界滑动的塑性区

图10 含水率19.52%时强度折减到临界滑动的塑性区

各种含水率对应的边坡稳定系数见表3。

边坡稳定系数与边坡含水率的关系如图11所示，可见含水率对边坡稳定性的影响非常显著，要使边坡的稳定系数不小于1.2，边坡的含水率不能大于13.8%。

表3 对应不同含水率的稳定系数

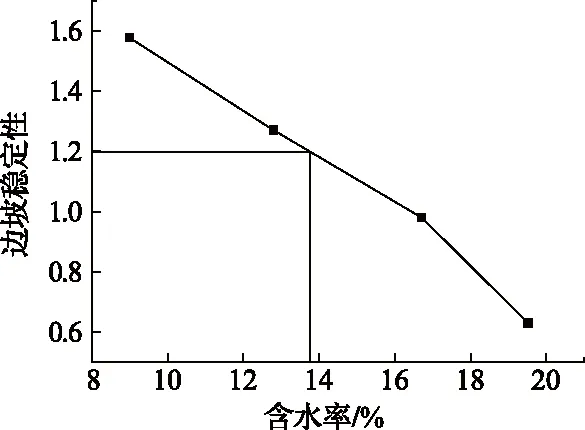
图11 边坡稳定性与含水率关系

5 结 论

1)边坡塑性区从坡脚萌生，随着重力加载进行，塑性区从坡脚以带状向坡顶方向扩展。这一带状塑性区贯通，形成滑坡体的滑面。这是滑坡的典型模式。

2)含水率提高使边坡岩土体的强度参数降低，进而降低了边坡的稳定性。边坡的稳定系数在一定含水率水平以下才有意义。

3)理想弹塑性有限元结合强度折减法和计算收敛性判据可以很好地给出一定含水率边坡的稳定系数。