高超声速飞行器空气舵系统耦合特性分析及颤振抑制研究

2019-02-19丁伟涛吴志刚黄玉平李建明

导弹与航天运载技术 2019年1期

丁伟涛，吴志刚，黄玉平，杨超，李建明

（1. 北京精密机电控制设备研究所，北京，100076；2. 北京航空航天大学，北京，100191）

0 引言

高超声速飞行器的舵系统是由舵机、传动机构与高超声速气动力、气动加热作用下的弹性舵面共同形成的耦合系统，存在着流、固、热、电、磁等多物理场的耦合作用。在一定的条件下，这种耦合可能引发颤振失稳，对飞行器的飞行安全产生严重影响[1]。

在颤振工程分析中，由舵面与舵机组成的舵系统一直是受关注的重点。在常规的舵系统颤振分析中，通常假设舵机为一个线性环节，其提供的支持刚度为一个常数。因此以线弹性元件来模拟舵机，其刚度值以舵面模态试验结果为依据调整得到。事实上，舵机本身是一个复杂动力学系统，其等效刚度是一个与频率有关的复数。此外在舵机内部和传动机构中存在着间隙、摩擦和死区等非线性环节，对舵系统颤振特性起一定的影响作用，可能使舵系统动力学响应呈现出极限环等非线性现象。因此常规分析模型不足以反映舵系统真实情况，需要更细致准确的分析模型。

目前国内外研究主要集中于气动力、热对于舵面颤振特性的影响方面，有关舵机动力学对颤振特性影响的研究鲜见于文章。Won-Ho等[2]对带有间隙环节和电动舵机的舵面进行了气动弹性分析，结果表明：考虑舵机动刚度与不考虑时计算得到的颤振速度和颤振频率均出现差别，而且非线性的影响会改变线性颤振特性，使得舵面出现极限环振荡现象。

本文主要针对热环境下舵面结构动力特性、高超声速非定常气动力、舵机环节非线性动力学特性耦合起来的舵机-舵面耦合系统颤振特性开展了研究，对舵系统耦合机理进行研究，建立了舵系统耦合数学模型，分析了热环境、舵机参数对舵系统颤振特性的影响，并提出通过电流环控制算法调节舵机动刚度相位实现提高舵系统颤振速度的方案，通过仿真验证了可行性。

1 舵系统耦合机理研究

采用电动伺服舵机的舵机-舵面耦合系统模型如图1所示。传统的舵面颤振工程分析是建立在将舵机环节根据舵面模态频率等效为弹簧模型的假设上，如图1a所示。实际上，电动舵机内部存在着转子的质量特性、阻尼特性等，在一定工作频率下，舵机动态特性不能简单地等效为弹簧[3]。

图1 舵面-舵机耦合系统模型示意Fig.1 Structure of Fin-actuator System Model

根据简化的电动舵机物理模型，电动舵机可以等效成一个单自由度的质量-阻尼-弹簧系统，如图1c所示，其运动方程表示为

式中 m为电动舵机等效转动惯量；c为电动舵机等效阻尼；k为电动舵机等效刚度；x为电动舵机角位移；f(t)为电动舵机输入转矩。

在式（1）中，舵机的刚度特性由电动舵机的电机力矩系数、位置反馈系数等参数决定，阻尼特性由转子阻尼、速度反馈系数等参数决定。在简谐运动中，电动舵机的角位移阻抗可表示为

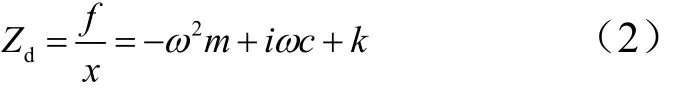
式中 ω为电动舵机角速度。

该位移阻抗即舵机动刚度（也称为复刚度），用下式表示：

式中 K 为复刚度 Z 的实部； K 为虚部； K eiφk

为 ZRdiAd的幅相表示形式，其中：KA为幅值，φK为相位。

由于舵机阻尼项的存在，舵机系统的回复力矩与转角运动之间存在着一定的相位差，即舵机动刚度是工作频率的复值函数。

为研究舵机动刚度的虚部对于舵面动力学特性的影响，以一个具有复数扭转刚度的简化舵系统为例进行定量分析，如图2所示。舵面假设为刚性，舵面考虑根部弯曲和根部扭转自由度，根部弯曲弹簧提供弯曲刚度 k1，扭转方向由舵机提供刚度 k2， k2是一个复

数， k2= KAeiφk，为分析简单起见，这里假设舵机动刚度为一个常数（即其幅值和相位均不随频率变化）。记舵面弯曲为第1阶广义坐标 q1，舵面扭转为第2阶广义坐标 q2，对应的质量特性为 Ixx（舵面弯曲惯量），Iyy（舵面旋转惯量）和 Ixy（舵面弯曲和旋转耦合惯量）。

该二自由度舵面的运动方程可以写为

式中1qF，2qF分别为第1、2阶广义气动力。这里采用一阶活塞理论计算舵面的非定常气动力，其上、下表面的压强差可写为其中，ρ为来流密度，c为来流声速，V为来流速度，z为舵面法向位移。设1φ，2φ分别为弯曲和扭转模态向量，则舵面弯曲和扭转模态对应的广义力分别为

式中1qWδ，2qWδ分别为广义坐标方向上的虚功。

式（4）最终形式为

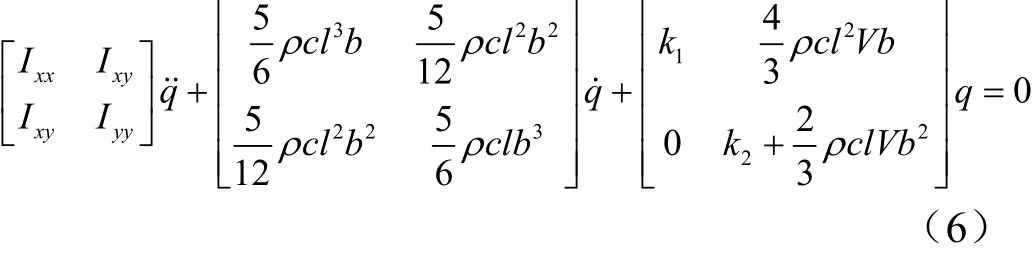
式中 b为舵面根弦半弦长；l为舵面展长。

对式（6）进行特征值分析，在给定的来流速度下求解特征值。当有一个特征值的实部由负变正时即为颤振临界状态，此时的来流速度即为颤振速度。经过对各种舵机动刚度幅值和相位角组合情况的计算，得到颤振速度和颤振频率，如图3所示。

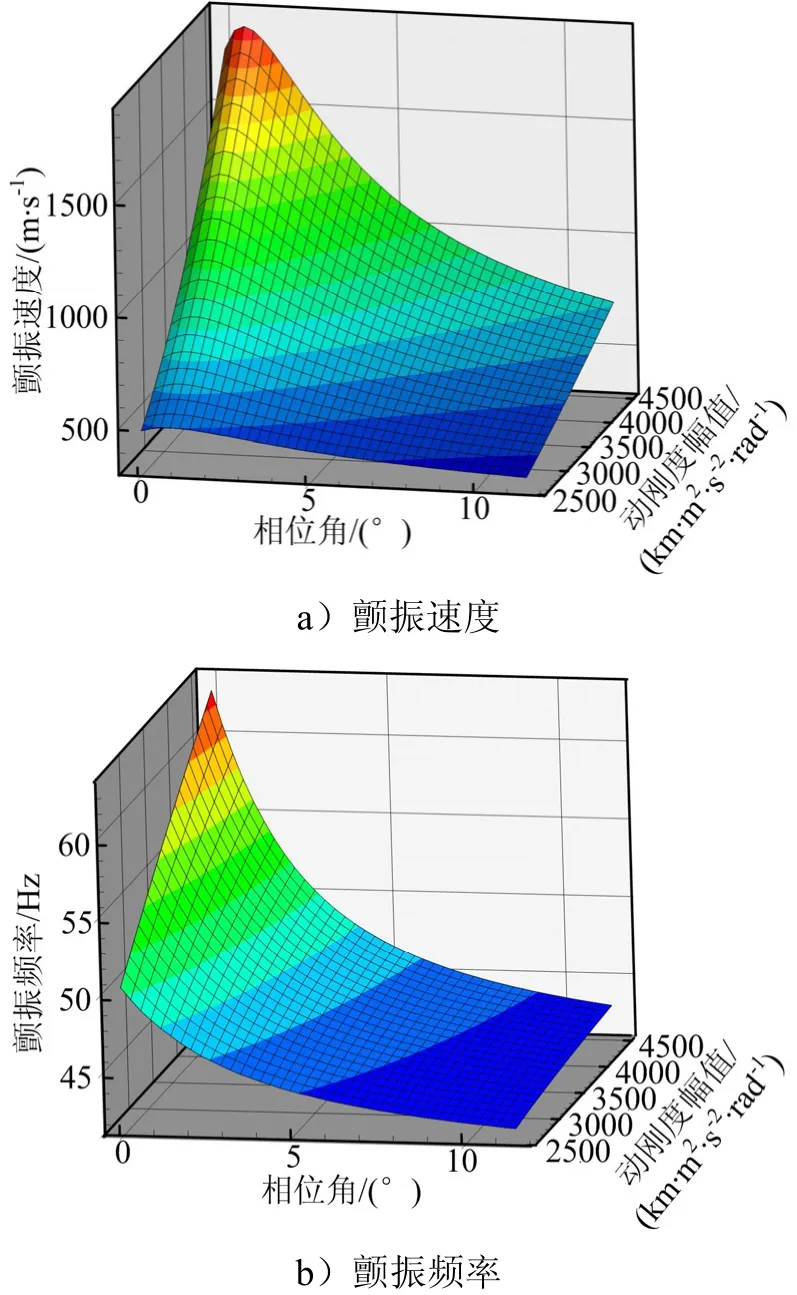
图3 简化舵系统颤振特性与舵机动刚度的关系曲线Fig.3 Relation of Simplified Actuator-fin System’s Flutter Characteristics and Dynamic Stiffness of Actuator

从图 3可以看出，舵系统的颤振速度随着舵机动刚度的幅值增大而增大，随着舵机动刚度的相位增大先略有增大然后大幅减小。由此可以得出，舵机动刚度的相位特性对舵系统颤振速度具有较大的影响。从另一方面看，如果能有效地调整舵机动刚度的相位，则在一定程度上可以改善舵系统的颤振特性，这为舵系统颤振抑制提供了一个新思路。

2 舵系统耦合数学模型

采用假设模态法[4，5]，舵面结构运动方程可写为

式中 M为舵面质量矩阵；x为假设模态坐标向量；Q(x，x˙，˙x˙)为气动力。对舵面取二阶局部刚化模态（舵轴弯曲θw和舵面扭转θt）和n阶根部固支弹性模态qi，即xT= [ q …qθ θ]。广义刚度矩阵K为对角阵，即1n w tK= d iag(k1， …，kn， kw， kt)。根据广义非定常气动力时域方程，式（7）转化为

将广义刚度矩阵K化为两部分，以便于将舵面扭转刚度tk单独分离出来，即：

式中tM为舵机对舵面施加的扭矩。式（10）可以简写为

式中fA，fB，fC分别为舵面状态空间形式的状态阵、输入阵和输出阵；tθ为舵轴输出转角。

对于舵机环节，可以根据舵机物理结构各环节运动方程得到舵机环节的动力学模型，它可以表示成如下非线性系统状态空间形式：

式中sx为状态量；tθ为舵轴转角，即舵机输入量。

舵机环节数学模型也可应用Matlab/Simulink软件建立时域仿真模型。利用力矩与转角的输入输出关系将舵面结构和舵机环节整合形成舵机-舵面耦合系统模型，在此基础上，采用数值积分法（如Runge-Kutta法）对耦合系统进行时域响应仿真分析，通过时域响应的收敛性来判断系统的颤振稳定性。

3 数值算例

3.1 舵系统颤振特性分析

利用 Matlab/Simulink软件建立舵机-舵面耦合系统的时域仿真模型，仿真初始时采用很小的阶跃力矩进行扰动，通过仿真分析得到系统的时域响应，通过响应曲线的收敛性来判断系统稳定性。高超声速飞行器飞行过程中，舵系统温度会随着时间不断升高，针对0 s（此时刻为常温）、500 s和2500 s 3种热状态进行舵系统颤振分析，得到颤振速度结果如表1所示。各热状态临界稳定时的舵面偏角响应曲线如图4所示。

表1 不同热状态的后缘舵系统颤振速度Tab.1 Actuator-fin System’s Flutter Velocity under Different Thermal Circumstance

舵机参数的变化对于舵系统颤振特性有较大影响，主要的影响参数为电机力矩系数 kt。保持电机力矩系数kt为0.3不变，改变线位移反馈比例系数，进行颤振分析，结果如表2所示。

表2 位移反馈系数对颤振速度影响（kt=0.3）Tab.2 Flutter Velocity under Different Position Feedback Coefficient（kt=0.3）

舵系统颤振速度同样受到指令信号幅值大小的影响。以阶跃指令信号为例，对舵机发出指令，指令幅值为1～5 V，颤振速度的变化如图5所示。计算模型采用热状态500 s时刻的舵面结构。

图5 舵系统颤振速度随指令信号幅值的变化Fig.5 Actuator-fin System Flutter Velocity Response of the Instruction’s Magnitude

前面的舵系统颤振机理研究表明，可以通过调整舵机动刚度相位来改善舵系统的颤振特性。这里提出在舵机电流环正向通道加入超前滞后环节(s + z) /(s + p)来调节舵机动刚度相位，在本文中的参数取值为p=145，z=515。颤振分析表明：以热状态500 s的舵面结构为例，在该组参数取值下，舵系统的颤振临界速度由原先的870 m/s提升到1380 m/s，颤振速度提高58%。图6给出了颤振抑制前后的时域仿真对比。

从图5中可看出，由于舵机环节中含有非线性因素，因此指令信号的幅值对舵系统颤振速度有很大影响，随着指令信号幅值的增加，颤振速度有较大程度的下降。