复合制导系统初始姿态安装一致性测量方法研究

王锴磊，冯伟利，崔桂利，王春喜

（北京航天计量测试技术研究所，北京，100076）

0 引 言

为满足新一代运载火箭的高可靠性、安全性及高准确度入轨的要求，采用两套或多套捷联惯组互为冗余的制导方式将成为制导系统的发展趋势[1]，并逐步采用捷联惯组/星敏感器复合制导方式。复合制导是在充分利用惯性导航系统的稳定性、连续性和抗干扰等特性基础上引进另一种类型的导航手段，对惯性导航系统的误差进行修正，从而获得更高精度的制导方案[2]。

在捷联惯组/星敏感器复合制导系统中，捷联惯组与星敏感器之间的初始姿态相对关系尤为重要，必须在火箭起飞前准确标定出二者之间的姿态关系，为后续导航和制导控制奠定基础。

目前，中国对于制导单元初始姿态的安装精度尚无有效的保障措施，初期是将两制导单元固联在同一结构强度好、尺寸庞大的基准板上，再将其整体在试验室测试，通过各制导单元自身的姿态角输出差值来完成其初始姿态的标定；然后整体运输到发射现场，安装在火箭上，给火箭带来上百公斤的多余负荷，既降低了火箭的有效运载能力，又无法实现现场快速标定。

本文提出的复合制导载体初始姿态测量方法基于非接触光电测角原理，待捷联惯组及星敏感器安装在仪器舱板上之后，通过相互对称的双路三维光电自准直测量系统，建立转换坐标系，准直制导单元的基准棱体进行准直测量，从而得出惯组和星敏感器基准棱体相对于中间转换坐标系的关系，解算出惯组坐标与星敏感器测量轴之间的初始姿态关系，实现复合制导载体之间初始姿态的现场测量。

1 测量数学模型

复合导航载体初始姿态安装一致性的测量，其核心是测量星敏感器和惯组之间的姿态关系。为了获取星敏感器测量坐标系与惯组测量坐标系之间的转换矩阵，需要建立一个过渡坐标系[3]，与两者均建立姿态关系，从而实现精确测量。基于设备的安放位置，建立如图1所示的测量模型。

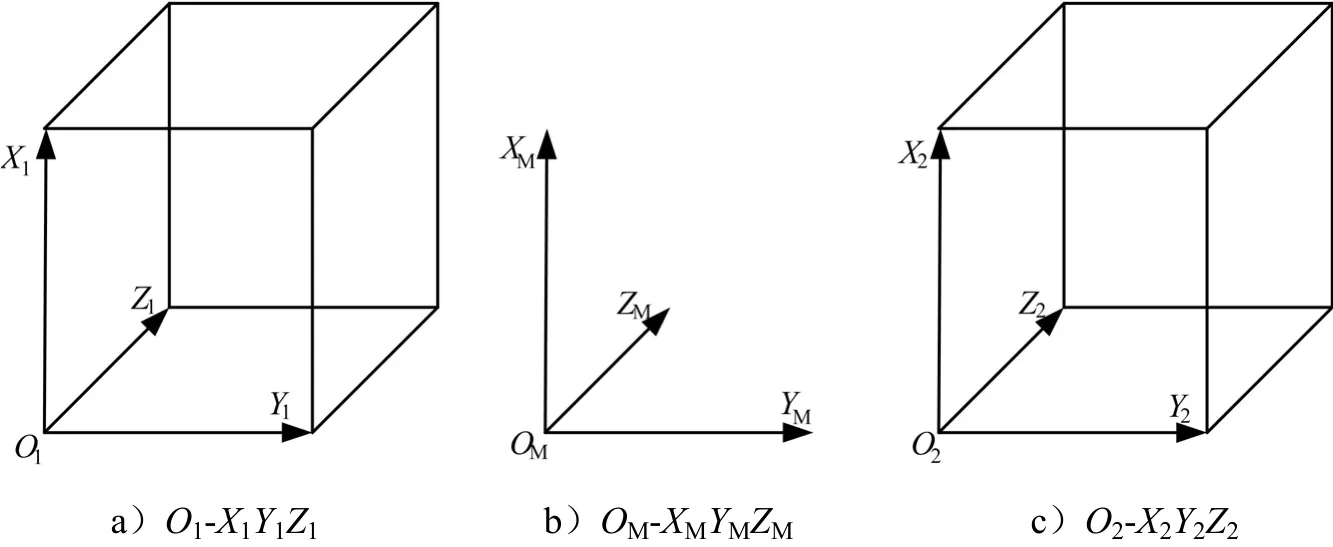
图1 校准装置测量坐标关系定义Fig.1 Definition of Measuring Coordinate Relation of Calibration Device

测量系统同时测量左右两侧立方体的3个角度，其中左侧角度定义为：

方位角γL：O1Y1在平面OMYMZM的投影与 OMYM的夹角，从 YM到 ZM为正。

俯仰角φL：O1Y1在平面OMXMZM的投影与 OMYM的夹角，从 XM到 YM为正。

滚转角ϕL：O1X1在平面OMXMZM的投影与 OMXM的夹角，从 ZM到 XM为正。

右侧角度定义为：

方位角γR：O2Y2在平面OMYMZM的投影与 OMYM的夹角，从 YM到 ZM为正。

俯仰角φR：O2Y2在平面OMXMYM的投影与 OMYM的夹角，从 XM到 YM为正。

滚转角ϕR：O2X2在平面 OMXMZM的投影与 OMXM的夹角，从 ZM到 XM为正。

姿态解算软件的基本功能是根据上述已知的6个数据求取坐标系 O1- X1Y1Z1与坐标系 O2- X2Y2Z2之间的关系。

设 O1- X1Y1Z1的基向量为 ex1，ey1，ez1；O2- X2Y2Z2的基向量为 ex2， ey2， ez2; OM-XMYMZM的基向量为 exM，eyM， ezM；因此定义：

利用MATLAB软件求解上述方程，可得出两个坐标系之间的转换矩阵。

2 测量装置搭建

由图1可知，为了实现系统初始安装姿态的一致性测量，需要精确的Lγ，Lφ，Lϕ，Rγ，Rφ和Rϕ。而惯组和星敏感器中，由基准六面体表征其安装姿态，这几个角度也就是基准六面体所表征的角度。利用自准直光电测角技术实现每一个基准六面体的非接触测量，其基本测量原理如图2所示。

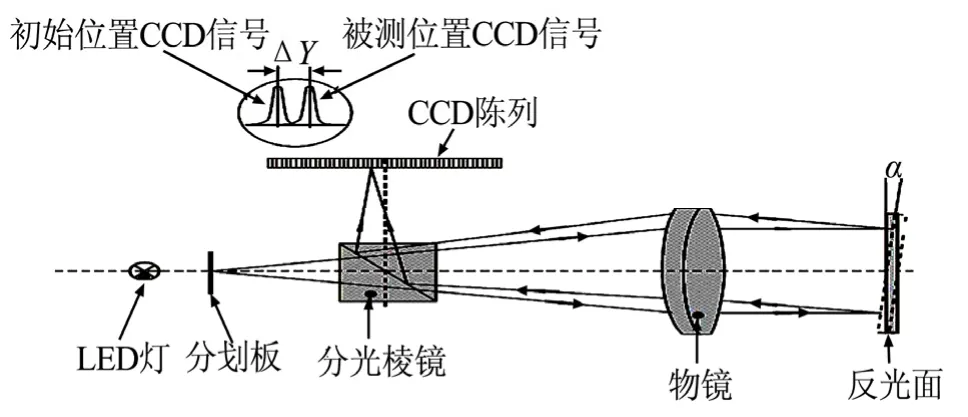
图2 自准直测量原理示意Fig.2 Principle of Self Collimation Measurement ΔY—初始信号与被测信号之间的距离

由图2可知，LED光源均匀的照射在分划板上，形成一条均匀的测量狭缝。分划板放置在光学系统的焦面上，经过物镜后以平行光的形式投射在被测反射镜上，该反射镜将其光束反射在自准直仪内部经过分光镜在CCD上形成图像，如果反射镜与自准直仪的主光轴垂直则自准直光束原路返回。当反射镜变化 α角时，其反射光束就以2α的角度返回，根据反射光束的倾斜程度会在CCD上的不同位置产生图像，并根据三角函数原理计算测量角度α[4]。

通过CCD测量YΔ即可知道被测反射镜偏转的角度。基于以上分析建立空间正交的多通道测量系统实现Lγ，Lφ，Lϕ，Rγ，Rφ和Rϕ的精密测量。双路三维光电自准直系统利用其两两对称布置的4条自准直光路，分别对准捷联惯组和星敏感器上两个基准棱体上的侧面和顶端反射基面。每一维自准直光路对准各自的基准棱体反射面，并保证相对应的两条光路同轴，即绝对零位一致。每条自准直光路的出射光线经基准棱体反光面反射后，返回光线与其零位光轴发生角度偏移，依此测量对应角度。依此类推，同样可以得出其它两个方向上的角度，从而实现对复合制导系统初始姿态三维角度进行测量。其基本的测量模式如图3所示。

图3 校准装置姿态测量模式示意Fig. 3 Attitude Measurement Mode of Calibration Device

按照图3的测量模式，建立如图4所示的测量光学系统。本装置的光学系统由4条光电自准直光路组成。其中，自准直光路1和4构成测量装置的左侧测量光轴，完成捷联惯组基准棱体3三维姿态角的测量，自准直光路2和5构成测量装置的右侧测量光轴，完成星敏感器基准棱体6三维姿态角的测量。自准直光路1、2的准直分划板经过物镜射出平行光束，再经五角棱镜转向后射向基准棱体的顶部反光面，完成基准棱体在滚转方向上相对自身零位光轴偏转角度的测量。自准直光路4、5为双线阵CCD光电自准直光路，完成基准棱体在偏航和俯仰两个方向上相对自身零位光轴偏转角度的测量，由此实现6个测量通道完成Lγ，Lφ，Lϕ，Rγ，Rφ和Rϕ的精密测量。

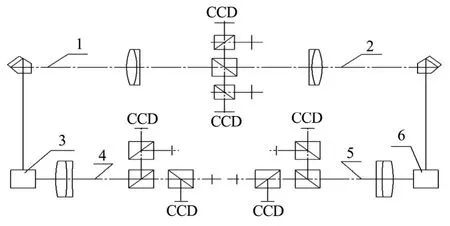
图4 测量光学系统示意Fig.4 Measuring Optical System 1、2、4、5—自准直光路；3—星敏感器基准六面体；6—惯组基准六面体

主机基体是测量光学系统和 CCD光电测角接收单元的载体，是测量装置的测量准确性的保证。由于进行现场测量，因此对主机基体的选材和结构进行优化设计，在提高基体的刚度同时，保证基体的质量不能太重。

主机材料选取优质铸造铝合金材料，结构采用T形框架式结构，在基体的侧壁上设计有加强筋，保证基体具有较好的结构强度。其结构外形如图5所示。

图5 主机基体结构示意Fig.5 Matrix Diagram of Main Engine

控制系统是基于 CCD图像处理技术的原理来设计的。将CCD所采集到的表征光学信号的电信号进行数字化处理，通过软件对每一个像元的参数进行分析评估后进行二值化处理，得出该像元所代表的真实的光学信号，从而准确地得出CCD所表征的真实的位置变化，进而对被测物体进行准确评估。

自准直仪的角度测量是通过对 CCD每一个像元的分析得出光照的重心位置，从而确定光照位置的位移。该自准直测量系统完成双轴的测量，因此，控制系统需要分别对两轴的测量数据进行实时采集和评估，完成双通道同步测量，其控制原理如图6所示。

图6 控制系统原理框图Fig.6 Block Diagram of Control System

按照上文所述的测量原理、光学、结构和控制系统设计方法，设计了如图7所示的测量系统，该系统建立了自身测量坐标系，基于非接触的自准直测量原理实现两个坐标系之间姿态关系的测量。测量范围在各个方向均可达到1000″。该测量系统经过试验室的测量验证和实际使用，完全满足复合导航载体初始姿态安装一致性的测量。

图7 姿态一致性测量系统示意Fig.7 Attitude Consistency Measurement System

3 测量结果验证分析

3.1 验证测量方法

以两个标准六面体为被测目标，首先利用该设备测量其相互之间的姿态关系，其中一个标准六面体放置在三轴转台上，另外一个标准六面体放置在平板上，通过电子经纬仪建立坐标系，测量两个六面体的初始姿态，使其保持一致；然后调整三轴转台，带动六面体旋转，使其3个方向均有角度产生，以三轴转台的输出为标准，验证该方法和装置的测量结果。

3.2 测量数据分析

依照上述方法，在试验室对测量数据进行了测试，测量数据如表1所示。

表1 试验室验证测量数据Tab.1 Test Data Validation

验证测量误差时，在其测量范围内进行了10次测量，以转台的姿态角输出为基准，10次的最大测量误差不超过3″，整体性能满足设计要求。对主要误差源从以下几个方面进行分析：

a）光机结构的制造误差主要包括透镜的焦距误差和透镜的偏心差。此项误差是零件加工时的保证。为了减少对测量系统的影响，在进行光学成像系统设计时合理提高技术指标的要求，可在加工时保证透镜的加工满足设计要求。

b）由于光电转换的不均匀性和非线性，使线阵CCD的输出信号不能真实地反映曝光量的分布。曝光量分布的失真，使提取的特征信号发生失真，其结果将导致测量误差。

c）本装置的三维姿态角偏差测量，需建立3组两两相对应的测量光路，每一组相互对应的测量光路分别完成每一维角度差的测量。由于对应的两路准直测量系统相互独立，因此应具有各自单独的绝对零位。为了消除两测量光轴的初始零位不一致所产生的测量误差，这就要求每一组相互对应的测量光轴严格同轴，也就是初始零位相同。

3.3 测量不确定度评定

以方位角测量为例进行不确定度评定，依据测量方法建立不确定度评定数学模型[5]，即：

式中 β为被测角度值偏差；α为被测的任一位置角度值；s为标准角度值。

测量不确定度的因素如下：

a）三轴转台测量误差引入的不确定分量1u。

由于测量系统以三轴转台的姿态角输出为基准进行测试，其测量不确定度U=1.0"，则：

b）光电自准直系统单轴综合测量误差引入的不确定度分量 u2。

测量系统中测角系统的综合测量误差是对每个轴单独进行标定，每个轴所产生的测角示值误差最大值为 Δ δmax= 1 .2"，按正态分布，查表得置信因子k = 2 .58，故引起的不确定度为

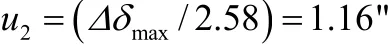
c）零位光轴的稳定性引入的不确定度分量3u。

测量系统中每一条光路均有自己的绝对零位，故零位光轴的变化将带来测量误差，其中单路绝对零位最大变化为maxε1.2"=， 因此相对应的两路绝对零位变化引起的不确定度为

d）两对应光轴之间零位光轴的不重合误差引入的不确定度分量4u。

两光轴之间零位光轴的不重合所产生的误差为λ 0.6"= ，取均匀分布，置信因子k 3= ，其引起的不确定度为

e）测量重复性引入的不确定度分量5u。

单通道测量系统的测量重复性ω 0.3"= ，取均匀分布，置信因子k= ，其引起的不确定度为

式中 U为扩展不确定度；k为包含因子。

4 结束语

复合制导系统是运载火箭今后的主流导航方式，本文基于坐标变换的原理建立测量模型，基于非接触的自准直测角原理实现姿态角的测量，实现了复合导航载体初始姿态安装一致性的测量，经过试验室验证和现场测试，达到了测量效果，具有较高的推广应用价值，在今后的系统改进设计中，降低系统质量，提升系统采样速度和测量可靠性将是改进研究的重点。