基于算法优化的中国高速动车组车外噪声源识别研究
2019-02-18李晏良李志强何财松陈迎庆
李晏良,李志强,何财松,陈迎庆
(中国铁道科学研究院集团有限公司 节能环保劳卫研究所,北京 100081)
引 言
随着计算机存储和运算性能的大幅提高,多通道的声阵列技术已经成为复杂噪声源识别的主要手段。利用声阵列技术进行噪声源识别主要有近场声全息法[1-5]和波束形成法[6-8]。近场声全息法利用声场空间变换算法,要求阵列不能离噪声源太远,且阵列孔径需要与声源大小相当,阵元最小间距与识别频率上限的半波长相当,从安全性和经济性考虑,不适合用于高速动车组噪声源识别;波束形成技术不受声源数目限制,且识别范围具有一定张角,阵列孔径可以小于噪声源尺寸,是国内外高速动车组车外噪声源识别的主要方法[5-13]。在高速动车组车外噪声源识别研究方面,目前国内外各研究机构利用波束形成技术,均识别出了车体下部的转向架区域、受电弓区域等是高速动车组的主要噪声源位置,同时得到车体空气动力噪声和集电系统噪声所占的比重随动车组速度提高而升高等结果[9-13]。但从已发表的识别结果[9-13]来看,识别精度受运动声源多普勒效应引起的噪声信号频移及频带扩展和传声器阵列波束旁瓣引起的虚假声源两方面的影响,既有识别结果均存在着分辨率较低、部分区域虚假声源较多等问题,这不仅影响对噪声源频率特性和产生机理的判断,也导致噪声源区域划分不准和噪声源贡献声功率的比例计算偏差大。
针对运动声源的多普勒频移问题,莫尔斯[14]早已推导出声源在亚声速运动时静止接收点的信号特征,杨殿阁[2,4]在此基础上通过将其与声源和接收点相对静止时接收点的噪声信号对比,得到了对静止传声器接收到的声信号去多普勒效应的校正公式,刘方[15]基于该方法开展试验测试,对校正前后信号的频谱与实际噪声源进行对比分析,证明该方法有效可行。针对传声器阵列波束旁瓣引起的虚假声源的问题,目前清晰化声源识别图像、降低旁瓣干扰的方法有声源成像反卷积方法(DAMAS)[16]、扩展的声源成像反卷积方法(DAMAS2)[17-18]、非负最小二乘法(NNLS)[19]、基于快速傅里叶变换的非负最小二乘迭代反卷积法(FFT-NNLS)[20]、清除法(Clean)[21]、基于同一声源产生的主瓣与旁瓣相干的清除法(CLEAN-SC)[22]等,国内外学者利用单个点源、多个不相干点源和多个相干点源开展了仿真和试验对比,根据对比结果,FFT-NNLS计算速度相对较快,且对不相干点源和相干点源均有相对更好的识别结果,适合应用于复杂噪声源的识别[23-25]。
本文利用多普勒效应校正公式和FFT-NNLS算法对传统的波束形成算法进行优化,并利用优化后的算法对应的测试边界条件,合理设计试验方案,开展了我国某型动车组噪声源识别试验,获得与以往噪声源识别结果相比分辨率更高、定位更准确的结果。同时根据噪声源垂向分布情况,合理划分噪声源区域,计算并分析了不同区域噪声源的声功率占比和频率特性。
1 波束形成算法优化
1.1 多普勒效应消除
依据多普勒效应,当声源和受声点发生相对运动,在声源由远处驶向受声点时,受声点传声器接收到的频率大于实际声源频率;当声源驶离受声点时,受声点麦克风接收到的频率小于实际声源频率。如图1所示,一辐射噪声频率为f0的噪声源,在t=0时刻,从A点以恒定的速度V向B点运动,受声点位于O点,经过时间t1,声源到达B点,同时辐射出相位为φ的声波,θ为BO与运动方向的夹角。又经过时间t2后该相位的声波波阵面到达受声点O,传播路程为BO的长度R(t),则受声点O在t时刻接收到的由声源在t1时刻辐射出的相位为φ的声波频率fr0为
(1)
式中:c为空气中声速;M=V/c为马赫数。
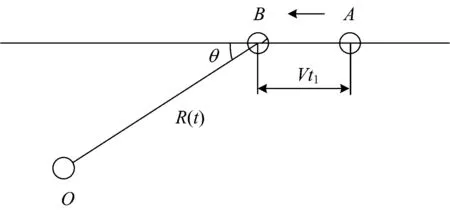
图1 多普勒效应示意图
由于声源的位置随时间会不断变化,因此受声点的信号频率也随声源位置变化而变化,当声源靠近受声点时信号频率大于实际频率并随距离减小而减小,当声源远离受声点时接收信号频率进一步减小,因此受声点最终得到的是在实际信号频率附近发生频带扩展后的信号。根据莫尔斯运动声源的理论,假设声源为小球声源且传播过程中没有能量损耗,则从声波方程和相对运动关系出发,可得传声器测量到的声压信号可以表示为[14]
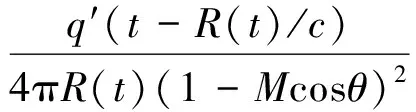
(2)
式中:q(t)=q0ejw0t为声源的体积变化速度;q0为声源体积变化速度幅值,即声源强度;w0为声源辐射噪声角频率;q′(t)为q(t)对时间t的一阶导数,即q′(t)=dq(t)/dt。
式(2)的第1项为声压按照1/R(t)减小的辐射场,当R(t)距离较远时,第2项与第1项相比为小项,可以忽略[4],则式(2)所示的传声器测得的声压信号近似表示为
(3)
假设存在另一传声器,在t时刻与声源距离为r时以相同的速度运动,此时声源和传声器没有发生相对运动,则马赫数M=0,此传声器接收到的噪声信号为无多普勒效应的噪声信号,该传声器接收到的噪声信号pr为
(4)
式中:k0=w0/c,为波数。
将式(3)进行换算,并代入式(4),整理可得

(5)
因此,当传声器与声源距离满足远场条件时,如果已知数据采集某时刻对应的声源与传声器的相对位置、声源的运动速度,即可对传声器采集到的信号进行去多普勒效应的校正。
1.2 基于快速傅里叶变换的非负最小二乘迭代反卷积
传统延迟求和波束形成输出结果是声源分布与阵列点传播函数(array’s point spread function, psf)的卷积,受阵列孔径的有限性和采样点离散性的影响,阵列点传播函数在不同频率具有不同的带宽,同时在主瓣两侧会出现旁瓣及栅瓣,这些不利因素会使基于传统的延时求和算法得到的声源识别图像出现阴影或虚假声源,从而影响了声源识别的准确性。如图2所示是传统波束形成算法得到的我国某型号动车组受电弓车的噪声源识别云图,受阵列波束的旁瓣和栅瓣的影响,相邻各噪声源的声强云图互相弥漫,且在没有明显噪声源的位置有较多的虚假声源,噪声源识别的精度不足。

图2 传统波束形成算法的噪声源识别结果(声强级)
FFT-NNLS算法假设阵列共有N个传声器,第m个传声器的坐标向量为rm,且假设噪声源均位于与阵列平面平行的一个矩形平面上,对这一矩形平面划分计算平面焦点网格,计算平面内网格点坐标向量为r,阵列中各传声器同步采集声信号,并反向聚焦各网格点,得到输出量如下式所示。
(6)
式中:b(r)为未标准化的输出量;C为阵列传声器接收声信号的互谱矩阵;1为元素均为1的矩阵;v=[vm(r)]为r聚焦点的转向列向量;w(r)=[|vm(r)|2]。
(7)
假设各声源互不相干,声源坐标为r′,r′处的声源强度为q(r′)则各传声器接收信号的互谱为各声源分别在阵列传声器处产生信号的互谱的和,即
(8)
将式(8)代入式(6)可得
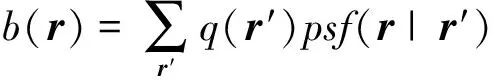
(9)
式中:psf(r|r′)为阵列点传播函数,表示r′的单位强度声源对r聚焦点的贡献量。
对阵列点传播函数做空间快速傅里叶变换,得到波数域形式PSF。
PSF=F[psf]
(10)
式中:F[]为快速傅里叶变换算子。
在波束形成输出结果、阵列点传播函数和声源分布之间建立式(11)的差函数φ,通过最小化该差函数来求解声源强度分布q。
(11)
式中:A为阵列点传播函数的矩阵;b为传声器阵列中各传声器实测的输出结果的矩阵。
初始化q(0)=0, 采用梯度投影法反复迭代n次搜索来获取q(n),在第n次迭代计算结果到第n+1次迭代计算结果的步骤如下。
(1)计算残差向量,计算公式为
r(n)=Aq(n)-b=F-1[F[q(n)]PSF]-b
(12)
式中:F-1[]为快速傅里叶逆变换算子。先通过傅里叶变换算法,将式9中第n次迭代得到的声源分布与阵列点传播函数的卷积转换为波数域的乘积以减少计算量,之后再进行傅里叶逆变换得到Aq(n)。
(2)计算φ关于q的负梯度向量w(n),计算公式为
w(n)=-ATr(n)
(13)
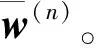
(4)计算辅助向量g(n),计算公式为
(14)
(5)计算最优搜索步长λ,计算公式为
(15)
(6)确定q(n+1),计算公式为
(16)
当次数n足够大时,得到的q成像结果与实际声源相近,显著提高声源识别的分辨率。
2 动车组车外噪声源识别试验
2.1 测试方案
根据高速铁路噪声频率特性,设计了满足高速动车组车外噪声源识别需求的爪形阵列,该阵列由11个长度为1.8 m的轮辐组成,每个轮辐上有6个间距不等的传声器。该阵列在低于350 Hz时不出现旁瓣,在400 Hz时主瓣级与最大旁瓣级差大于20 dB,在1 000 Hz时主瓣级与最大旁瓣级差为14.4 dB,在5 000 Hz以内主瓣级与最大旁瓣级差不小于10.0 dB。图3给出了该阵列在1 000及4 000 Hz频率处的阵列点传播函数图像。
基于优化后的波束形成算法,选择典型桥梁线路区段,开展我国某新型动车组噪声源识别试验,试验现场布置示意见图4。试验动车组总长度209 m,升弓高度5.3 m,采用4动4拖的8辆编组方式,车头及车顶分别采用流线型和平顺化设计,空调及受电弓设备沉入车顶以下。测试区段桥梁类型为32 m简支箱梁,梁面宽12 m,防护墙高度为0.7 m,轨道类型为CRTS Ⅰ型双块式无砟轨道,并采用WJ-8型扣件以及60 kg·m-1标准轨。
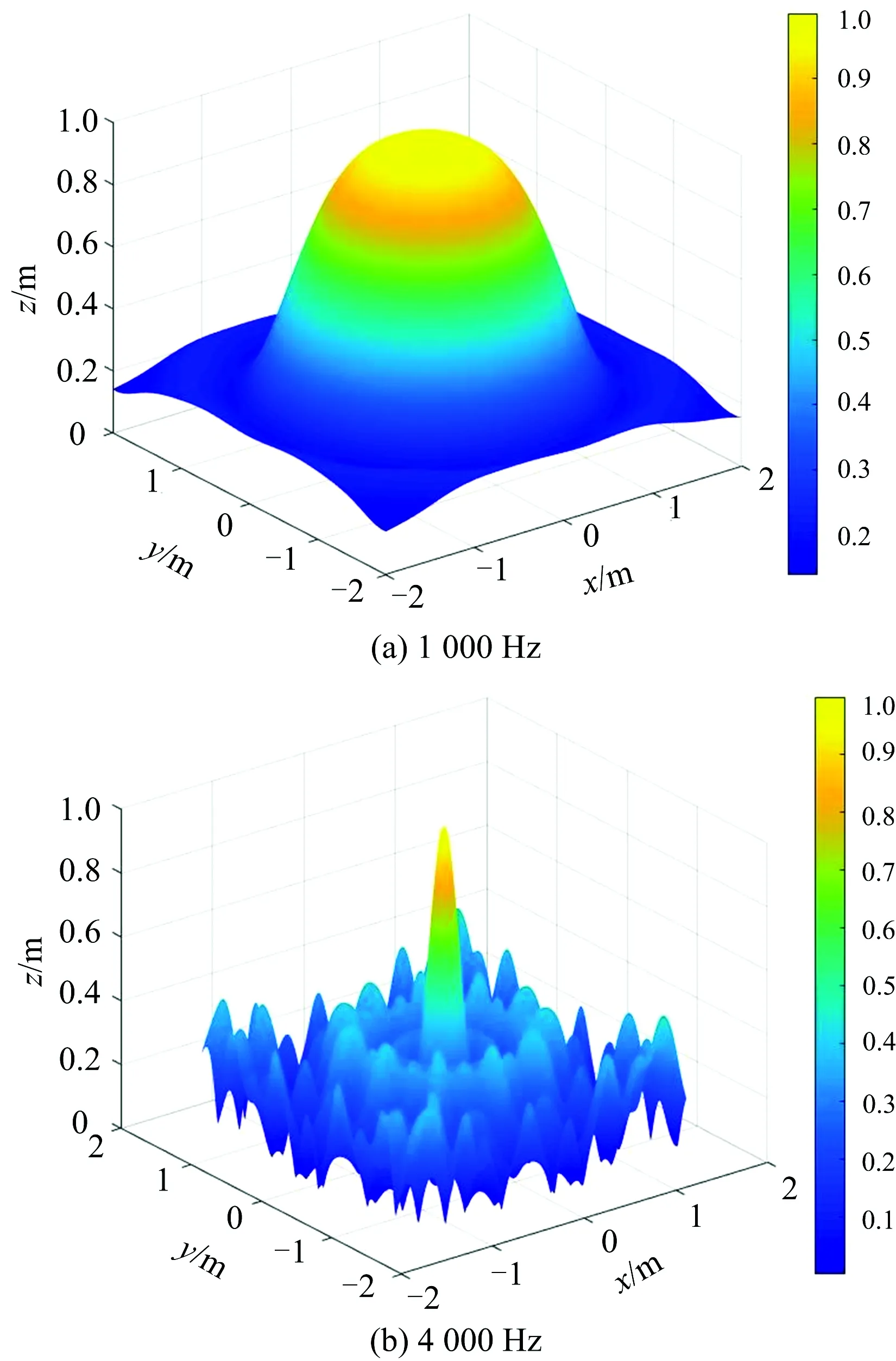
图3 爪型阵列点传播函数图像

图4 试验现场布置示意图
2.2 测试结果
2.2.1 主要噪声源分布
本次试验获取了动车组从低速到350 km·h-1各速度级的噪声源分布,图5为动车组以350 km·h-1速度运行时的噪声源识别结果(计算频率范围为200~5 000 Hz)[27-28]。与国内既有的噪声源识别结果[13,24-26]相比,本次试验得到的声源识别结果有效抑制了旁瓣干扰,分辨率大幅提高,且噪声源定位准确,动车组高速运行时的主要噪声源声强级云图均准确识别于相应的声源位置,各噪声源边界清晰,相互之间的弥漫性干扰得到有效消除。
图5 动车组以350 km·h-1速度运行的声源识别结果(声强级云图)
由噪声源声强级云图分布可知,动车组高速运行时,受电弓、转向架和头车排障器等区域是噪声主要来源。350 km·h-1时最大声强级位于受电弓升弓区域,且从接触网至车顶声强级均较高,说明受电弓的弓形滑板及弓臂会产生较大的空气动力噪声。而在受电弓降弓区域,由于受电弓沉入车顶以下,与升弓区域相比噪声小很多。
车辆下部区域,从头车排障器至尾车最后一个转向架,分布大小不等的噪声源,其中以转向架区域的噪声更为明显和集中。转向架区域噪声主要包括轮轨滚动噪声和各部件引起的空气动力噪声,虽然声强级小于受电弓升弓区域,但由于噪声源数量多,总的声能量要远大于受电弓区域。此外,头车排障器区域和第1转向架区域存在强烈的空气动力噪声,除头车第1转向架区域外,各拖车转向架区域声强级均小于动车转向架区域声强级。
车体区域噪声云图不明显,说明车体区域声强级与受电弓升弓区域相比小10 dB以上(噪声云图动态显示范围设为10 dB)。车体区域噪声源主要为空气动力噪声,近几年主机厂在车体流线型设计和平顺化设计方面做了大量工作,包括车体表面局部区域和车头风挡区域低流阻、低噪声优化等,车体区域空气动力噪声显著减小。
2.2.2 主要噪声源垂向分布占比及频率特性
对动车组噪声按照垂向分布情况进行划分,计算不同高度范围内声功率占比,分析噪声频率特性。表1为本次试验动车组噪声垂向划分区域,由下到上依次为下部区域、车体区域和受电弓区域。

表1 动车组噪声垂向划分区域
动车组以200,250,300和350 km·h-1等典型速度运行时垂向不同区域声功率占比见图6。动车组速度由200 km·h-1提高到350 km·h-1时,下部区域声功率占比由91.3%降低至78.9%,车体区域由6.5%升高至11.5%,受电弓区域由2.2%升高至9.6%。随着车速增加,以空气动力噪声为主要声源的车体区域和受电弓区域声功率占比增大,但350 km·h-1速度时车辆下部区域噪声依然占据绝对主导作用,因此应特别加强下部区域噪声特别是轮轨区域噪声的控制。
动车组以300和350 km·h-1速度运行时总声功率及垂向不同区域声功率的频谱特征见图7(图中纵坐标C的值为某基准值)。可以看出,受下部区域噪声占比较高的影响,总声功率与下部区域噪声声功率的频谱曲线较为接近,主要噪声在为500~1 000 Hz频段,轮轨相互作用噪声频率特性明显。车体区域噪声在中心频率为315 Hz的频段声功率级较高;受电弓区域噪声主要位于250~630 Hz的低频段,且以中心频率为315 Hz的低频噪声为主。车体区域和受电弓区域的噪声为典型的空气动力噪声。

图6 不同速度下动车组各区域声功率占比(桥梁测试区段)
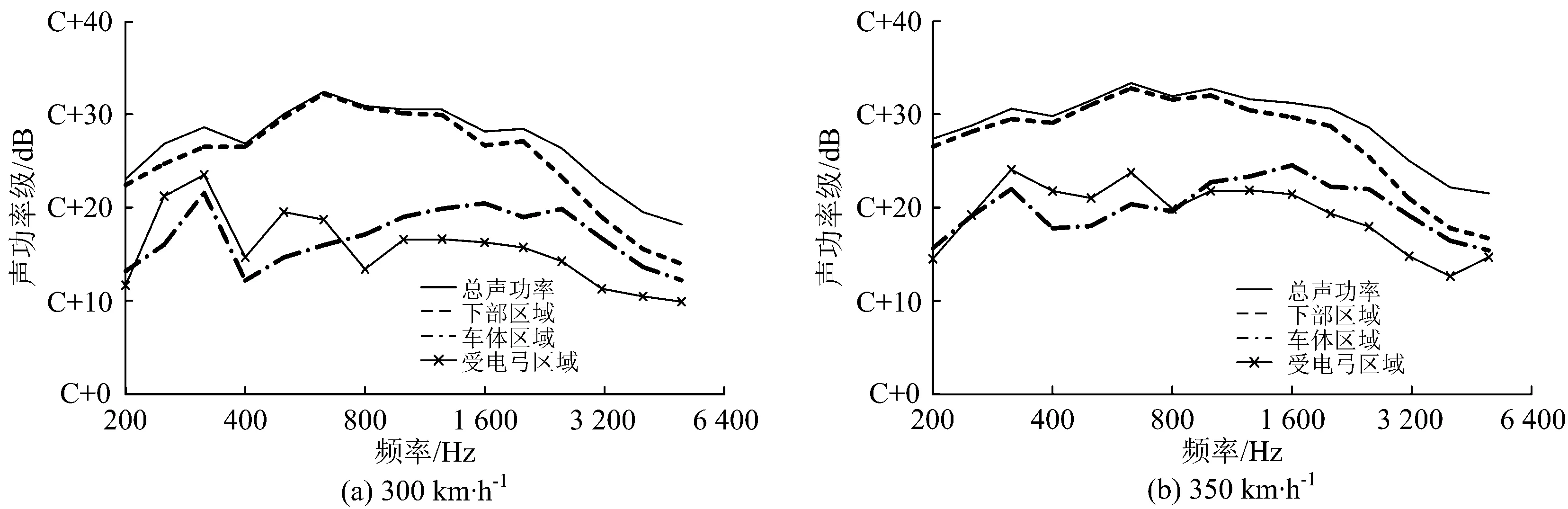
图7 300和350 km·h-1速度下动车组不同区域声功率频谱特征
3 结 论
(1)为提高运动声源噪声源识别的准确度,本文对传统声源识别波束形成算法进行基于快速傅里叶变换的非负最小二乘迭代反卷积 (FFT-NNLS)和多普勒效应时域修正算法的优化,并设计出一套适合应用于高速铁路噪声源识别的高性能传声器阵列,实现了对高速铁路噪声源精准定位和定量识别。
(2)声源识别结果表明,动车组车外噪声源主要分布于转向架区域、头车排障器区域、受电弓升弓区域等处;各噪声源声强级和声功率级随速度变化规律及频谱特征均反映了下部区域噪声源主要为轮轨滚动噪声源;头车排障器区域及车体区域的噪声源为典型的单极子空气动力噪声源,受电弓区域噪声源为典型的偶极子空气动力噪声源。
(3)动车组以350 km·h-1及以下速度运行时,下部区域依然是噪声贡献量最大的区域,占70%以上(桥梁测试区段),且以轮轨滚动噪声为主。因此,动车组下部区域噪声是高速铁路噪声控制需要重点关注的区域。
