基于偏置伽马分布的高速铁路地震预警及紧急处置时延特性分析
2019-02-19戴贤春习年生
王 澜,戴贤春,习年生
(中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心,北京 100081)
对于高速铁路而言,地震是危害性极强的自然灾害,会直接破坏铁路基础设施,也会导致运行列车脱轨、倾覆等重大事故。有效的高速铁路地震预警及紧急处置措施,可使列车在地震灾害发生时的损失程度降至最小。随着我国高速铁路运营里程的增加,地震危害的潜在风险越来越突显,对地震预警系统的实时性要求也随之越来越高[1-2]。
研究适合我国高速铁路技术特点与实际需求的地震预警及紧急处置理论与方法,提高地震紧急处置的实时性,以确保高速铁路行车安全和减轻地震次生灾害,是急需解决的关键科学问题[3-4]。
日本新干线早在1978年开始进行地震P波预警,这套系统称为早期地震检测警报系统(UrEDAS)[5]。该系统采用触发接触网断电方式进行地震紧急处置,并利用ATC车载装置监测接触网带电状态,当监测到接触网失电后触发列车制动系统动作。接触网失电至列车开始制动的时延约为4 s。2007年后,JR东日本在高速列车上加装了专用接触网带电状态检测装置,该装置当检测到接触网失电后直接控制列车制动系统实施制动,从而,将接触网失电至列车开始制动的时延缩短到约3 s[6]。
法国高速铁路地中海线和我国台湾高速铁路均装备了地震监测报警系统。该系统当检测到破坏性地震波到达后将警报信息由控制中心发送给ATC列控系统,控制列车制动停车[7]。控制中心发出警报信息至列车开始制动的紧急处置时延约为5 s。
我国新研发的高速铁路地震预警系统采用P波预警方式,即根据地震台站实时测定的地震P波初至信息快速估算的地震动参数确定地震影响区域及其警报等级,在破坏性地震波到达之前,向地震影响范围内的本地及异地铁路发布地震警报信息。地震紧急处置采用多路径方式,即由地震预警监测铁路局中心系统向高速铁路相关系统发布紧急处置信息,联动触发牵引供电系统断电、列控系统控车、通信系统向车载地震紧急处置装置(简称“车载装置”)发送信息,控制高速运行的列车减速或紧急制动停车。通过这样的措施以保证列车运行安全。
地震预警时延[8-9]主要指首台站P波初至到地震预警监测铁路局中心系统发出地震警报首报信息的时间差。该时延包括:滤波、数据采集及打包、数据处理、预警决策分析、数据发送、信息排队与传输等时延。
地震紧急处置时延则为铁路局中心系统发出紧急处置信息到地震影响区域内运行的高速列车开始采取减速或紧急制动措施的时间差。该时延包括:信息打包、信息发送、信息排队、信息传输、信息处理、继电器动作、系统响应等时延。
地震预警及紧急处置的时延越小,表明系统实时性越好。这对于破坏性地震波到达高速铁路沿线之前有充分的时间提前采取有效的紧急处置措施,以减轻或避免地震灾害损失十分必要。
受高速列车紧急制动试验条件限制,很难获取高速列车紧急处置大样本统计数据。因此,本文基于地震预警大样本统计数据和紧急处置有限样本统计数据,在分析不同时段的时延特征和概率分布模型的基础上,建立总时延的偏置伽马概率分布模型,从而获取更高置信度的高速铁路地震预警与紧急处置总时延的分布特性与规律,以便进行综合比较与评价。
1 地震预警及紧急处置时延模型
1.1 偏置伽马分布模型
地震预警及紧急处置时延在不同的条件下受大量不确定性因素影响,可能取各种不同的值,具有不确定性和随机性,但这些取值落在某个范围的概率是一致的,具有统计规律性。高速铁路地震预警时延宜采用随机变量函数模型进行描述,且具有单边、连续性、不对称型随机变量分布特征。
实际上,地震预警及紧急处置过程中数据打包、P波识别、信息排队等均存在一定的固定时延成分。因此,地震预警及紧急处置时延可以分为随机时延和偏置时延2部分。
随机时延的随机性强,而偏置时延相当于接近常量的偏移量。偏置时延无法避免,也就是说,地震预警及紧急处置时延不会小于1个最小值,在这一最小值时间内产出预警信息的可能性不存在。因而,用常规的正态分布、对数正态分布或伽马分布等描述地震预警及紧急处置时延均存在小概率情况下无法正确评价其特征的问题。
鉴于以上阐述的问题,为了更精确地描述地震预警及紧急处置时延特征,本文提出1种时延精确概率分布——偏置伽马分布,其概率密度函数为
T=f(t|α,β)
(1)
即T服从偏置伽马分布,记为
T~Γo(α,β,C)或T-C~Γ(α,β)t>C
(2)
其中,

(3)
式中:T为时延随机变量;t为时延随机变量取值;α为形状参数;β为尺度参数;Γo为偏置伽马函数;C≥0为偏置量,当样本数量足够大时,可以用样本最小值作为C的估计值。
偏置伽马分布的数学期望和方差分别为
E(T-C)=αβ
(4)
D(T-C)=αβ2
(5)
特征函数为
ψ(t-C)=[1-iβ(t-C)]-α
(6)
1.2 偏置伽马分布的可加性
偏置伽马分布是一种非对称、连续性分布。当偏置量C=0时,偏置伽马分布即为伽马分布。偏置伽马分布具有伽马分布的所有性质[10]。
1)尺度参数相同时的偏置伽马随机变量之和的分布
若T1~Γo(α1,β,C1)t1>C1,T2~Γo(α2,β,C2)t2>C2, 且T1与T2相互独立,则
T=T1+T2~Γo(α1+α2,β,C1+C2)
(7)
2)尺度参数不同时的偏置伽马随机变量之和的分布
若T1,T2, …,Tn为相互独立的偏置伽马随机变量,Ti~Γo(αi,βi,Ci)ti>Ci, 且偏置伽马随机变量之和T=T1+…+Tn,则
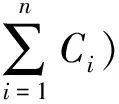
ti>Ci, 且Ci≥0
(8)
或
ti>Ci, 且Ci≥0
(9)
1.3 模型参数估计
1)偏置伽马分布的参数估计

(10)
(11)

2)偏置伽马随机变量之和分布的参数估计
采用矩匹配法可以得到偏置伽马随机变量之和分布的参数估计的近似解。利用矩匹配法,设Tm~Γ(αm,βm),则式(8)和式(9)中形状参数α*和尺度参数β*的近似解的取值范围为
(12)
(13)
式中:αmin为式(8)和式(9)中各个独立随机变量的形状参数α1,…,αn中的最小值;βmin和βmax为式(8)和式(9)中各个独立随机变量的尺度参数β1,β2,…,βn中的最小值、最大值。
采用Shai Covo法[12]也可得到偏置伽马随机变量之和分布的参数估计的近似解。则式(8)和式(9)中形状参数α*和尺度参数β*的近似解的取值范围为

(14)
(15)
其中,
(16)
1.4 地震预警与紧急处置策略
1.4.1 紧急处置路径
结合我国高速铁路技术体系,为保证地震紧急处置的可靠实施,设有3条紧急处置路径,如图1所示。

图1 高速铁路地震预警及紧急处置路径
紧急处置路径1(Ppath1):通过车载装置自动触发列车紧急制动。即由地震预警监测系统GPRS接口服务器(EM-GRIS)向铁路移动通信系统(GSM-R)发送信息;车载装置基于GPRS方式实现紧急处置信息的接收与应答;当接收到紧急处置信息后,车载装置自动触发动车组制动系统实施紧急制动,或由车载装置语音提示司机手动施加最大常用制动,使列车限速运行。
紧急处置路径2(Ppath2):通过触发列控系统自动控制列车紧急制动。即由地震预警监测系统向列控系统继电接口发送信息;列控系统侧当接收到地震紧急处置信息时,向地震防护区域内所有轨道区段发H码,列控中心向车站计算机联锁传送轨道区段全部占用信息;RBC根据轨道区段占用信息向相关列车发送CEM,UEM或SMA消息;同时,由列控中心向车站联锁传送区间占用信息,联锁关闭发车条件。
紧急处置路径3(Ppath3):通过触发牵引供电系统自动控制接触网断电。即由地震预警监测系统向牵引供电系统继电接口发送信息;牵引变电所2路高压断路器回路同时接收3组触发信号;第1组接点闭合以直接驱动高压断路器分闸,第2组接点闭合以通过综自装置驱动高压断路器分闸,第3组接点打开以通过综自装置报警。
3个紧急处置路径事件相互独立,则高速铁路地震紧急处置事件可定义为
EH⊆{Ppath1,Ppath2,Ppath3}
(17)
1.4.2 地震预警及紧急处置级别
根据地震警报级别,紧急处置由低到高划分为Ⅰ级、Ⅱ级和Ⅲ级处置。
Ⅰ级预警及紧急处置——地震加速度峰值大于等于40 gal且小于80 gal;采用路径1进行紧急处置。
Ⅱ级预警及紧急处置——地震加速度峰值大于等于80 gal且小于120 gal;采用路径1+路径2进行紧急处置。
Ⅲ级预警及紧急处置——地震加速度峰值大于等于120 gal;采用路径1+路径2+路径3进行紧急处置。
1.5 时延数学模型
依据高速铁路地震预警与紧急处置策略,地震预警及紧急处置综合时延可表示为
(18)
式中:TⅠ,TⅡ,TⅢ分别为Ⅰ级、Ⅱ级、Ⅲ级预警及紧急处置时延;PGACⅠ,PGACⅡ,PGACⅢ分别为Ⅰ级、Ⅱ级、Ⅲ级地震预警及紧急处置阈值,各自取值为40,80,120 gal。
1)Ⅰ级预警及紧急处置时延
Ⅰ级预警及紧急处置时延包括地震预警时延和Ⅰ级紧急处置时延,即

(19)
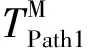
2)Ⅱ级预警及紧急处置时延
Ⅱ级预警及紧急处置时延包括地震预警时延和Ⅱ级紧急处置时延。在CTCS-3级列控系统模式下:

(20)


在CTCS-2级列控系统模式下:

(21)

3)Ⅲ级预警及紧急处置时延
Ⅲ级预警及紧急处置时延包括地震预警时延和Ⅲ级紧急处置时延。在CTCS-3级列控系统模式下:

TManual)]
(22)
式中:TPath3为通过触发牵引供电系统自动控制接触网断电的紧急处置时延。
在CTCS-2级列控系统模式下:

TManual)]
(23)
2 模型验证
利用某高速铁路地震预警及紧急处置系统试验实测数据,对地震预警及紧急处置不同时段的时延服从本文提出的偏置伽马分布的假设进行验证。试验方法是:将天然地震波记录数据按照各采集数据台站的实际时差进行回放,以此作为现场监测设备的输入,台站坐标按照各采集数据台站的实际经纬度进行设置,试验前用GPS时间校准。地震波选取震中距为50 km内、50~100 km和100 km以上的包括网内、网外及组合模式的国内和日本天然地震记录数据。除传感器外系统均为新研发的地震预警监测系统及车载地震紧急处置装置。
将地震预警及紧急处置在不同时段的时延数据进行统计分析,分别采用直方图、正态分布、对数正态分布、伽玛分布以及本文提出的偏置伽玛分布,对各时延的分布参数进行极大似然估计,得出其概率分布密度函数。其中单台地震预警时延(首台站P波初至到地震预警监测铁路局中心系统发出地震预警信息首报的时延)概率密度函数拟合曲线(样本数300,实测最小值0.924 s,最大值4.719 s)如图2所示;通过通信系统由车载装置自动控车时延的概率密度函数拟合曲线(样本数720,实测最小值0.295 s,最大值4.769 s)如图3所示;基于CTCS-2通过触发列控系统自动控车时延的概率密度函数拟合曲线(样本数181,实测最小值2.946 s,最大值6.670 s)如图4所示;通过触发牵引供电系统断电时延的概率密度函数拟合(样本数65,实测最小值0.165 s,最大值0.668 s)如图5所示。

图2 单台地震预警时延的概率密度函数拟合

图3 通过通信系统由车载装置自动控车时延的概率密度函数拟合
对于地震预警与紧急处置而言,无时延的系统尚不存在,学者们更为关注的是最小时延,即系统实时性问题[11]。由图2—图5看出:4种时延用正态分布、对数正态分布或伽马分布函数进行拟合时,在时延为0 s或附近时仍为小概率事件,这与实际不符;而偏置伽马分布概率密度函数可有效地描述时延的偏置量(最小时延)、非正态形态以及分布特征,能正确描述地震预警与紧急处置系统的实时性。
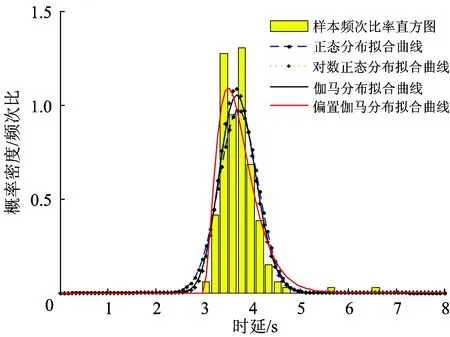
图4 基于CTCS-2通过触发列控系统自动控车时延的概率密度函数拟合

图5 通过触发牵引供电系统断电时延的概率密度函数拟合


表1 地震预警及紧急处置时延分布参数估计
3 地震预警及紧急处置时延综合分析
地震预警及紧急处置总时延涉及高速列车紧急制动试验,受实车试验条件、试验成本等限制,无法获取大样本时延数据,本文利用上述试验数据并采用所提出的偏置伽马分布模型和概率事件分析模型方法分析高速铁路各级别地震预警与紧急处置总时延分布特征与规律。
3.1 Ⅰ级预警及紧急处置总时延
Ⅰ级预警及紧急处置总时延为地震预警时延、基于GPRS方式向车载装置发送地震紧急处置信息时延与司机反映时延之和。由于各时延是相互完全独立的事件,所以遵循偏置伽马分布的可加性,则Ⅰ级预警及紧急处置总时延变量式(19)服从本文提出的偏置伽马分布,记为
TⅠ=TEEW+TGPRS+TManual~Γo(α,β,C)
(24)

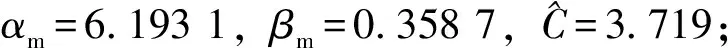

图6 Ⅰ级预警及紧急处置总时延概率密度曲线
3.2 Ⅱ级预警及紧急处置总时延
Ⅱ级紧急处置在车载装置触发列车紧急制动和列控系统行车控制2种路径下共同作用,且2种路径事件相互独立。因此Ⅱ级预警及紧急处置在CTCS-3级列控系统模式下总时延变量式(20)可以改写为

(25)
其遵循偏置伽马分布的可加性,即
(26)
(27)


图7 Ⅱ级预警及紧急处置路径1总时延概率密度曲线

图8 Ⅱ级预警及紧急处置路径2且CTCS-3模式条件下总时延概率密度曲线

同理,Ⅱ级预警及紧急处置在CTCS-2级列控系统模式下总时延变量式(21)可以改写为
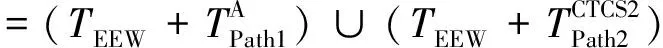
(28)
其遵循偏置伽马分布的可加性,即
(29)


图9 Ⅱ级预警及紧急处置路径2且CTCS-2模式条件下总时延概率密度曲线
3.3 Ⅲ级预警及紧急处置总时延
Ⅲ级紧急处置在车载装置触发列车紧急制动、列控系统行车控制和接触网断电后司机自然反应用手动控车3种路径下共同作用。由于接触网断电后司机自然反应用手动控车与管理规定及司机地震安全意识等诸多因素有关,所以前2种路径事件远远早于路径3而发生。
(30)
除非在前2种路径均发生故障情况下,路径3事件才有可能独立发生,因此路径3事件独立发生概率很低,可忽略不计。简化后,可认为Ⅲ级预警及紧急处置总时延与Ⅱ级预警及紧急处置总时延相同,其结果本文不再重述。
3.4 综合比较
分别将Ⅰ级预警及紧急处置,Ⅱ和Ⅲ级预警及紧急处置路径1,Ⅱ和Ⅲ级预警及紧急处置路径2且CTCS-3模式,Ⅱ和Ⅲ级预警及紧急处置路径2且 CTCS-2模式的总时延的累积概率分布曲线如图10所示,其在50%,70%及95%概率情况下的总时延见表2。

图10 不同紧急处置级别不同路径的总时延累积概率分布比较

表2 不同累积概率时的地震预警及紧急处置总时延比较
由图10及表2可以看出:Ⅱ,Ⅲ级预警及紧急处置路径1 ,即基于GPRS方式传输紧急处置信息并由车载装置自动控车的总时延最小,实时性最好;其次分别为Ⅱ,Ⅲ级预警及紧急处置路径2且 CTCS-2模式,Ⅰ级预警及紧急处置,Ⅱ,Ⅲ级预警及紧急处置路径2 且CTCS-3模式。由于Ⅰ级地震预警对高速列车运行安全性影响相对较小,故Ⅰ级预警及紧急处置的实时性要求可相对放宽。Ⅱ级和Ⅲ级预警及紧急处置时车载装置与列控系统均自动控车,可起到互补作用,更有利于保障安全。
4 结束语
高速铁路地震预警及紧急处置的关键问题是系统实时性,解决这个科学问题是实现系统工程化的关键环节。通过采用本文提出的偏置伽马分布模型对某高速铁路地震预警系统试验时延测试数据进行分析,证明该模型可以准确、有效地描述地震预警及紧急处置时延的分布特征,可对地震预警及紧急处置时延进行预测与评价。采用本文提出的不同紧急处置路径和不同预警与紧急处置级别情况下时延的概率事件模型,可有效地预测与评价高速铁路各级别地震预警与紧急处置在不同路径条件下总时延特性。经综合分析比较,进一步证明我国高速铁路地震预警及紧急处置技术方案有效、可行。
