基于载荷加载次序的疲劳寿命预测改进模型
2019-02-19薛齐文杜秀云王生武
薛齐文,杜秀云,王生武
(1.大连交通大学 土木工程学院,辽宁 大连 116028;2.辽宁师范大学 物理与电子技术学院,辽宁 大连 116029)
随着我国铁路货运重载和客运高速的跨越式发展,焊接承载部件现已大量地存在于各类新型机车车辆结构中,而疲劳开裂破坏是这些焊接承载部件主要破坏方式之一。由于疲劳寿命预测关系着整个焊接结构的安全问题,在国内铁道车辆行业目前急需更为合理的疲劳寿命预测技术,以满足工程实际的迫切需要。开展焊接承载结构的寿命预测研究具有十分重要的工程实用意义[1-2],众多的专家学者也针对该问题开展了大量的研究工作,并取得了不少成果[3-5]。
对于实际中复杂机车车辆结构的一些关键焊接部件,如列车转向架构架焊接接头等,其承载状态的一个显著特点是承受多级小载荷作用。在进行疲劳损伤评估时,小载荷的作用不可忽视,必须加以考虑,否则预测结果将过于保守,不利于焊接结构的安全使用。对于小载荷对疲劳损伤的影响,Corten-Dolan模型能很好地进行描述,且还能处理载荷间的作用效应。虽然利用该模型进行疲劳累积损伤的评估和寿命预测,在实际工程中得到了一些应用[6-9],但是该模型中关键参数d直接关系着疲劳寿命的预测精度,其确定存在争议[10]。因此,Corten-Dolan模型中参数d如何确定是研究的重点,有必要开展进一步分析及探讨。
最早参数d被认为保持不变,可通过2级载荷疲劳试验进行确定[11]。随后研究发现,参数d不能看作固定不变的常数,虽可通过疲劳试验确定该参数,但不同的疲劳载荷试验得到的数值差异很大[12]。文献[13]考虑了应力状态、实时损伤对疲劳累积损伤的影响,重新定义了参数d的函数,数值验证也取得了较好的效果,明显提升了模型的预测精度,但预测精度仍有待进一步提高。
在实际的机车车辆服役环境中,车辆结构的焊接部件受力状态非常复杂。对于复杂多级载荷作用下的疲劳累积损伤,还应充分考虑载荷加载次序和载荷间的相互影响。Corten-Dolan模型及既有的改进模型中关键参数d虽能体现载荷间的相互作用,但未能考虑载荷加载次序对疲劳损伤累积的影响,将在很大程度上影响预测结果,且预测结果具有较大的分散性,往往难以满足实际工程需求。
本文在考虑小载荷、损伤程度和应力状态的基础上,进一步考虑载荷加载的次序关系,对Corten-Dolan模型进行改进,并采用常用材料、合金材料以及Q235B钢焊接接头的试验数据进行有效性和可行性验证。
1 Corten-Dolan模型及既有的改进模型
根据Corten-Dolan模型,常幅载荷作用下,在经历n次应力循环后,疲劳累积损伤Dd可为
Dd=prna′
(1)
式中:p为应力作用下的损伤核个数;r为损伤系数;a′为与材料相关的常数。
由式(1)可知,临界疲劳损伤Dc为
(2)
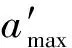
变幅载荷作用下,可按照总损伤量建立疲劳累积损伤等式,即各段损伤的总和应等于常幅载荷单独作用下的损伤之和。在多级变幅载荷作用下直至破坏所对应的累积损伤Dd与临界疲劳损伤Dc一致,则有
(3)
式中:i为应力循环的级数。
进行疲劳失效分析时,在多级载荷作用下,经历多级应力循环作用下的Corten-Dolan模型疲劳寿命预测公式可表示为
(4)
式中:Nf为多级应力循环作用下模型所预测的疲劳寿命;ai为第i级应力循环数占总循环次数的百分比;σi第i级应力;σmax为多级应力中的最大应力。
式(4)中,参数d与材料属性、应力水平相关,文献[13]将参数d定义为1个包含循环次数比和应力比的函数,为
(5)
式中:ni为实际应力循环对应的疲劳寿命;Nfi为第i级应力σi单独循环作用下的疲劳寿命。
式(5)中引入了1个参数γ,该参数为与材料相关的常数,可根据试验数据结合疲劳失效判据进行拟合确定。将式(5)代入式(4)则Corten-Dolan模型的既有改进模型可表示为
(6)
根据式(5)定义的参数d,对应的Corten-Dolan模型的既有改进模型还可以写成另一种表达形式,为
(7)
相比较于Miner法则和Manson-Halford模型而言,Corten-Dolan模型的既有改进模型以各级应力与最大应力的比值体现载荷间的相互作用并考虑了小载荷的贡献,使疲劳寿命预测结果具有较高的可信度,但唯一的参数d的计算尚待进一步讨论。
2 基于载荷加载次序的Corten-Dolan改进模型
Corten-Dolan模型的既有改进模型中未考虑实时的各级载荷加载次序情况的影响,且是基于线性Miner累积损伤理论推导出来的,而Miner累积损伤是与载荷加载先后次序无关的。但是,众多的试验数据表明,疲劳累积损伤是与载荷加载次序相关的。对于简单的2级试验加载,破坏时的疲劳累积损伤往往不等于1,当采用先低后高的载荷加载次序时,其疲劳累积损伤∑ni/Nfi>1,使裂纹萌生时间推迟;当采用先高后低的载荷加载次序时,其疲劳累积损伤∑ni/Nfi<1,高应力使裂纹提前形成,低应力使裂纹扩展。对于多级载荷加载,可以得到相同的结论。
根据上述分析,对关键参数d进行修正定义时,除考虑小载荷、实时损伤、应力状态对疲劳累积损伤的影响外,还需进一步考虑载荷加载次序的影响,从而实现对Corten-Dolan模型既有改进模型的进一步改进。
考虑到实际工程中,往往是多级变幅载荷作用,不宜考虑加载前所有级别的载荷,因此只考虑相邻2级载荷加载先后次序影响,对参数d进行修正,可以有下述2种修正方法。
方法1:直接在式(5)的基础上增加应力比系数对d进行修正,则有
(8)

将式(8)代入式(6),可以得到采用方法1修正后得到的改进疲劳寿命预测模型1(简称预测模型1)为
(9)
方法2:因参数γ为与材料相关的常数,它对关键参数d的贡献度是固定不变的,且将载荷加载次序影响以及损伤程度的影响分别作为独立的影响因素对d进行修正,则有
(10)
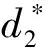
将式(10)代入式(6),可以得到采用方法2修正后所得的改进疲劳寿命预测模型2(简称预测模型2)为
Nf=
(11)
采用上述2种模型对关键参数d修正后,当相邻载荷σi+1/σi>1即采用先低后高的载荷加载次序时,得到的预测寿命有所增加;当相邻载荷σi+1/σi<1即采用先高后低的载荷加载次序时,得到的预测寿命有所减少,这同疲劳累积损伤与载荷加载次序关系的分析一致。
式(11)中的未确定参数γ,可以利用试验测量数据,借助反演优化的手段,采用2种预测模型对其进行反演识别。在反演识别参数γ时,由试验测量数据和2种预测模型分析结果,根据最小二乘原理构建目标函数,采用一维搜索方法可较为容易地识别出来。
3 数值算例
为验证基于载荷加载次序的Corten-Dolan改进模型疲劳预测能力,采用文献[13]所给的标准45号钢、标准16Mn钢、热轧16Mn钢等试验数据进行疲劳寿命预测。通过模型预测值与试验数据的对比,对改进模型的预测准确性进行了验证,并将不同模型的预测结果进行对比。
算例1:2级载荷作用下焊接材料的疲劳寿命预测
标准45号钢的2级载荷分别为331.46和284.40 MPa,它们单独作用下焊接接头的疲劳寿命分别为5.0×104和5.0×105次,各种加载模式(不同的载荷加载次序对应的应力水平以及不同应力循环次数)下采用不同方法得到的参数d计算结果及不同模型下的疲劳寿命预测结果对比情况分别见表1和表2。

表1 标准45号钢在不同加载模式、不同求解方法下的参数d计算结果对比

表2 标准45号钢在2级载荷作用下采用不同模型预测得到的疲劳寿命
对于标准16Mn钢,2级载荷分别为562.9和392.3 MPa,它们单独作用下焊接接头的疲劳寿命分别为3.968×103和7.8723×104次,各种加载模式下采用不同方法得到的参数d计算结果及不同模型下的疲劳寿命预测结果对比情况分别见表3和表4。
对于热轧16Mn钢,2级载荷分别为394和345 MPa,它们单独作用下焊接接头的疲劳寿命分别为9.35×104和4.022×105次,各种加载模式下采用不同方法得到的参数d计算结果及不同模型下的疲劳寿命预测结果对比情况分别见表5和表6。
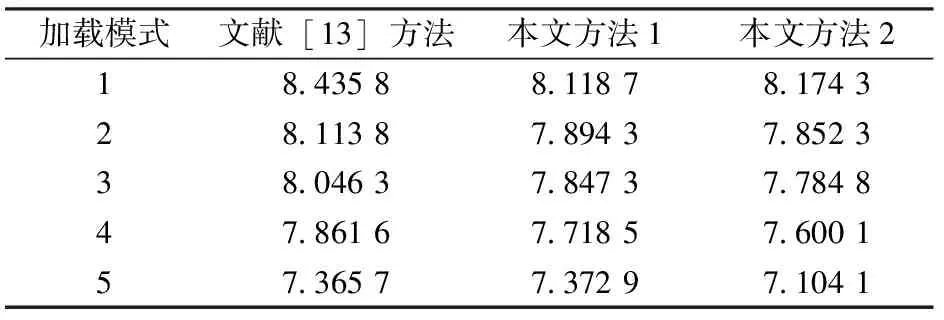
表3 标准16Mn钢在不同加载模式、不同求解方法下的参数d计算结果对比
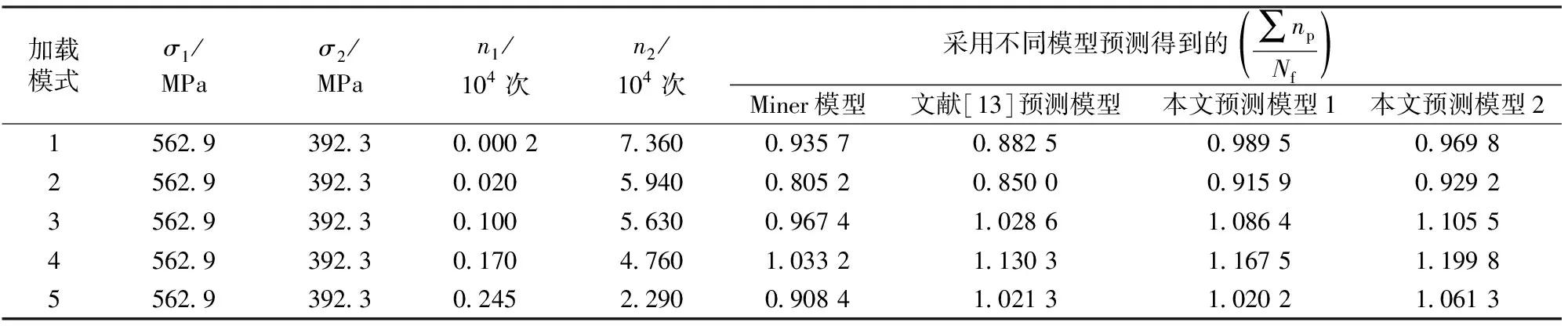
表4 标准16Mn钢在2级载荷作用下采用不同模型预测得到的疲劳寿命

表5 热轧16Mn钢在不同加载模式、不同求解方法下的参数d计算结果对比
由上述计算结果可知,在2级载荷作用下,对于标准45号钢、标准16Mn钢以及热轧16Mn这3种材料,采用本文基于载荷加载次序的Corten-Dolan改进模型均能够对焊接接头的疲劳寿命进行较为准确的预测。相对于线性Miner法则以及文献[13]中的改进方法,本文2种预测模型的预测结果均有较为明显的提高。
算例2:多级载荷下焊接接头的疲劳寿命预测
利用文献[13]中对Q235B钢变幅加载条件下的试验数据,以5级载荷为例,采用不同预测模型对其焊接接头进行疲劳寿命预测,预测对比结果见表7。
由表7的计算结果可知,对Q235B焊接接头,在5级变幅载荷作用下,采用所改进的Corten-Dolan模型也能对其疲劳寿命进行预测,相对于传统的Miner法则以及文献中模型,预测精度也有明显的提高。
4 结 论
(1)建立了基于载荷加载次序的Corten-Dolan改进模型,充分地考虑了小载荷、损伤程度、应力状态以及载荷加载次序的影响,可有效地进行疲劳寿命预测。

表6 热轧16Mn钢在2级载荷作用下采用不同模型预测得到的疲劳寿命
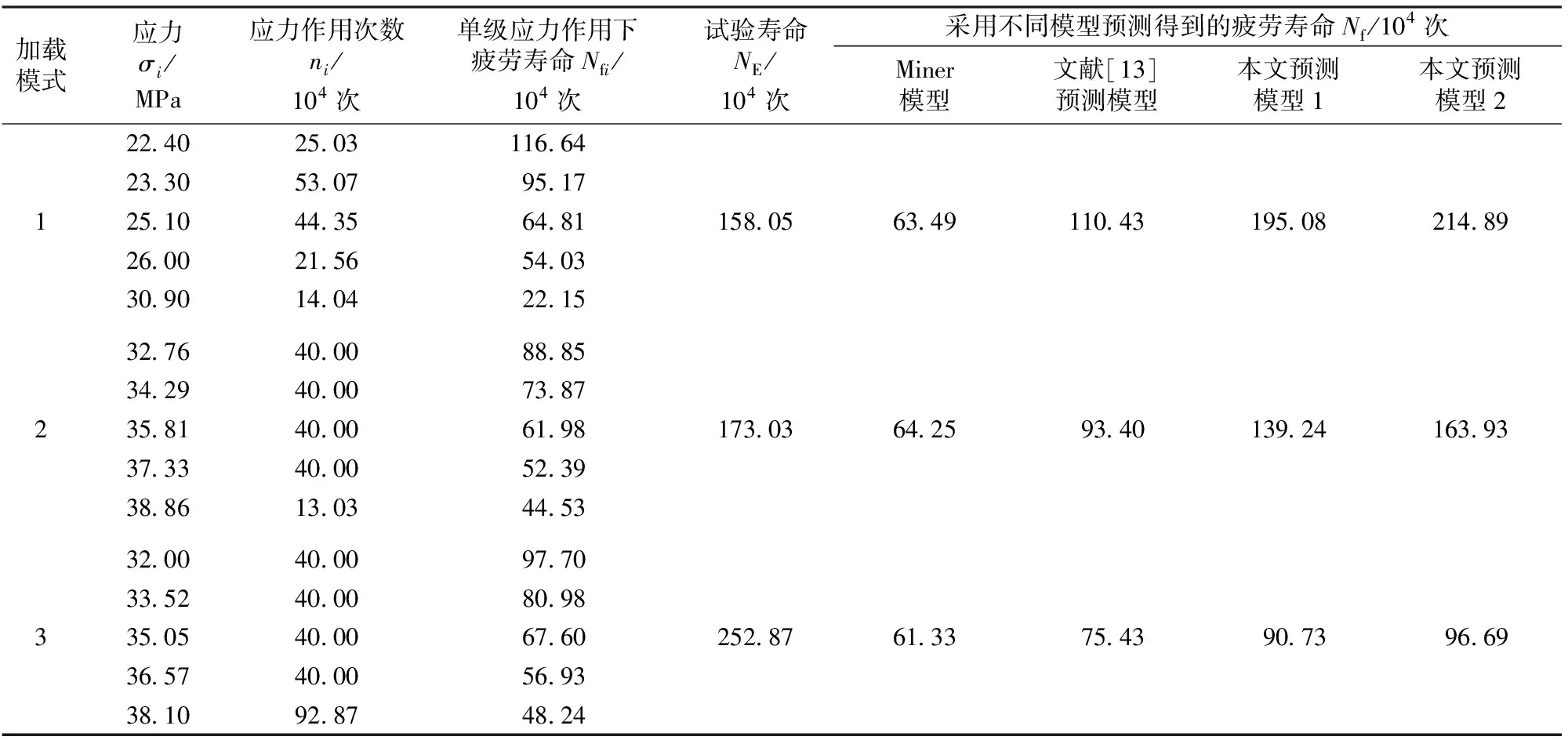
表7 Q235B焊接接头在多级载荷作用下采用不同模型预测得到的疲劳寿命
(2)根据常用材料、合金材料以及Q235B钢的焊接接头试验数据验证结果,与传统的Miner模型相比,无论是在2级载荷作用下,还是在多级载荷使用下,本文的2种改进模型都具有很好的可行性,同时预测精度得到明显的提升,预测结果更加可靠。
(3)本文改进模型的形式相对较为简单,不需要多层迭代计算,很少的模型参数也容易确定,便于应用于工程焊接结构的疲劳寿命预测。
