一种基于离散模块的浮体水弹性响应预报方法
2019-02-16付世晓宋春辉
位 巍 , 付世晓 , 宋春辉
(1.上海交通大学 海洋工程国家重点实验室,上海 200240;2.高新船舶与深海开发装备协同创新中心,上海 200240)
0 引 言
近三十年来,超大型浮体在海上资源开发、海洋空间利用以及海上军事基地建设等方面发挥了重大的作用。最早进行超大型浮体研究的是日本和美国,日本在90年代提出了箱式超大型浮体,主要用于海上机场、离岸集装箱码头等作用[1];美国为了满足其军事需求,建造了移动式海上基地[2];挪威正在发展水下浮桥,用于连接和跨越该国的多个海湾[3];我国在岛礁附近布置超大型浮体作为物流基地和保障[4-5]。与常规的海洋浮式结构物或海洋船舶相比,超大型浮体由于其尺寸巨大,相对刚度较低,因此在其动力响应和结构分析时必须采用水弹性的方法。
目前,对于其响应和受力的分析主要基于水弹性理论[6-8]。吴有生和杜双兴[9]采用三维线性水弹性理论对弹性连接的多刚体系统的模型的结构运动和连接件的应力响应进行了分析,为此类结构连接器的设计提供参考。Fu和Moan[10]采用三维水弹性方法求解了带有复杂连接的结构的水弹性响应,并对连接件的位移响应进行了研究。宋晧和崔维成[11]采用多重尺度法和常规的有限水深格林函数法对置于非均匀海底上的超大型浮体的响应进行了分析,并与试验结果进行了对比,证明非均匀海底对超大型浮体有一定影响。虽然基于模态叠加的水弹性方法已经经过了长足的发展并且已被广泛地应用于超大型浮体的水弹性响应的计算中[8,12],但是对于工程中关心的连接器的受力,该方法研究较少;另一方面,超大型浮体面临的非均匀海洋环境问题并没有得到很好的解决。
本文基于多体动力学和有限元方法,建立了一种求解浮体水弹性响应的数值方法[13-14]。此方法中,将连续的浮体离散为若干个刚体子模块,基于三维势流理论并考虑各模块之间的水动力干扰,求得作用在各模块上的波浪激励力以及附加质量和阻尼系数;各模块之间通过等效梁的刚度阵连接,从而保证浮体变形的连续性;将各模块的水动力系数以及波浪激励力和子模块之间的刚度阵耦合,从而建立了多模块系统的运动方程。进一步,通过模态叠加方法,将本文提出的数值计算方法与传统的水弹性方法建立联系。本文的方法不仅可以求解位移响应和结构内力,也可以求得主坐标响应和广义波浪激励力,而后两者原先只能通过传统的水弹性方法得到。通过两种方法的对比,验证了本文的数值方法在求解水弹性响应中的正确性。本文的方法基于多模块的思想,有利于对非均匀海洋环境和连接件的受力进行分析。
1 理论背景
1.1 坐标系的定义
为了描述N个浮体组成的多浮体系统在波浪作用下的运动响应,采用三套右手坐标系,分别为大地坐标系OXYZ、随体坐标系omxmymzm以及参考坐标规定波浪入射角方向与X轴平行且指向X轴正向时,θ=0°,逆时针方向为正。

图1 多体系统的坐标系定义Fig.1 Coordinate system of multiple floating body system
1.2 波浪激励力以及附加质量和阻尼系数
基于多体动力学理论和线性化的伯努利方程,可以得到作用在各浮体上的波浪激励力,附加质量和阻尼系数:

其中:S()m为浮体m静置于静水中时的湿表面积;μ和c分别表示附加质量和阻尼系数,当m=n时,表示由于浮体m本身的运动引起的附加质量和阻尼系数;m≠n时表示由于浮体n的运动引起的浮体m的附加质量和阻尼系数。
1.3 频域内运动方程
对于连续的超大型浮体,将其离散为有限个刚体模块后,单独的刚体模块不仅受相邻模块的水动力干扰,而且还受到相邻模块运动位移的限制,即必须要保证整个浮体的变形是连续的。相邻的模块之间通过在其等效中心设置伯努利——欧拉梁进行连接。因此,基于多体动力学以及有限元的思想,可以建立浮体在波浪作用下的浮体的动力学方程:

其中:[M],[A],[C]分别为各子模块组成的质量矩阵、附加质量矩阵以及阻尼矩阵;[c]为结构的阻尼矩阵;[K]为子模块静水恢复力矩阵;[k]为模块之间连接处的总刚度阵;{x}为各模块的位移值;{Fw}为各子模块受到的波浪激励力。

1.4 与传统水弹性方程的关系
方程(3)也可以看作是有N个节点的结构的有限元方程,每个节点有六个自由度。解此运动方程一般有两种方法,一类是直接积分法,就是按时间历程对上述微分方程直接进行数值积分,常用的方法有Newmark法、Wilson-θ法;另一类是模态叠加法(Mode Superposition Method),这里介绍模态叠加法。
对于连续结构的系统,在外力的作用下通常只被激起较低一部分的振型,而大部分高阶振型被激起的分量很小,一般可忽略不计,因此假若对运动方程(3)起主要作用的是其前m阶振型,则浮体的位移响应可以由m阶振型线性叠加得到,可以表示为

其中:pr(t)为系统的第r阶主坐标响应,{p}为主坐标响应列阵,为m×1的列阵;{Dr}为第r阶振型向量,[D]为振型矩阵,[D]= [{D1},{D2},…,{Dm}],为 6N×m的矩阵;当r=1,…,6 时,{Dr}表示结构的前6阶刚体运动模态列向量,可以写为:
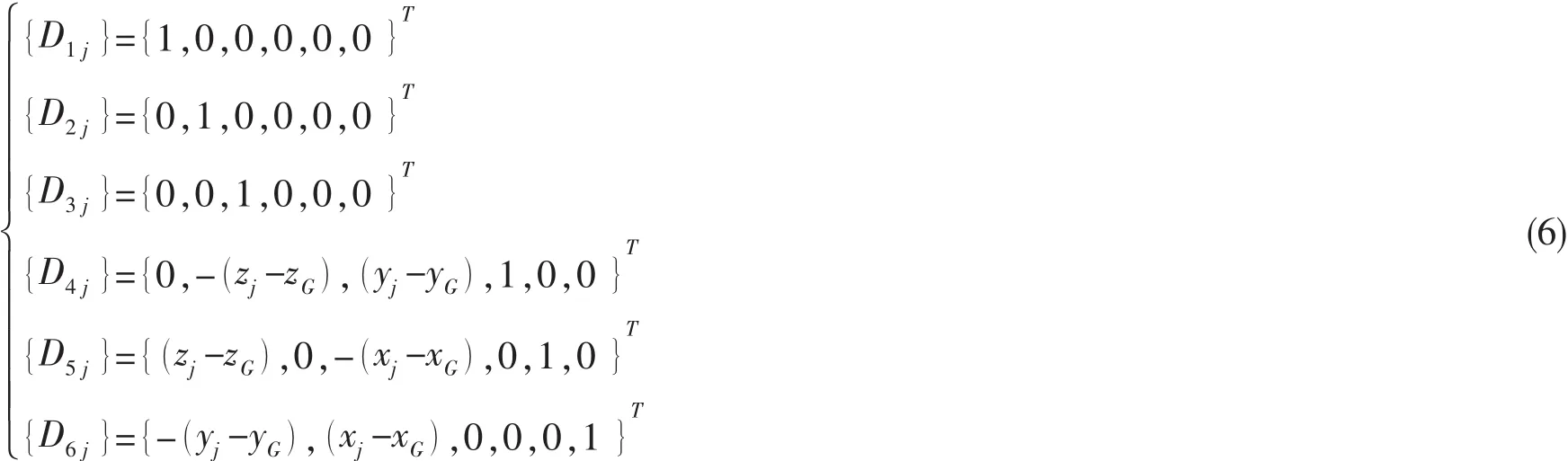
其中: (xG,yG,zG)为连续浮体的重心的位置, (xj,yj,zj)为连续浮体上第j个节点在随体坐标系中的坐标值。
将(5)式代入到方程(3)中,得

将上述方程左右两边同时乘以[D]T,得到

由振型关于质量阵和刚度阵的正交性可知,

其中:[m],[b],]分别为浮体的广义质量阵、广义阻尼和广义刚度阵;[a],[B],]分别为流体的广义附加质量、广义阻尼和广义流体恢复力系数矩阵;}为广义波浪激励力列阵,这些参数的表达式为:

上式即为广义线性水弹性运动方程式,本文的数值计算方法最后可以回归到传统的水弹性方程中。
方程(9)中的各个变量,既与空间坐标有关又与时间变化有关,对于以稳定频率作周期变化的变量可以写为:,以便于分离空间和时间。 将方程(9)中的时间变量从其方程中分离出去,方程(9)的频域表达式为:

其中:{u}为连续浮体的主坐标响应。
上式即为连续浮体的三维水弹性时域方程,根据上述推导,可以根据本文的数值计算方法求解作用在连续浮体上的广义波浪激励力、广义附加质量、广义阻尼以及主坐标响应。
2 数值计算结果
2.1 模型介绍
为了验证本文数值计算方法的正确性,选取Fu论文中的超大型浮体作为本文的数值计算模型,并将其吃水改为5 m,其参数见表1。

表1 超大型浮体的主尺度Tab.1 Main particulars of VLFS and substructures
2.2 垂向位移、弯矩、剪力和扭矩验证
由于本文的数值模型采用了新的吃水和新的弯曲刚度,为了验证其可靠性和与传统的三维水弹性的关系,首先对此模型在频域内的垂向位移和弯矩与三维水弹性程序的结果进行对比验证,并在此基础上进一步给出浮体在各个弹性模态下的主坐标响应以及广义力。本文仍将整个模型离散为8个模块,对其垂向位移、垂向弯矩以及剪力进行求解,如图2所示。

图2 模型的水动力网格的俯视图以及等效梁模型Fig.2 Schematic plane view of grid model of VLFS and equivalent beam model
图3给出了在45°浪向角时采用本文的数值计算方法和三维水弹性方法得到的垂向位移、弯矩、剪力和扭矩的对比结果图,可以看出两种数值方法的结果吻合良好,证明本文在频域内建立的数值方法对于此模型有同样的适用性。

图3 浮体的垂向位移、垂向弯矩、剪力以及扭矩在45°浪向下的两种数值方法的对比Fig.3 Comparison of the vertical displacement,vertical bending moment,vertical shear force and torsional moment between the 3D hydroelasticity and the present method in wave heading of 45°
2.3 主坐标响应验证
基于本文的数值方法得到的上述的水弹性的结果,垂向位移、弯矩等参数都是与划分的模块个数相等的离散点,为了得到浮体的变形的连续结果,可以根据第二章提到的逆模态叠加的方法,根据已知点上的垂向位移、扭转角等信息求取浮体各模态上的主坐标响应。在模态叠加法中,根据浮体的垂荡、纵摇以及各阶垂向弯曲模态的主坐标响应求取浮体的垂向位移。因此,在已知8点的垂向位移时,可以求得浮体的垂荡响应、纵摇响应以及前6阶垂向弯曲模态的主坐标响应幅值。

图4 两种数值方法下浮体的垂荡响应幅值、纵摇响应幅值以及第7、8阶主坐标响应幅值的对比Fig.4 Comparison of the heave,pitch RAO and the principal coordinate of the vertical bending modes between the 3D hydroelasticity and the present method

图5 两种数值方法下浮体的横摇响应幅值以及第11阶主坐标响应幅值(扭转模态)的对比Fig.5 Comparison of the roll RAO and the principle coordinate of the torsional modes between the 3D hydroelasticity and the present method
图4给出了反推得到的结构的垂荡、纵摇以及前两阶垂向弯曲模态的主坐标响应随入射波浪频率的变化趋势,并与三维水弹性的结果进行对比。从图中可以看出,本文得到的结果与三维水弹性的结果吻合良好,证明了本文的方法在求解结构的水弹性主坐标响应的正确性。进一步,根据得到的浮体的主坐标响应,可以采用模态叠加的方法,得到结构连续的垂向位移、垂向弯矩和剪力。
与垂向位移的求解相似,对结构模态分析后,得到浮体的扭转模态。同样根据离散点上的扭转角,利用逆模态叠加的思想,可以得到浮体的横摇角以及各扭转模态下的主坐标响应。图5给出了使用本文的方法计算得到的横摇RAO以及第一阶扭转模态的主坐标响应与水弹性方法的对比结果。从图中可以看出,本文方法得到的扭转模态的主坐标响应与水弹性方法得到的结果吻合良好。根据得到的主坐标响应可以进一步通过模态叠加的方法,得到作用在浮体上的连续的扭矩。
2.4 波浪激励力验证
根据第二章的理论,各个子模块上的波浪激励力乘以振型的转置即为浮体受到的波浪激励力,将其与三维水弹性方法得到的广义波浪激励力进行对比,图6主要给出了与垂向弯矩和扭转相关的模态上的波浪激励力。从图中可以看出,本文数值计算方法得到的广义波浪激励力与三维水弹性的结果吻合较好,但在某些较高的频率下(波长较小时),在其位置不会出现峰值,这可能是因为划分的子模块个数的限制,不能体现高频特性。因此,如果要对浮体高频下的响应特性进行研究,可以将浮体划分更多的模块。

图6 两种数值方法下浮体的波浪激励力的对比Fig.6 Comparison of the wave exciting forces between the 3D hydroelasticity and the present method
3 结 论
本文基于传统的水动力学和有限元法,通过将连续的模型离散,提出了一种新的水弹性响应的分析方法。采用提出的方法对一超大型浮体的水弹性响应进行研究,将得到的垂向位移、弯矩、剪力、扭矩、主坐标响应以及波浪激励力与传统的水弹性得到的结果进行对比,吻合良好,证明了本文提出方法的正确性和可靠性。此外,本文的数值方法是基于离散模块的思想,可以为以后连接件受力分析以及非均匀海洋环境的分析提供依据。
