基于知识图谱的运筹学发展现状及趋势研究
2019-02-15陈江涛吕建秋
陈江涛, 吕建秋
(华南农业大学 数学与信息学院,广东 广州 510642)
0 引言
随着知识经济以及大数据时代的到来,数据的增长速度已经远远超出了人们的想象,人们越来越需要借助于一定的可视化技术来帮助分析和梳理相关知识领域研究现状,了解学科发展的新情况。借助科学知识图谱,人们可以透视庞大的知识体系中各个领域的结构,理顺当代知识大爆炸形成的复杂知识网络,预测科学技术知识前沿发展的最新态势[1]。Citespace软件是美国Drexel大学陈超美博士和大连理工大学WISE实验室联合开发的一款知识图谱可视化分析工具,现已被广泛运用于知识图谱的分析实践之中,本文主要借助于Citespace软件来分析近年来运筹学的发展现状及趋势。
1 数据的搜集和整理
Citespace软件可以直接用来分析web of science上导出的数据格式,进入web of science的核心合集数据库,选择SCI索引,输入主题词“Operations Research or Operational Research”,并选择2006年到2015年作为时间跨度,可以检索到3166篇文献,将其保存为可供Citespace分析的文献格式。
2 研究结果及分析
主要通过运用Citespace软件中的合作共现图谱梳理了近十年来运筹学研究的地域分布,通过对被引文献的关键节点分析了运筹学发展的基础知识,通过施引文献的聚类图谱分析了运筹学领域的研究前沿。
2.1 运筹学研究的主要国家和机构

图1 运筹学合作图谱
在Citespace软件中选择Country和Institution为图谱的网络节点,选择寻茎算法对图谱进行修剪和优化,可以得到如图一所示的研究机构分布图谱,其中圆形节点代表的是国家,分支节点代表的是机构。通过对图谱显示阈值的设定,可以显示出其中一些重要的研究机构。
从图1可以看出,近十年来运筹学研究区域分布呈现出五个明显的聚类,美国、英国、中国、加拿大和台湾。其中圆形节点的半径越大表示其发文频次越高。可以看到一些发达国家的运筹学发展研究依然走在世界前列,另外一些港口城市,如中国台湾、新西兰、中国香港在这方面的成果也比较多。

表1 运筹学发文情况统计表
由表1可以看出,从文献发表的频次来看,美国的发文数量要远高于其他国家,为1185篇。其次是英国、中国大陆、中国台湾和加拿大。从节点的中心性来看中国大陆和英国有着明显优势,这说明,在网络节点中,这两个节点与其他节点存在更多的合作关系。从中可以得出结论,近十年来美国依然在运筹学研究上处于绝对优势地位,研究成果远远高于其他国家。另外,作为运筹学发源地之一的英国,也是运筹学研究的主要国家之一,并且积极与其他国家的运筹学研究展开合作。另外,中国的运筹学研究近十年来也取得了较好的成果,发文频率排在第三位,中心性排在第一位,说明中国的运筹学研究越来越重视与其他国家的研究展开合作。
2.2 运筹学研究的重要文献
在Citespace软件中选择共引文献作为网络节点,阈值选用每年被引频次在前50的文献,采用寻茎算法作为网络图谱的修剪法则,运行Citespace软件,可以得到图2所示的图谱,其中节点表示被引文献,用年轮表示其被引年份,节点半径越大,表示文献的被引频率越高。

图2 运筹学引文共现图谱
从论文的被引频率来分析,可以看到对近十年来运筹学发展有较大影响的论文有,Stahlbock R在2008年发表的《Operations research at container terminals: a literature update》,该篇文章主要对运筹学在集装箱运输领域,如港口的作业组织和控制,码头运作计划和调度的数学解析法,仿真方法,智能优化方法等进行了系统地概括,文献回顾和趋势总结,推动了运筹学中排队论、图论、最优化方法、运输问题等在港口码头计划调度中的作用[2]。第二篇引用频率较高的是Charnes A于1978年发表的《Measuring the efficiency of decision making units》,该篇文章是由Charnes A,Cooper W W,Rhodes E合著的,并提出了著名的C2R模型,提出了一个对多投入,多产出效率决策单元的有效评价方法,从而开创了数据包络分析的方法[3]。第三篇重要文献是 Garey M R发表的《Computers and intractability: a guide to the theory of NP-completeness》,该篇文章搜集了从1978年夏天到1979年之间已经发现的三百个具有NP完全性的问题,从而成为计算机复杂算法研究人员不可缺少的一篇著作,其中对于图论,网络设计,存贮与检索,排序与优化,数学规划等问题被广泛应用于运筹学研究[4]。另外一篇较有影响的文章是Banker R D, Charnes A,Copper W W于1984年发表的《Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis》,在该文章将在C2R模型中规模收益不变的假定,改为规模收益变动的假定,提出BC2模型,与CCR模型共同构成DEA数据包络分析的基础模型[5]。还有一些关键节点如Goldberg D E在1989年发表的 《Genetic Algorithm in Search, Optimization, and Machine learning》 总结了遗传算法研究的主要成果,对遗传算法作了全面而系统的论述[6],一般认为,这个时期的遗传算法从古典时期发展了现代阶段,这本书则奠定了现代遗传算法的基础。另外还有Saaty T L在1980年出版的《The analytic hierarchy process: planning, priority setting, resources allocation》,重点介绍了AHP方法如何综合定性与定量分析,模拟人的决策思维过程,解决多因素复杂系统,特别是难以定量描述的社会系统的方法,对决策论的发展起了重要作用[7]。除了这些共引次数较高的节点外,还有一些其他节点也十分重要。
由于本文选取的是近十年来的施引文献,运筹学发展前期产生的一些重要基础性文献可能并未表现出较高的被引频率,在网络节点中表现的不是很明显,但我们依然可以从时间线图谱出找出一些时间较远却依然保持着一定被引频率的经典文献,并初步探索运筹学的一些发展轨迹,在CiteSpace软件中选择TimeLine时间线视图,可将共引文献的关系及聚类以时间轴的形式表现出来,方便观察知识的演化过程,运筹学的时间线图谱如图3所示。其中聚类表示的是高频引文,连线表示的是他们之间的被引关系。

图3 运筹学引文共现时间线图谱
从图3中我们可以看出运筹学经典文献出现的第一个高峰期是在20世纪50年代,通过查阅运筹学的发展历史可知运筹学产生于19世纪30年代,一直属于军事机密,到19世纪50年代,运筹学的发展迎来了第一个黄金期,英美等国相继成立了运筹学协会,从图中的节点中可以看出,这段时间产生的成果主要有1951年Kuhn和Tucker提出的K-T条件,在非线性约束问题的求解上做出了重要贡献[8]。1959年Dantzig总结的单纯形法为求解线性规划问题提出了一个有效的方法[9]。19世纪60年代,产生的主要成果有1960年Gilmore 提出的将线性规划运用于套材下料的问题[10]。1962年Ford J R提出的网络流问题等[11]。七十年代之后,较重要的研究已在前面有所论述。
在CiteSpace软件中,这些高被引的引文节点共同构成近些年来学科发展前沿的基础知识,在学科发展中起着重要作用。
2.3 运筹学发展的热点领域研究
在CiteSpace软件中学科研究热点表现为在某一段时间内某些引文呈现突增性,表示这一段时间内,这些引文的受关注度有所提高,构成学科的研究热点。在软件中引文的突增性用Brust值表示,Brust值越高,引文的突增性越强。

表2 运筹学引文突增性情况表
表中列出了一些高Brust值高的,首先考虑突增性排名第一的是Bierwirth C在2010年发表的《A survey of berth allocation and quay crane scheduling problems in container terminals》,该文章主要对于集装箱码头的泊位分布和岸桥调度做了一定的调查分析。文章的引用变化如图4所示,可以看到,文章在最近三年的被引用次数有了较大的增长[12]。
另外一篇突增性较高的文章是Stahlbock R在2008年发表的《Operations research at container terminals: a literature update》,文章也介绍了集装箱码头作业调度的一些方法,在重要文献中也已有过介绍。其引文频次的变化如图5所示。
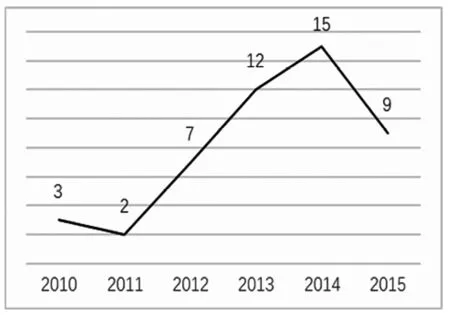
两篇文章近几年的引用频次都有了较大提高,两篇文章的施引文献主要有Akyuz M H在2014年发表的文章《A mathematical formulation and efficient heuristics for the dynamic container relocation problem》,作者在文章中提出了三种启发式算法解决集装箱运输问题,并对这三种方法做出了比较[13]。另外一篇施引文献是Alessandri A在2008年发表的《Modeling and Feedback Control for Resource Allocation and Performance Analysis in Container Terminals》这篇文章提出海运码头集装箱流动队列的动态离散模型,并对模型中资源分配的两个反馈控制策略进行说明[14]。大量的施引文献也说明,近些年来运筹学在集装箱码头的管理、仿真、优化与调度方面的运用已经成为该学科的一个研究热点。第三个Brust值变化较大的点出现在Rosenhead J在2001年发表的 《Rational Analysis for a Problematic World Revisited: Problem Structuring Methods for Complexity, Uncertainty and Conflict》,该文通过具体实例,讲解了一些解决不确定性决策建模的结构性方法[15]。但从引文分析的图谱上看,引文虽然波动较大,但总体平稳,15年以后对这些领域的研究有上升趋势,并不能看出明显的热点领域。

图6 罗森海德被引频次变化图
另外,其他节点并没有呈现出优势明显的突增性,发展研究比较平稳。这里就不再作过多的分析。
2.4 运筹学的研究前沿分析
对于前沿问题的研究,CiteSpace软件是通过对施引文献中相关内容的聚类得出来的,Citespace可以提供对文献主题,关键词,以及摘要的聚类,可以在软件面板中选择,本文选择文献中的主题词进行聚类,选择对数似然法抽取文献中的主题词,可以得到如图7所示的分析图谱
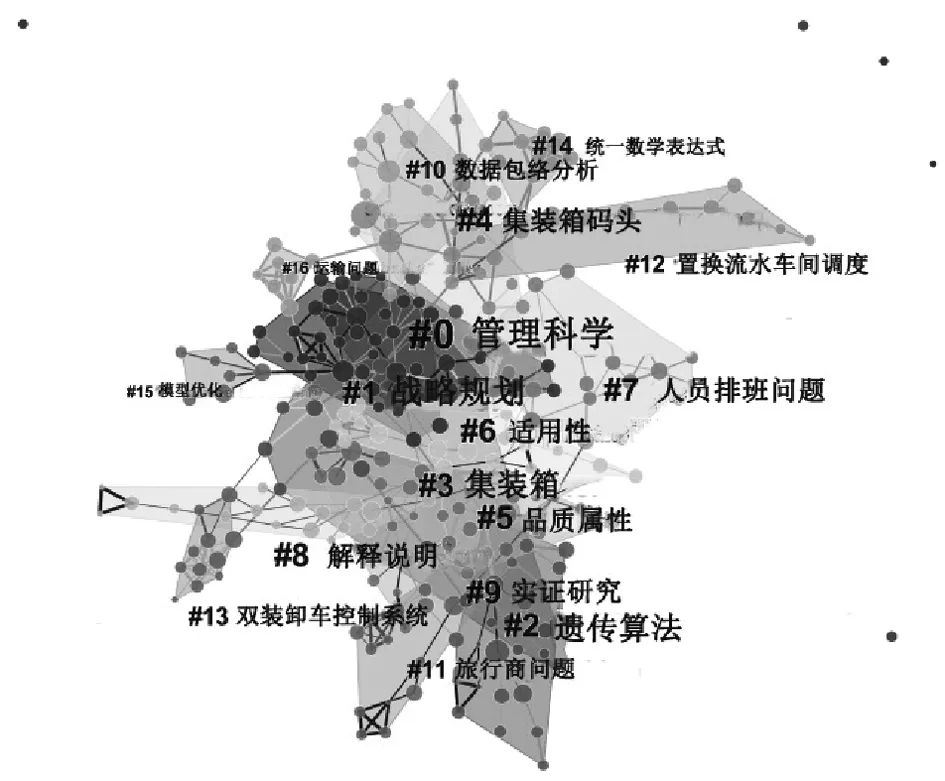
图7 知识前沿聚类图谱
从聚类图谱中可以看到,运筹学在管理科学领域的研究依然是最前沿的研究领域之一,运筹学在诞生之初就是为了给管理决策提供更好的决策方法,使管理活动更加科学化,一直以来运筹学在管理科学领域的应用就是重点研究内容之一。第二个前沿领域是研究战略制定与战略规则,面对不确定的外部环境,如何有效地进行模拟仿真,制定合理的发展战略也是运筹学研究的前沿领域之一。这方面的研究主要有Burt G在2011年发表的《Towards the integration of system modelling with scenario planning to support strategy: the case of the UK energy industry》中提出了支持不确定性的探索的系统建模集成方案规划,探索了如何利用情景规划提高组织战略制定的能力[16]。第三个研究前沿领域是遗传算法,这方面的主要研究有2008年张继军等发表的《Solving TSP with improved multi-Agent genetic algorithm》,文中提出了一种基于智能体对环境感知与反作用能力的新的函数优化方法来解决旅行商问题,具有很快的收敛速度,尤其是在优化超高维函数时更显示出了它的优越性[17]。另外还有Bogdanovic M等在2010年发表的《an ilp formulation and genetic algorithm for the maximum degree-bounded connected subgraph problem》研究了遗传算法在解决最大连通子图问题中的应用[18]。第四个研究前沿是对于集装箱码头的运输优化研究,这也是近几年来研究的一个热点问题,前面已经在热点研究中做出了一些相关论述。另外还有一些研究前沿领域,包括定性与定量相结合、人员的排班问题、数据包络分析等问题。
3 结论
本文通过citeSpace软件对于近十年来运筹学领域的部分相关文章进行分析发现:目前美国在运筹学研究领域依然遥遥领先,英国、中国等也取得了较为丰硕的成果。对近十年运筹学发展有较大影响的成果主要有Stahlbock R在2008对运筹学在集装箱运输领域,如港口的作业组织和控制,码头运作计划和调度的数学解析法、仿真方法、智能优化方法等的总结概括。19世纪70年代和80年代由Charnes A和Cooper W W以及Rhodes E开创的CCR模型和BCC模型。1979年由Garey M R总结的具有三百个具有NP完全性的问题,由Goldberg在1989年对于遗传算法的论著等。这些论著和其他一些重要文献共同构成了近些年来学科发展的基础知识。研究热点领域主要集中在运筹学在集装箱码头调度运输方面的研究。研究前沿主要有管理科学、战略制定、遗传算法、人员排班、数据包络分析等问题。
