不确定环境下基于时间、费用及鲁棒性权衡的多目标项目调度优化

李 雪， 何正文， 王能民

(西安交通大学 管理学院，陕西 西安 710049;过程控制与效率工程教育部重点实验室(西安交通大学)，陕西 西安 710049)

0 引言

项目调度问题(project scheduling problem，简称PSP)研究从时间和资源等条件上合理安排调度项目的活动，在资源最优利用的同时实现既定目标的最优化[1]。在实际项目调度中，工期和成本[2]与项目的交付及收益息息相关，是项目管理者普遍关注的重要指标，并且二者之间存在制约关系。此外，在现实情况中，进度计划常常受到一些不可控因素的干扰，如返工、机器故障等，从而导致项目无法按期交付。因此，在制定项目计划阶段考虑时间/费用之间权衡的同时，将这类不确定因素纳入其中是至关重要的[3]。项目计划的时间、费用和抗干扰能力在给定的资源、工期和预算等条件下是相互关联、相互影响的，单一指标的优化可能会导致其他指标的劣化，无法有效指导项目管理实践。在项目调度中同时优化上述三方面指标，可以使得经过多方权衡制定出的进度计划不但工期短、费用低，还具有更强的抗干扰能力。

由于项目管理在根本上是具有多目标属性的，项目调度中多目标权衡的相关问题吸引了大量国内外学者的关注。项目管理中，通过增加额外费用来加速项目执行过程中的某些活动，以达到缩短项目工期的目的，就是项目调度中经典的双目标问题——时间/费用权衡问题(time/cost trade-off problem，简称TCTP)。Demeulemeester和Vanhoucke[4]研究了确定性环境下的离散时间/费用权衡问题，并采用精确算法求解。Deckro等[5]使用非线性函数描述时间与费用的关系，研究连续的时间/费用权衡问题。Erenguc等[6]研究多模式条件下的资源约束型时间/费用权衡问题，采用分支定界算法求解并进行算例测试验证方法的有效性。Hazlr Ö等[7]以最小化完工时间为目标，使用基于分解策略的精确算法求解大型项目的离散时间/费用权衡问题。

确定性环境下的项目调度研究成果丰硕，近年来，不确定环境下的相关研究也得到了广泛的探索。Van De Vonder等[8]研究了资源约束下质量鲁棒性(工期)与解的鲁棒性(稳定性)之间的权衡。其中，鲁棒性是指当系统存在不确定影响因素时，仍然能够保持正常工作的特性，即系统所具有的抵抗不确定性干扰的能力[9]。Ke等[10]构建了随机环境下的时间/费用权衡模型，运用混合智能优化算法求解。何正文等[11]探讨了随机活动工期下的鲁棒性最大化问题，对比了三种启发式算法的满意解质量。庞南生和孟俊姣[12]创建项目鲁棒调度生成机制，构建工期最小化和鲁棒性最大化的双目标优化模型，并采用启发式算法求解。寿涌毅和王伟[13]使用遗传算法求解活动工期不确定的鲁棒调度优化问题，有效应对了活动工期不确定所产生的随机差异。何立华和孔云霄[14]考虑活动的延期风险，构建以加权时差最大化为目标的鲁棒优化模型，然后使用改进的启发式算法求解。Herroelen和Leus[15]构建了在特定工程环境下生成基准进度计划的数学模型，利用期望实际进度与计划进度偏差的加权和作为稳定性的衡量指标。此外，王杜鹃等[16]研究了单机环境下的多目标优化问题，从Pareto优化角度求解，改进经典的NSGA-II，提升算法求解效率。刘士新和宋健海[17]将模糊多目标资源约束调度问题转化为单目标组合优化问题，采用遗传局域搜索算法求解获得有效解集。

基于以上事实，本文研究不确定环境下基于时间、费用及鲁棒性权衡的多目标项目调度优化问题，在可更新资源(renewable resource)的约束下，以工期、鲁棒值和成本为优化目标确定项目各活动的开始时间，制定进度方案。在本文的后续部分，首先界定研究问题并定义相关变量，构建问题的多目标优化模型，将模型分解成三个子模型分析目标间的权衡关系；然后设计非劣排序遗传算法，提出三种针对性的优化策略，形成优化改进的非劣排序遗传算法；随后进行算法测试和参数的敏感性分析；接下来求解一个项目实例，得到非劣解集，并且变换资源组合对结果进行敏感性分析；最后总结全文并给出研究结论。

1 模型构建

1.1 问题界定

本文使用AoN(activity-on-node)网络G=(N,A)表示项目，其中N为节点集合，N={0,1,…,n,n+1}，A为有向弧的集合；节点表示活动，有向弧表示活动间的逻辑关系。为了表示方便，活动0和活动n+1均是人为添加的虚拟活动，分别表示项目的开始和结束，持续时间为零且不占用任何资源，活动一旦开始便立即结束。项目实施需要K种可更新资源，单位时间内第k(k=1,2,…,K) 种资源的可用量为Rk。活动i(i=0,1,…,n+1)的持续时间为di，活动i执行时对第k种资源的需求量为rik，活动i延迟单位时间所造成的成本损失为wi。第k种资源在单位时间内的单位占用成本为ck，项目最大工期为D。假设项目从零时刻开始执行，所有活动不能中断，且活动只能在给定的资源和时间条件下进行。

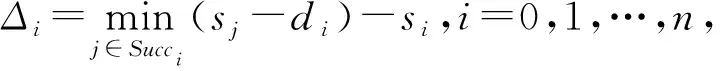
在项目实施过程中，项目工期是业主和承包商共同关心的一个重要指标。前面定义了各个活动的开始时间si，以及持续时间为零的虚拟结束活动n+1。由此，项目工期目标函数可以用虚拟结束活动的开始时间表示，即：T=sn+1。

项目工期T、项目鲁棒值Robu和项目成本C的表示式之间存在制约关系：Δi与项目工期密切相关，工期越宽松，活动之间就可以添加更多的自由时差，Δi也就越大；与此同时，项目鲁棒值Robu和项目成本C的表示式中均含有Δi，自由时差的变化直接影响鲁棒值和成本。自由时差由决策变量si计算得到，决策变量发生变化时，各目标值也随之变化。工期较宽松时，自由时差也较大，鲁棒值和成本就相对较大；而工期相对紧张时，自由时差则会较小，鲁棒值和成本也相对较小。本文中，我们考虑多个目标间的相互影响然后进行权衡优化，从而获得问题的满意解。

综上，本文的研究问题可以界定为，在给定条件下确定各活动开始时间si，以T最小化、Robu最大化且C最小化为目标，同时优化项目的工期、鲁棒值和成本三个指标。

1.2 优化模型

根据1.1中对研究问题的界定，以工期最小化、鲁棒值最大化、成本最小化为目标，以资源、优先关系为约束条件，构建基于时间、费用及鲁棒性权衡的多目标项目调度优化模型，表述如下：

minT=sn+1

(1)

(2)

(3)

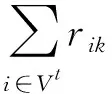
(4)

si+di≤sj,j∈Succi;i=0,1,…,n

(5)

(6)

si为非负整数,i=0,1,…,n+1

(7)

其中，Vt为t时刻正在执行的活动的集合。

上述多目标优化模型中共包含三个目标函数，两个约束条件，活动的开始时间si为决策变量。目标函数式(1)表示工期最小化，虚拟结束活动n+1的开始时间sn+1等于项目工期T。目标函数式(2)表示鲁棒值最大化，这里使用项目中各活动的自由时差加权和表示整个项目的鲁棒值。目标函数式(3)表示成本最小化，用项目实施过程中所占用资源的总费用作为项目成本。式(4)表示资源约束，保证项目执行过程中各类资源的使用量不超过相应资源的可用量。式(5)表示活动间的优先关系约束，保证当前活动结束后其紧后活动再开始执行。式(6)是用活动开始时间求自由时差的计算式。式(7)则为决策变量si的定义域。在多目标优化模型中，确定各活动的开始时间si就形成一个进度计划方案，每一进度计划方案对应确定的工期、鲁棒值和成本，改变决策变量可以使得目标函数值发生变化，然后通过目标值的比较、权衡和选择就可以达到多目标优化的目的，获得工期短、鲁棒值大且成本低的进度方案。

1.3 基于模型分解的三目标权衡关系分析

为了进一步研究1.2中构建的多目标优化模型，将原优化模型分解为如下三个子模型进行深入分析讨论：工期约束下的鲁棒值和成本的权衡，鲁棒值约束下的工期和成本的权衡，以及成本约束下的工期和鲁棒值的权衡。将原多目标优化模型分解为三个双目标子模型，目的是深入分析目标间的权衡关系，寻找优化多目标问题求解过程的有效方法。

1.3.1 工期约束下的鲁棒值和成本的权衡

将多目标项目调度优化模型中的工期函数转化为约束条件，就形成了工期约束下的鲁棒值和成本的权衡子模型，表述如下:

其中D*表示给定的最大工期。

该子模型中已将工期函数转化为不等式作为约束条件，在给定的工期约束下对鲁棒值和成本进行权衡优化。观察子模型中的两个目标函数可以发现，鲁棒值和成本中都包含以开始时间si计算得到的自由时差Δi，改变决策变量能够使得活动的自由时差Δi发生变化。保持式(3)的成本值不增加，在权衡过程中，最大化鲁棒值就是寻找CIWi和Δi的最佳搭配，也就是将自由时差优先分配给CIW值大的活动以增加项目整体的鲁棒性。但是当改变CIWi和Δi的搭配已经无法得到更大的鲁棒值时，就需要增加Δi来进一步增大鲁棒值，而观察成本目标函数可以发现，此时的成本必然会随之增加。也就是说，在一定限度内，权衡可以在保持成本值不劣化的情况下优化鲁棒值，但是超过限度后提高鲁棒值会使得成本上升，权衡就要在鲁棒值和成本之间进行取舍。保持式(2)的鲁棒值不降低，最小化成本就是寻找(ck×rik)和(di+Δi)的最佳搭配，也就是将自由时差优先分配给占用资源成本小的活动，从而降低项目成本。同样地，当二者搭配无法得到更低的成本时，就需要降低以减小成本，但是同时会导致鲁棒值的降低，过度的缩减成本是要以降低鲁棒值为代价的，此时的权衡需要在鲁棒值和成本之间进行取舍。

从上述分析可以发现，鲁棒值和成本两个目标的优化需要进行权衡取舍：在一定范围内，提高项目鲁棒值会造成成本的上升，降低项目成本会导致鲁棒值的降低。在决策变量变化的过程中，寻找两目标值的均衡点，可以达到对二者的权衡优化。

1.3.2 鲁棒值约束下的工期和成本的权衡

在项目调度中，工期和成本是两个重要的优化目标，时间/费用权衡问题优化的目标是实现二者的均衡。鲁棒值约束下的工期和成本的权衡子模型表述如下：

minT=sn+1

(1)

(3)

(9)

式(4)、(5)、(6)、(7)

其中Robu*表示给定的鲁棒值下界。

将原优化模型中的鲁棒值函数转化为约束条件，就得到了如上所示的鲁棒值约束下的时间/费用权衡优化模型。在该子模型中，同时最小化工期和成本两个目标，进行时间/费用的权衡。模型中，工期T与自由时差Δi直接相关，工期较大时，活动之间的空余时间会增加，自由时差Δi也更大，资源占用量增多从而使得成本增加，反之工期较小时则成本降低。由以上分析可见，工期和成本是同增同降的关系，该子问题优化的目标是在满足约束条件的基础上实现二者的共同优化。

1.3.3 成本约束下的工期和鲁棒值的权衡

将原优化模型中的成本函数作为约束条件，就可以得到成本约束下的工期和鲁棒值的权衡子模型，表述如下:

minT=sn+1

(1)

(2)

(10)

式(4)、(5)、(6)、(7)

其中C*表示给定的成本值上界。

该子模型是在满足成本约束的条件下，最小化项目工期、最大化项目鲁棒值。保持式(1)的工期不增大，在权衡过程中，寻找CIWi和Δi的最佳搭配以增加项目整体的鲁棒性。但是当改变CIWi和Δi的搭配无法再得到更大的鲁棒值时，就需要增加Δi来增大鲁棒值，这时会导致项目工期延长，权衡需要在工期和鲁棒值之间进行取舍。也就是说，在一定限度内，可以在保持工期不延长的情况下优化鲁棒值，但是超过限度后提高鲁棒值会使得工期延长。再者，工期较宽松时，有利于更好地安排自由时差，使项目具有更大的鲁棒值。由此可知，工期目标和鲁棒值目标在权衡过程中同样需要取舍，在决策变量变化过程中寻找二者的均衡点，可以实现工期和鲁棒值的权衡优化。

这里我们将多目标优化模型分解为三个双目标子模型，分别分析了三个目标间的权衡关系。基于以上分析结果，进行多目标优化时将问题转化为三个子模型，分别进行优化获得结果后反馈给多目标模型，有助于加快算法的收敛速度、提高满意解的生成效率。

2 算法设计

在模型分析时，将多目标优化模型转化为时间/费用权衡问题子模型，已有研究证实时间/费用权衡问题是一类NP-hard问题[19]，所以本文研究的多目标权衡优化问题是一个NP-hard问题。考虑研究问题的这一特性，应用智能优化算法求解多目标优化模型。首先给出求解该问题的遗传算法流程，然后针对研究问题设计两种优化策略，分别是选择性复制时的精英保留策略以及基于子模型权衡关系的优化策略，将两种策略与遗传算法有效结合，以此加速算法的收敛过程、提高运算效率，形成优化改进的非劣排序遗传算法NSGA-Ⅱ(non-dominated sorting genetic algorithm Ⅱ)。

2.1 算法流程

考虑研究问题的特点，采用遗传算法求解多目标优化模型，算法流程框架如图1所示。

图1 算法流程图

接下来对流程图中所示遗传算法的关键环节进行具体介绍。

1)解的表示

在算法中，一条染色体由活动的有序列表和自由时差列表组成。活动有序列表是对项目中各活动按照优先关系顺序排列而得，使用SSGS(serial schedule generation scheme)方法可以将其转换为一个可行的项目进度计划，同时保证活动的排列满足项目网络关系。自由时差列表指出为有序列表中的哪些活动添加自由时差以及自由时差值为多少。由此可见，活动有序列表及自由时差列表共同决定项目各活动的开工时间。

2)适应度的计算

由于研究的是多目标问题，无法直接将目标函数值转化为个体的适应度。这里采用非劣排序方法(后文2.2将进行详细介绍)，判断个体的优劣，将当代种群的所有个体按照优劣依次排序，排序越靠前，适应度也就越大，越有机会遗传进入下一代而被保留下来。

3)交叉操作

在交叉操作时，为了保证交叉后得到的个体仍然满足项目网络关系，采用一种适用于遗传算法的MUCOX(multi-component uniform order-based crossover)交叉算子实施交叉操作。该方法主要应用于项目调度问题的相关计算中，在针对存在优先关系约束的染色体进行交叉操作时，会同时考虑活动之间的优先关系，保证交叉后的染色体满足父代的优先关系要求。

4)变异操作

遗传算法的染色体包含两组基因：活动有序列表和活动的自由时差列表。在交叉操作中已经对活动的顺序进行了调整，而且活动的变异意味着要调整有序列表中的活动顺序，这样容易破坏活动间的优先关系，失败率较高。所以，此处对自由时差列表进行变异操作，即随机选取某个活动，将其自由时差随机增大或减小，从而获得变异个体。

5)子代种群的生成

在生成新一代种群时，主要运用四种操作：选择性复制、交叉、变异以及基于子模型权衡关系的优化操作(后文2.4将进行详细介绍)。以上四种操作分别形成一定数量的个体，共同形成新一代种群。

2.2 非劣排序

在求解多目标问题的遗传算法中，如何计算个体的适应度、判断可行解的优劣是一个难点，本文在计算适应度时采用非劣排序的方法。对于随机选取的两个染色体，使用如下步骤判断二者的优劣：

步骤1比较两个体S1和S2对应可行解的工期、鲁棒值和成本，工期短、 鲁棒值大、成本低的个体更为优秀。若个体S1(或个体S2)的工期短、鲁棒值大而且成本低(至少有一个目标函数值不相等)，则个体S1(或个体S2)支配个体S2(或个体S1)，个体S1(或个体S2)排序在前。其他情况则转步骤2。

步骤2当比较三个目标函数值无法判断两个体的优劣时，即个体S1(或个体S2)既有目标函数值优于个体S2(或个体S1)又有目标函数值劣于个体S2(或个体S1)，两个个体不存在支配关系。这时采用比较拥挤度的方法进行选优排序。首先对种群中的个体按照三个目标值分别进行排序，每个个体的单一目标值的拥挤度就可以表示为与其排序相邻的两个个体相应目标值之差，再将三个目标值的拥挤度经过归一化处理累加起来就得到了该个体的拥挤度。拥挤度大的个体，周围个体分布较为稀疏，为了增加种群的多样性，这里约定拥挤度越大，个体越优秀。通过比较两个体的拥挤度可以判断不存在支配关系的个体S1和S2的优劣，拥挤度大的个体排序在前。

为了进一步说明非劣排序的方法，表1给出了一个含有五个个体的种群。在对个体S1和S2排序时，首先对比二者的三个目标值。相对于个体S2，个体S1的工期短、鲁棒值大而且成本低，由此可以判断出个体S1支配个体S2，个体S1排序位于个体S2之前。在对个体S1和S3排序时，同样先对比二者的三个目标值，发现相对于个体S3，个体S1的工期虽然短，但是鲁棒值小而且成本高，二者不存在支配关系，无法直接判断优劣，需要计算两个体的拥挤度。使用步骤2中的方法计算可以得到个体S1和个体S3的拥挤度分别为1.475(30/50+400/800+3000/8000)、1.275(20/50+400/800+3000/8000)，个体S1的拥挤度更大，排序位于个体S3之前。

表1 非劣排序示例

2.3 精英保留策略

在进行选择性复制操作时，采用精英保留策略。已有模拟计算说明了如果将种群个体全部替换会使得当前最优解发生遗失，所以应该强制当前最优解遗传到下一代。具体操作步骤如下：

步骤1计算当代种群个体的工期、鲁棒值和成本，然后依据2.2中的非劣排序方法确定支配关系、计算拥挤度，判断个体间的优劣并进行排序。

步骤2按照步骤1中的优劣次序，选择种群中排序靠前的部分个体作为“精英”直接进入下一代。

采用精英保留策略使得当代种群中的优良个体直接遗传进入下一代，可以保证在每代之间最优秀的个体都可以被保留下来，确保遗传算法随着遗传代数的增加会一直收敛逐渐靠近最优解。

2.4 基于子模型权衡关系的优化策略

在完成选择性复制、交叉和变异等操作后，为了进一步优化求解过程，采用基于子模型权衡关系的优化操作。在子模型权衡关系的分析过程中，将多目标调度优化模型分解成了三个子模型。这里给出基于子模型权衡关系进行优化的步骤：

步骤1计算当代所有个体的工期、鲁棒值和成本。

步骤2对于工期最小的个体，将当前工期值作为上界，使用1.3.1中给出的子模型进行鲁棒值和成本的权衡优化，然后将优化后的个体放入子代种群中。

步骤3对于鲁棒值最大的个体，将当前鲁棒值作为下界，使用1.3.2中给出的子模型进行工期和成本的双目标优化，然后将优化后的个体放入子代种群中。

步骤4对于成本最低的个体，将当前成本值作为上界，使用1.3.3中给出的模型进行工期和鲁棒值的权衡优化，然后将优化后的个体放入子代种群中。

基于子模型权衡关系的优化策略在遗传算法中用于生成子代个体，即在算法流程中变异操作之后进行，生成一定数量的子模型优化个体放入子代、作为子代种群的一部分。

3 算法测试

为了验证本文所采用的精英保留策略和基于子模型权衡关系的优化策略对于算法性能的改善效果，设计三个版本的算法进行测试，分别是非劣排序遗传算法NSGA-Ⅱ，基于子模型优化策略的NSGA-Ⅱ，基于子模型优化策略、无精英保留策略的NSGA-Ⅱ，将三个版本的算法分别记为V1、V2和V3。在测试中，为了使算法具有同样的比较基准，为三个算法设置相同的终止条件。每个版本算法运行到指定迭代次数Itermax时终止，输出当前的非劣解集。

在生成算例时，按照表2设置参数，并采用ProGen[20]生成标准算例。表中“算例的非虚活动数N”、“项目截止日期D”和“资源可用量Rk”是要进行全因素试验的关键参数，将其设定几个水平以分析参数变化时对计算结果的影响。参数N有4个水平，参数D和Rk分别有3个水平，每种组合下生成10个算例，共获得10×4×3×3=360个算例。表2中其它参数按照项目调度构造惯例设定。

表2 ProGen的参数设置

对于算法求解得到的非劣解集所形成的近似Pareto前沿，可以通过计算其收敛度指标和分布性指标判断优劣。为此，我们首先将NSGA-Ⅱ运行若干代，将所有代际的非劣解集合并，保留其中的非劣解就形成了一个Pareto前沿参考解集P*。

计算第G代的收敛度值时，首先计算非劣解集中的点到参考解集间的欧几里得距离:

(11)

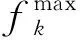
然后分别计算第G代非劣解集中各点的欧几里得距离，并取均值，再除以初始种群对应非劣解集的欧几里得距离均值进行归一化处理，以便于不同算例间的结果具有可比性。这样就计算得到了第G代非劣解集的收敛度值。收敛度值越接近0，就代表非劣解集越接近参考解集，算法的计算效果越好。

对于分布性指标，首先选取工期和成本组成的平面，将平面内的可行域范围划分成若干个小网格，对于一个网格若有非劣解位于其中，该网格即被占据，否则未被占据。接下来，统计第G代非劣解集所占据的网格数，再除以参考解集所占据的网格数进行归一化处理，就获得了第G代非劣解集的分布性值。分布性值越接近1，就表示非劣解集在近似Pareto前沿上分布越均匀，算法的计算效果越好。

为了评价算法的绩效，对比不同版本算法的优劣，定义如下三个指标：

·AT(s)：算法的平均计算时间；

·AC：算法的平均收敛度值；

·AD：算法的平均分布性值。

算法采用VC++编译器编程，在CPU主频为1.6GHz、内存为1.73GB的个人计算机上运行。取ρD=1.8、ρk=1.0对三个版本的算法进行测试，结果见表3。对比三个版本算法，从解的质量上看，算法V2的收敛度值AC绝大多数都小于算法V1的收敛度值AC，算法V2的分布性值AD绝大多数都大于算法V1的分布性值AD，说明基于子模型权衡关系的优化策略可以提升算法的收敛度和近似Pareto前沿的分布效果，但在项目活动较多、网络较为复杂时表现不够理想。算法V2的收敛度值AC均小于算法V1的收敛度值AC，算法V2的分布性值AD均大于算法V1的分布性值AD，说明精英保留策略能够显著提升算法收敛度和近似Pareto前沿的分布效果。从运算速度上看，三个版本算法的平均计算时间相差较小，说明增加两个策略后算法性能得到提升，运算速度却并未下降。

在最大截止工期取三个水平时(ρD=1.6，1.8，2.0)和资源取三个水平时(ρk=1.0，1.2，1.4)分别测试算法V2，进行敏感性分析，结果如表4、表5所示。表中ADmin、ACmin和ARmax分别为各活动数下算例的平均最小工期、平均最小成本和平均最大鲁棒值。

表4中，在最大截止工期的三个水平下，ADmin、ACmin和ARmax无明显差距，说明项目工期、项目成本和项目鲁棒值对最大截止工期不敏感。

表4 最大截止工期敏感性分析

表5 资源敏感性分析

表5中，在资源的三个水平下，ADmin随着资源的增加而变小，而ACmin和ARmax在不同资源水平下无明显差距，说明项目工期对资源变化十分敏感，增加资源投入能够缩短项目工期，但是随着资源投入的增多，缩短工期的效果会变差。项目成本和项目鲁棒值对于资源变化不敏感。

4 项目实例

4.1 项目背景及数据

LG住宅楼工程项目位于咸阳市高新开发区内，是咸阳力高地产·咸阳中华西路城市综合体西地块三期建设项目，占地面积40余亩，建筑总面积达11万余平方米。项目合同工期为650日历天，于2015年4月开始建设。图2为该项目的AoN网络图，共包含30个活动，其中活动0为虚拟初始活动，活动29为虚拟结束活动。

图2 项目网络图

项目每日可安排工作的操作工人共有355人，管理人员共有80人。各个活动的执行持续时间、资源需求量以及依据经验确定各活动的权重值等项目活动数据见表6。

4.2 进度计划安排

表6 LG项目活动数据

应用多目标模型和非劣排序遗传算法求解上述实例的调度优化问题。将带有两种策略的非劣排序遗传算法NSGA-II在CPU主频为1.6GHz、内存为1.73GB的个人计算机上运行，实现上述算法，运算过程中交叉概率取0.4，变异概率取0.1。根据表6输入LG住宅楼工程项目活动数据进行求解，经过计算获得指定迭代次数下的非支配解集，汇总项目各进度方案的工期、鲁棒值和成本数据结果见表7。

表7中程序运行得到了13个指定迭代次数下的非支配解。观察表格可以发现，每个进度方案所对应的三个目标值各有优劣。方案3、方案13的工期最短，为423天，但是鲁棒值较小；方案2的鲁棒值最大，为6029，但是工期和成本都最大；方案3的成本最小，约为1004万元，但是鲁棒值也最小。观察可得，没有一个进度方案的三个目标值都优于(至少有一个目标值不相等)其他方案，均为非支配解，决策者可以根据自己的需要和倾向性在非支配解中进行权衡、决策，选择满足自身要求的进度方案。

表7 进度方案计算结果

4.3 近似帕累托前沿曲面

为了更加直观地观察非支配解中工期、鲁棒值和成本三个目标的权衡关系，根据表7中的数据拟合出帕累托前沿的三维曲面如图3所示。

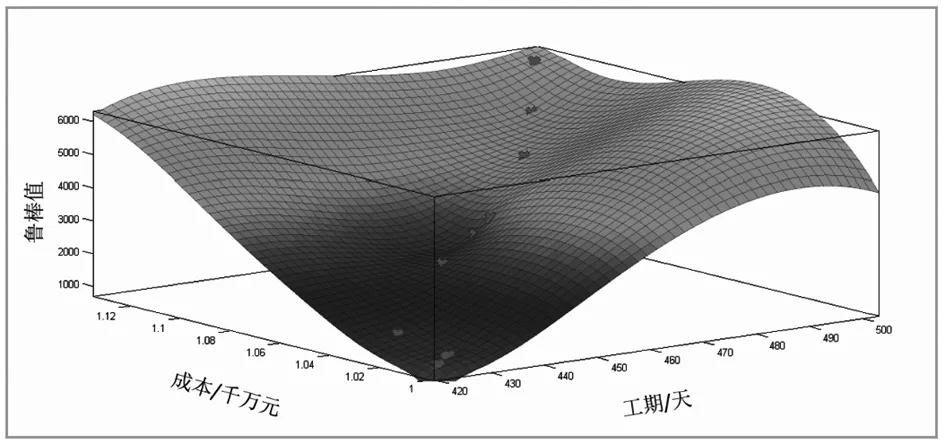
图3 帕累托前沿三维曲面

图3中标记点为表7中各进度方案所对应的点，它们共同形成了近似帕累托前沿，将其拟合成三维曲面就获得了帕累托前沿三维曲面图。观察图3可以发现，工期、成本较小时，鲁棒值也较小，当工期、成本都较大时，鲁棒值也更大。相对于三维曲面与三个坐标平面包裹范围内的可行解，帕累托曲面上的解工期更小、鲁棒值更大、成本更低，是更优的解。所以，工期、鲁棒值和成本的权衡优化在帕累托曲面上进行。

4.4 敏感性分析

在求解得到非支配解集后，为了进一步观察模型和算法在项目参数发生变化时，求解结果的相应波动情况，接下来变化资源组合对结果进行敏感性分析。

在LG住宅楼工程项目中，考虑了操作人员和管理人员两类可更新资源。下面，在三种资源组合情况下求解得到相应的非支配解集。如果同时观察三个目标的变化情况，难于分析目标之间的关系，为此我们分别将工期、鲁棒值和成本限定在一个较小范围内，逐对分析各目标对资源变化的敏感程度及其相互影响，相关数据结果如表8所示，三种情况下的敏感性分析变化曲线如图4～6所示。

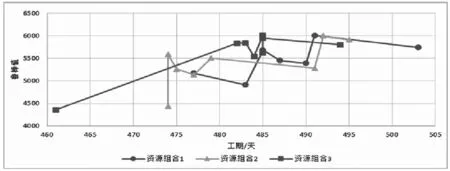
图6 工期、鲁棒值资源敏感性分析变化曲线

图4～6中资源组合1～3的资源可用量依次增大。在进行成本、鲁棒值敏感性分析时，不同资源组合下均选取了工期在440～460天之间的非支配解，形成图4。观察可以发现，成本较大的满意解鲁棒值也较大，与1.3.1中子模型分析的结果一致。而在三种资源条件下成本和鲁棒值的变化并不大，也就是说，将工期限定在一个较小范围内时，成本和鲁棒值对资源变化较不敏感。

在进行成本、工期敏感性分析时，不同资源组合下均选取了鲁棒值在2000～2500之间的非支配解，形成图5。观察可以发现，大部分成本较大的满意解工期相对也较大，与1.3.2中子模型分析的结果一致。而在三种资源条件下成本和工期的变化并不大，也就是说，将鲁棒值限定在一个较小范围内时，成本和工期对资源变化较不敏感。

表8 资源敏感性分析数据

在进行工期、鲁棒值敏感性分析时，不同资源组合下均选取了成本在1100～1150万元之间的非支配解，形成图6。观察可以发现，随着工期的增加鲁棒值呈明显上升的态势，与1.3.3中子模型分析的结果一致。工期相同时，资源充足的条件下满意解的鲁棒值更大，也就是说，将成本限定在一个较小范围内时，工期和鲁棒值对资源变化较为敏感。

综上，我们应用多目标模型和非劣排序遗传算法获得了项目实例的非支配解集，各满意解对应于不同的进度方案，它们在工期、鲁棒值和成本三个目标值方面各有优劣，决策者可根据自身对各指标的倾向性不同进行权衡取舍，选择工期短、鲁棒性大而且成本低的进度方案。此外，敏感性分析结果表明，充足的资源有利于缩短项目工期、提高项目鲁棒值。

5 结论

本文研究了不确定环境下基于时间、费用及鲁棒性权衡的多目标项目调度优化问题。作者首先明确了研究问题并对相关变量进行了定义，随后以工期最小化、鲁棒值最大化和成本最小化为目标构建了多目标项目调度优化模型，通过安排各活动的开始时间使得工期最小化、鲁棒值最大化且成本最小化。在此基础上，为了分析三个目标之间的权衡关系，将其分解为三个双目标子模型进行深入讨论，得到目标间的权衡优化关系。考虑到研究问题的NP-hard属性和多目标特点，设计非劣排序遗传算法求解多目标优化模型，使用非劣排序的方法确定个体间的优劣，并在算法中应用精英保留策略、基于子模型权衡关系的优化策略，设计不同版本算法在标准算例库上对两个策略进行测试，结果表明两个策略均可以提升算法的收敛度和近似Pareto前沿的分布效果。改变算例参数，发现增加资源投入能够显著缩短项目工期，但是随着资源投入的增加，缩短工期的效果会变差。最后，给出一个项目实例，计算得到非劣解集，拟合出近似帕累托曲面。此外，项目实例的资源敏感性分析进一步验证了子模型分析中目标间的权衡优化关系：成本和鲁棒值同增同减，相互制约；工期和成本同增同减，可以共同优化；工期和鲁棒值同增同减，相互制约。在制定进度计划时，决策者可以增加资源投入有效缩短项目工期、提高项目鲁棒值。本文的研究可以为多目标项目调度制定进度计划提供定量化决策支持。需要指出的是，本文所进行的研究未考虑活动的多种执行模式，仍有待进一步深入研究，未来可以向着多模式项目调度方向拓展。