具有Markov切换Cohen-Grossberg神经网络的依概率渐近稳定性①
2019-02-15吴媛媛余珮琳孙云霞
吴媛媛, 余珮琳, 孙云霞, 程 培
(安徽大学数学科学学院,安徽 合肥 230601)
0 引 言
Cohen-Grossberg神经网络[1](简称CGNN)是由Cohen和Grossberg于1983年首次提出的一种神经网络模型。 CGNN模型在模式识别、信号处理、最优化等方面都有广泛的应用,从而吸引很多的学者对其进行研究。在现实应用中,神经网络会出现随机故障,导致链接权值或阀值突然被改变,可能造成系统结构或者参数发生多样性改变,具有可变结构。 对于这种系统,常常利用Markov切换模型来刻画[2,3]。目前研究主要都集中于矩渐近稳定[4,5]和矩指数稳定。关于依概率稳定、依概率渐近稳定等方面的分析研究比较少见。 因此, 针对带有Markov切换的CGNN,我们将研究其依概率渐近稳性问题。 借助文献[2]中构造Lyapunov函数的思想,将基于Markov切换的转移概率的性质,构造一个特殊的Lyapunov函数,然后根据Lyapunov稳定性理论和LMI工具研究系统的稳定性。
1 准备知识
这里采用以下记号:Rn为n维欧氏空间,Rn×m为n×m实矩阵空间,I为适当维的单位矩阵,符号diag表示对角矩阵,λmax(·)表示矩阵的最大特征值,上标T表示向量或矩阵的转置, 符号*表示矩阵中的由对称性得到的元素,符号o(·)表示高阶无穷小。
令{r(t),t≥0}是完备概率空间(Ω,F,P)上的右连续Markov切换,取值于有限状态空间S={1,2,…m}。Γ=(γij)m×m是对应的生成元,满足
P{r(t+δ)=j|r(t)=i}=
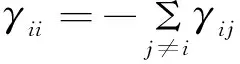
(1)
考虑如下带有Markov切换的CGNN:
(2)
其中x(t)=(x1(t),…,xn(t))T为n维神经元状态向量,
矩阵a(x(t),r(t))=diag(a1(x1(t),r(t)),…,an(xn(t),r(t)))为放大函数,b(x(t),r(t))=(b1(x1(t),r(t)),…,bn(xn(t),r(t)))T为神经元形为函数,Α∈Rn×n为连接权矩阵,g(x(t))=(g1(x1(t)),…,gn(xn(t)))T为神经元激励函数。

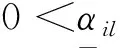
假设2 存在正常数βil,使得对∀x∈R, ∀i∈S以及l=1,2,…,n,有
xbl(x,i)≥βilx2。
假设3 存在正定对角矩
使得对∀x,y∈R
且x≠y以及l=1,2,…,n,有
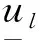
为了研究神经网络(2)的稳定性,假设g(0)=0,故神经网络(2)存在平凡解x(t)=0。
定义1 称神经网络(1)的平凡解是依概率稳定的,如果对∀ε>0,有
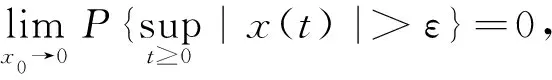
定义2 称神经网络(1)的平凡解是依概率渐近稳定的,如果它是依概率稳定的,并且有
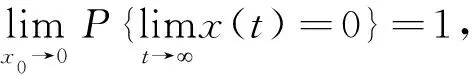
考虑带有Markov切换的一般的随机微分系统
(3)
其中f:Rn×S→n,假设系统(3)存在平凡解。对于任意二阶连续可微函数V(·,i),i∈S,关于系统(3)定义算子
V(x,i)=fT(x,i)
(4)
引理1[2]: 设D⊂Rn为包含原点的任一区域。 若对∀i∈S,存在满足下列条件的非负函数V(·,i):D→R:
(i)V(·,i)在D中连续,并且V(x,i)=0当且仅当x=0;
(ii)V(·,i)在D-{0}中二阶连续可微,且对于任意充分小的α>0和ε>0,有
LV(x,i)-κ, ∀ε 其中常数κ=κ(ε)>0,则系统(3)的平凡解是依概率渐近稳定的。 对于任意i∈S,记: 定理1 若存在常数μi∈R和正定对角矩阵Q,P∈Rn×n,使得对于∀i∈S有下面的矩阵不等式成立: (5) 证明: 定义列向量μ=(μ1,μ2,…μm)Τ∈Rm,令 Γc=μ+βΙm 有解c=(c1,c2,…,cm)∈Rm。 将上面的代数方程展开可得: (6) 进而由(6)式可得: (7) 选择常数θ∈(0,1)充分小使得 1-θci>0, ∀i∈S (8) 和 (9) 同时成立。 对于∀i∈S,定义Lyapunov函数 V(x,i)=(1-θci)|xΤQx|θ 对于神经网络(2),易算得由(4)式定义的微分算子 LV(x,i)=-2θ(1-θci)|xΤQx|θ-1xΤ Qa(x,i)[b(x,i)-Aig(x)+o(|x|)]+ (10) 由假设1 知对∀i∈S,放大函数a(x,i)满足 a(x,i)a(x,i) (11) 因此,将矩阵不等式(5)分别左乘和右乘矩阵diag(a(x,i),Ι),可得 (12) 由假设1和假设2知对∀i∈S,有 -2xΤQa(x,i)b(x,i) (13) 由假设3知对∀i∈S,有 gΤ(x)Pg(x)xΤUPUx (14) 将(7),(12)-(14)式代入(10)式可得,对于∀i∈S LV(x,i) 2xΤQa(x,i)Aig(x)+o(x2)]+ θ(1-θci)|xΤQx|θ-1[ξΤΦiξ+μixΤQx+ (15) 其中ξ=(x,g(x))T,O(x)→0(x→0)。 因此,对于∀i∈S,由(8)式知对于任意充小的α>0和ε>0,当ε LV(x,i)-κ(ε)<0。 由引理1可知神经网络(2)的平凡解是随机渐近稳定的。证毕。 定理2 若存在正定对角矩阵Q∈Rn×n,使得对于∀i∈S有下面的不等式成立: (16) 则神经网络(2)随机渐近稳定。 证明: 由(16)式知β>0。 注意到,由假设1和假设3知,对于正定对角矩阵Q∈Rn×n,有下式成立: 2xΤQa(x,i)Aig(x) 与定理1的证明类似可证,若不等式(16)成立,则神经网络(2)随机渐近稳定。 证毕。 探讨了一类神经网络的依概率渐近稳定性。基于Lyapunov稳定性理论,利用Markov切换转移概率的性质和线性矩阵不等式(LMI)工具。2 主要结果
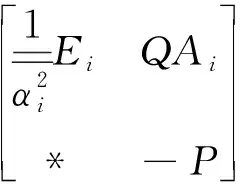

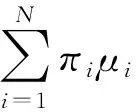
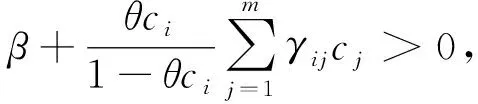
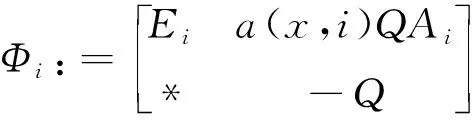
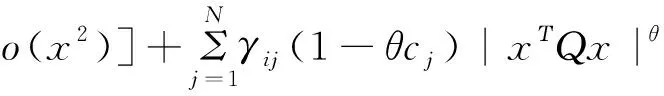
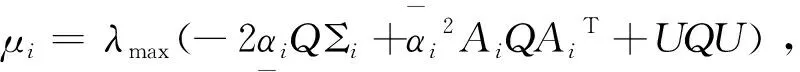
3 结 论
