基于半经验融合方法的锂离子电池剩余寿命预测①

陈亮亮

(同济大学 汽车学院, 上海 201804)

0 引 言

锂离子电池相比其它类型电池具有高功率密度和更长循环寿命的优势，因此被广泛应用于电动汽车和电网存储领域。然而随着电池的循环使用，由于活性材料的溶解、SEI膜的生长、电解液的分解以及电池内部材料晶体结构的变异，会导致其性能逐渐衰退，甚至导致危险事故发生。能够实现对锂离子电池的健康状态进行监测尤为重要。目前对电池剩余使用寿命预测主要分为机理模型和纯数据驱动模型。Popov等[6]提出一种通用的基于第一性原理的充放电模型来模拟电池循环性能变化且效果良好。White等[7]提出基于物理机理的单粒子模型模拟电池循环寿命衰减过程，提出分为三个衰减阶段并进行验证。陈雄姿等[8]使用一种贝叶斯最小二乘回归方法对比结果优于高斯过程回归方法。机理模型虽然能反映衰减机理，但是建立复杂数值求解困难；纯数据驱动方法则仅基于数据预测使用简单，但通用性不强难以适应电池衰减规律。通过对18650电池的寿命衰减实验基于高斯拟合建立寿命衰减模型，提出一种基于高斯拟合模型和粒子滤波算法的半经验融合预测方法，能够得到比较精确的预测结果，且模型简单参数较少，通用性较强。

1 粒子滤波原理

粒子滤波是一种基于蒙特卡洛仿真和贝叶斯估计的能处理非高斯非线性系统的滤波算法，通过对离散随机粒子的权值计算和重采样，不断迭代以逼近系统随机变量的概率分布。

1.1 贝叶斯估计

将研究的动态系统利用状态空间模型进行描述，某个时刻k的状态预测方程和观测方程如下：

(1)

贝叶斯滤波通过状态方程在已知上一时刻状态的基础上预测得到这一时刻系统状态先验概率密度，再由已知的实际测量值去修正计算出对应的后验概率密度。

当已知系统状态xk初始概率密度的值为p(x0|z0)=p(x0)，计算k时刻对应的后验概率密度的状态预测过程和更新过程如下：

预测：

(2)

更新：

(3)

1.2 蒙特卡洛抽样

蒙特卡洛抽样是将研究对象描述或构造成随机概率过程，从已知的概率分布中进行采样，随着样本增加实现模拟实验后，建立各种估计量将得到的无偏估计作为待解决问题的解。

如果已知先验分布且根据状态空间模型采样得到N个样本，可以通过下式近似计算得到后验概率密度分布：

(4)

(5)

1.3 粒子滤波计算过程

①在MATLAB中导入实验得到的4组锂离子电池寿命衰减数据，剔除其中的异常数据，基于高斯拟合方法建立状态预测模型和观测模型

②设定预测起始圈数为100圈，前100圈的数据为已知数据，利用已知数据进行MATLAB拟合得到三个未知参数的初值

③初始化算法中需要设定的相关参数，包括采样粒子的数目N，电池寿命终止时的阈值，过程噪声协方差Q的值以及观测噪声协方差R的值

④对粒子集以及权值进行初始化

⑤进行重要性采样，根据q(xk|xk-1,zk) 随机抽取样本N个

⑧更新滤波器滤波之后的状态，基于新的状态利用观测模型迭代更新电池容量的值，并得到容量的预测值

⑨判断电池容量是否已经达到寿命终止的阈值，若未达到继续执行算法预测过程⑤⑥⑦⑧，直到达到阈值结束整个预测过程，输出预测剩余使用寿命的圈数。

2 实验结果分析

2.1 实验步骤

实验使用三星 18650 三元锂离子电池，用深圳新威尔电池测试设备进行电池剩余使用寿命测试。

将实验电池放置到恒温箱中调整到室温(25 ℃)，利用电池夹具将电池正负极连接到新威尔充放电设备上，输入测试程序设定测试流程，具体测试步骤分为电池老化实验和电池容量标定实验两部分：

①电池老化实验：在室温下以大小为2 A的电流进行恒流充电，截止电压为4.2 V，然后在4.2 V电压下进行恒压充电，截止电流为26 mA(即为100%SOC)，静置1h，再以1.00 C恒流放电至截止电压2.75 V。

②电池容量标定实验：在室温下以大小为2 A的电流进行恒流充电，截止电压为4.2 V，然后在4.2 V电压下进行恒压充电，截止电流为26 mA(即为100%SOC)，静置1h，再以C/3恒流放电至截止电压2.75 V。重复2次，取2次测量放电容量的平均值作为电池放电标定容量。

每重复进行10次老化实验充放电过程，进行一次容量标定实验。不断重复直到达到电池寿命终止的阈值。

2.2 仿真及结果分析

通过对实验数据进行处理，利用MATLAB工具对锂离子电池容量衰减数据进行高斯拟合，得到表达电池随充放电循环容量衰减的高斯拟合公式：

C=R*exp(-((k-λ1)/λ2)2)

(6)

式中，C表示电池容量，K表示循环圈数，R表示随着充放电循环电池容量受到阻抗影响的因子，λ1和λ2表示电池容量受到电池性能衰减影响的因子。

假设这里的噪声均为均值为0，方差未知的高斯白噪声，得到预测模型的状态为：

X(k)=[R(k)λ1(k)λ2(k)]T

(7)

则状态方程如下：

(8)

观测方程为：

C(k)=R(k)*exp(-((k-λ1(k))/λ2(k))2)+ν(k)

(9)

测量噪声ν(k)为均值为0，方差为συ的高斯白噪声。

已知其中三个电池B1、B2、B3前100圈的数据，基于寿命衰减模型利用MATLAB软件进行拟合，将得到的三个未知参数的值取平均值作为B4电池退化模型的初值。

表1 B1、B2、B3模型参数

B4电池模型的初始值为：

通常所研究对象会不可避免地受到外界各种随机因素的影响，因此假设电池寿命衰减模型中的三个参数和容量Q均受到高斯白噪声干扰。将计算所得三个参数的初始值代入到公式(6)中得到初始容量衰减模型，导入B4电池的数据，在初始容量衰减模型的基础上利用B4电池已知数据进行迭代更新，在粒子滤波算法跟踪过程的迭代下得到B4电池的剩余使用寿命预测结果如下图所示。

图1 预测结果图：已知前100圈

图1表示已知前100圈电池放电容量数据，预测100圈之后的电池放电容量，并且基于此判断容量衰减是否达到电池寿命终止时的阈值，即按通常情况所认定的临界值(电池额定容量的70%)，计算输出剩余使用寿命的圈数。图1中蓝色实线表示B4电池在循环寿命衰减实验中随循环圈数累计放电容量衰减的实验测量数据，红色实线表示基于粒子滤波算法进行处理后状态更新计算得到的滤波估计数据，绿色实线表示基于前100圈已知数据进行初始状态空间模型迭代更新得到的预测数据，可以看出红色实线与蓝色实线保持比较好的一致性，即滤波估计数据与实验测量数据之间误差较小，表明粒子滤波算法展现出效果很好的跟踪能力。绿色实线对比蓝色实线可以看出具有不错的预测效果，图1和图2分别是以100圈和166圈作为电池剩余使用寿命预测起始点，以额定容量的70%作为阈值得到的寿命终止圈数为269圈，对比预测剩余使用寿命与真实测量剩余使用寿命结果如表2：

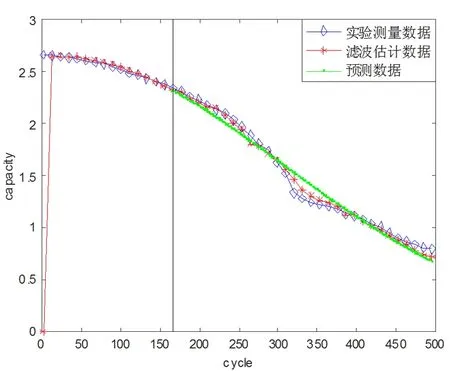
图2 预测结果图：已知前166圈

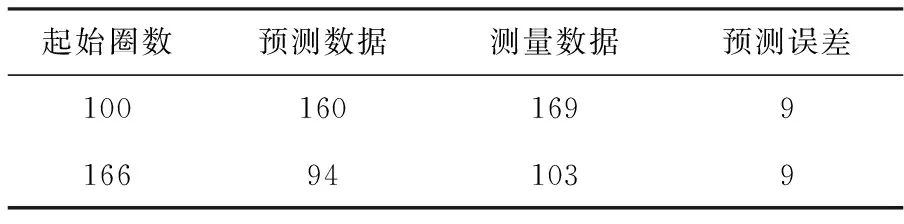
起始圈数预测数据测量数据预测误差1001601699166941039

由表2可知当预测起始圈数为100圈时粒子滤波算法预测得到的剩余使用寿命为160圈，而实际寿命衰减实验的测量数据为剩余169圈，剩余使用寿命的预测误差为9圈；当预测起始圈数为166圈时，算法预测得到的剩余使用寿命为94圈，实验实际测量得到的剩余使用寿命为103圈，预测误差为9圈。从中可以看出文中实现的预测方法具有良好的预测效果，在起始预测圈数分别为100圈和166圈时预测误差均小于5%。

3 结 语

通过对锂离子电池进行寿命老化和容量标定实验得到多组电池随充放电循环容量衰减数据，基于数据所建立的电池寿命衰减经验模型形式较简单、参数较少且能较好适应寿命衰减规律，利用融合方法得到的剩余使用寿命预测结果能达到小于5%的预测精度，表明文中提出的基于高斯拟合模型和粒子滤波算法的融合预测方法效果良好。