多目标粒子群算法在医院床位安排中的优化应用①
2019-02-15沈良生邓子龙
沈良生, 邓子龙
(安庆职业技术学院,安徽 安庆 246003)
0 引 言
医院床位的合理安排涉及医院床位利用率、医院效益和患者满意度等多个方面,是典型的多目标优化问题。针对床位资源的合理配置,学者们展开了大量研究,文献[1]从国家政策、医院管理、病人结构等方面讨论了医院床位的使用效率问题;文献[2]从医疗市场、疾病谱、医学模式、付费方式等几个方面,讨论了医院床位的配置标准;文献[3]建立了病人等待时间模型,将目标函数设置为最优平均等待时间,将病床安排具体模型化。上述实践多停留在定性层面或将病床安排等效成单目标规划问题,没有综合考虑医院和病人等多方需求。针对医院病床安排问题展开研究,将医院病床安排转换为多目标优化模型,并利用多目标粒子群算法加以求解。
1 医院床位安排问题建模
(1)床位安排的多目标优化问题
假设医院某科室空余床位N0张,现有n种病的患者排队住院,每种病包含患者的数量矩阵为M0,要求从这n中病人中,择优选出N0个病人入院。由于病情严重情况(不考虑急症需立即安排入院的情况),即使患相同疾病的患者住院时间及开销也会不同。设P0表示入住病人的已等待时间(天数)矩阵,V0表病人入院后的拟住院时间(天数)矩阵,C0表示病人住院期间的医疗保障支出。
衡量病床安排方案是否最优,要从医院和患者两方加以考虑。医院方面,通常以病床周转率来衡量病床安排的合理性,周转率最高,等效于病人的总住院时间最短;同时,医院还需综合考虑患者满意度,患者满意度主要与病人等待入院时间相关,即病人等待入院时间越长,入院安排的优先级越高。
因此,病床合理安排可归结为病人总住院时间最短和已等待时间最长的双目标优化。同时,医疗保障支出是院方与政府的经济支出,一次病床安排所需的医疗保障支出不宜过高,因此,可将一次病床安排所需的医疗保障支出作为限制条件。
(2)多目标背包问题模型
设计一种方案,将多种物品放入背包中进行运送,要求运送物品的总价值达到最大,总体积为最小,同时运送物品质量在一定的限制范围内,这就是多目标背包问题。假设物品的种类数为N,每一个种类包含的物件数为M,从每类物品中选取一个物件放入背包。待运送物品价值矩阵为P,体积矩阵为V,质量为C,选择矩为X。多目标背包问题可用下式描述:
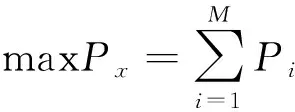
(1)
其中,P、V、X都是M×N的矩阵,Z表示对于背包的质量限制。
(3)病床安排与背包问题的转化
病床安排问题与背包问题有相似之处,但也存在差异,如床位数N0与病种数n之间并不匹配;安排病人时,不一定按患病种类进行挑选;每种病包含病人数不一定相同等问题,使病床安排问题不能套用背包模型求解,需进一步处理、简化。将病床安排问题转化为背包问题求解,可进行以下几方面简化:
(1)出于手术安排方便等原因,医院病床安排中常采用“异种病优先”原则[3],每次安排病床时,优先选择患不同病的病人,如眼科空余两张病床,白内障、眼科外伤各有若干患者等待入院,若一张病床安排了白内障病人,则另一张病床优先安排眼科外伤病人;
(2)床位数N0与病种数n不相等时,可直接假设N0=n,当N0小于n时,根据得到的选择方案,优先安排被选择的病人,被选择到但因床位数未安排的病人,可以确定优先级,优先安排至下一阶段空出病床中;而当N0大于n时,从N0张病床中选出n张病床,进行优化方案求解,再比较N0-n与n的大小,如(N0-n)>n则继续从剩余床位中选择n张进行床位安排,反之,则按照床位数小于病种数的情况进行求解;
(3)每种病包含的病人数不同,这会导致各矩阵各列包含的元素个数不同,这种情况下,将每种病包含的病人数按已等待天数进行排序,然后,设n种病中,包含患者数量最少的为第n0种病,包含患者数为a,则从各种病中,依据等待天数排序后,各选择a个患者,重新组成各个矩阵。
经过以上处理,病床的合理安排问题就可描述为,现有n种病的病患,每种病包含M0个病患,已知所有病患的已等待时间矩阵P0,拟住院时间矩阵V0,医保支出矩阵C0。要求从这n种病的病患中,各选择一个病患,在保证一定医保支出的前提下,使选择的病人已等待时间最长、总住院时间最短。这就将病床安排问题等效为背包问题进行求解。该问题可用公式表示为:

(2)
其中,P0、V0、X0都是的M0×n矩阵,Z0表示对于一次入院安排医保支出的限制。
2 经典粒子群算法
在经典粒子群算法中,所有粒子搜索时都要在限定区域内,并满足一定的限制条件。假设粒子在D维空间进行搜索,粒子数为m,则基本过程描述如下:
(1)初始化粒子位置、速度
随机初始化粒子的位置和速度,假设Xi=(xi1,xi2,...,xiD)是粒子i的初始位置;Vi=(vi1,vi2,...,viD)是粒子i的初始速度;
设集合Pi=(pi1,pi2,...,piD)为单粒子最优解,用来记录粒子i经历过的最好位置;设集合Pg=(pg1,pg2,...,pgD)为全体粒子最优解,用于记录所有粒子经历过的最好位置。从定义上可以看出,Pg中元素的值对应于Pi(i=1,2,...,m)中的最优值。
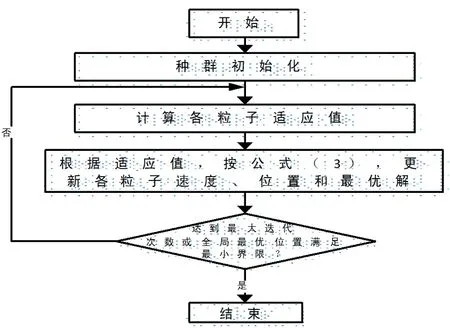
图1 经典粒子群算法流程图
(2)选择迭代更新策略
根据上述参数,更新位置、速度的公式为:
(3)
其中,d∈[1,2,...,D],w表示粒子当前时刻的状态受前一时刻状态的影响程度,即惯性权重;c1、c2为学习因子,一般取c1=c2;r1、r2为扰动系数,用来表示搜索的随机性,从而增大各粒子的遍历空间,其通常在[0,1]之间随机取值。
(3)更新最优位置
(4)设定停机准则
一般而言,寻优算法都要设定相应的停机准则,普遍遵从以下原则:
1)对迭代次数进行设定,使其达到规定次数;2)全局最优位置在连续规定的次数内没有变化;3)在连续规定次数内,全局最优位置的改善量不能大于或等于规定界限。
图1所示即为经典粒子群算法流程图。
3 多目标粒子群算法
多目标粒子群算法相较于经典粒子群算法,其目标函数为多个,应用时具有一定的局限性。为了解决在应用粒子群算法时的局限性问题,对算法进行了如下改进:一是假设在某次迭代后,某粒子的最优位置解不单一,存在多组非劣解,则历史最优解采取随机选择的方式从中择一而定;二是采取某种特定准则,在众多粒子的非劣解集中,确定某次迭代后的全体最优解,目前而言,根据“拥挤度”选择全局最优解是较常见的方法,通常情况下,为了保证能够最大程度的遍历所有未知区域,全局最优解要在不是特别“拥挤”的区域选择。确定各粒子“拥挤度”时,一般采用自适应网格法。
综上所述,多目标粒子群算法流程如下所述:
(1)对种群进行初始化,将搜索过程中发现的全局最优解的全体非劣解存储在某设定的非劣解集中;
(2)通过迭代、更新产生下一代粒子的位置,并存储在相对应的非劣解集中;
(3)通过筛选比较,从每一个粒子的非劣解集中选出历史最优解,进而确定全局最优解的非劣解集;
(4)不断重复(2)-(3),直至满足停机准则;
(5)将最终得到的非劣解集输出。
4 实例分析
为了验证多目标粒子群算法的优劣,下面将以医院床位安排为实例,分别利用多目标粒子群算法、加权法进行求解,并对结果进行比较。
参数设置:某医院眼科现有空余床位5张,现有白内障(单眼)、白内障(双眼)、青光眼、视网膜疾病、眼科外伤等5类疾病的患者等待入院,每类疾病排队等待的患者数量、已等待天数、拟住院时间以及估算的医保支出如表1所示,要求给出一种合理的病床安排方案,限制条件是一次病床安排医保支出不大于85000元。

表1 排队入院患者参数表
根据以上参数,已等待时间矩阵P0,拟住院时间矩阵V0,医保支出矩阵C0可分别表示为:
首先采取多目标粒子群算法对该问题进行求解。根据问题描述,设粒子维数为D=5,粒子数为M=50,最大迭代次数为N=200,在速度更新时,学习因子取值为c1=c2=0.8,惯性因子取值范围为最大值ωmax=1.2,最小值ωmin=0.1,每次迭代时,惯性因子的计算公式为ω=(ωmax-ωmin)×n/N,其中n表示当前迭代次数,根据以上设置参数进行求解,结果如下:

表2 多目标粒子群算法求解的病床安排方案
注:每一方案中,P0、V0、X0的列数分别对应五类疾病,每一类下选取1-4对应P0、V0、X0行数。
从表2可以看出,通过多目标粒子群算法求解,共得出20种医院床位安排方案,每种方案对应的病人已等待天数、拟住院时间如图2所示。

图2 非劣解集住院时间、等待时间的空间分布情况
根据图2可以看出,利用多目标粒子群算法能够得到多种病床安排方案,多种病床安排方案的非劣解集内所有点之间,一些在等待时间上占优势,一些在住院时间上占优势,决策者可以综合考虑各种情况,根据实际需求来进行选择。
针对同一问题,选取文献[6]中的加权法进行求解,设置目标函数为:


图3 加权法求取结果与多目标粒子群求取结果的比较
5 结 论
通过比较可知,利用多目标粒子群算法能够给出所有满足约束条件的病床安排方案的非劣解集,而运用加权法,需要不断重新调整权值进行运算,其不同权值下的解只是多目标粒子群算法中非劣解集的一个特例。因此,通过实例分析可以得出,采取多目标粒子群算法,能够更方便决策者综合考虑各种情况来进行决策,该算法更加有针对性,在实际应用中具有一定的参考价值。
