事故占道对城市交通影响的数学模型分析①

张博雅, 汤凤香

(佳木斯大学a.经济管理学院;理学院,黑龙江 佳木斯 154007)

0 引 言

随着社会经济的不断发展和人们生活水平的不断提高，人们的思维观念也在不断发生着巨大的变化。这种变化具体表现在人们出行所使用的交通工具上，从2017年的统计数据看，我国汽车保有量约为2亿辆，保有量占全球20%，销量占全球30%，而千人汽车保有量140台。人均汽车占有量的增多，导致了各种交通问题，造成了大量的生命财产的损失。事故占道，是交通事故发生过程中的一种车道被占问题[1]。总体来说，事故占道其实是指由于在城市等道路上发生各种交通工具引发的事故、路边正常或非正常的停车等等因素，从而使得车行通道的通行、运行能力在一定的时段内出现较大幅度的降低的现象。

交通流量密度大是当前的城市交通道路的主要特点，一旦一条或多条车道被意外占用，会大大减小当时路面的各个车道的运行能力，尽管发生的时间可能很短，但是也容易造成车辆排队的状况，从而导致交通阻塞，甚至会发生更加严重的状况。

事故占道的种类繁多，如果根据事故发生前后的统计数据，并结合适当的数学分析方法，是可以有效的判断出事故占道对城市交通运行的影响层次，进而为交通、运营管理等部门做出决策提供有利的保障。

1 事故占道的内在因素分析

由于交通事故的发生改变了道路和交通状况,从而导致了新的交通流特征，这种车辆运行表现为“跟—驰”现象[2]，也就是说，至少有两个汽车前后间距几乎达到了一个容许的最小长度，后车根据该最小间距并尝试以高于前方汽车驾驶速度行驶但不能超车。通过分析施工道路附近车辆的以下特征可知，当交通流密度较高时，车辆之间的空间相对较小，驾驶员只能以非自由状态进行“跟—驰”，亦即根据前车所能展现出来的信息控制好相对应的车速。

事故路段的通行能力是车流模型中的一个重要表征参数，可以根据及时标定该事故路段的运行能力、周边环境状况等，来初步判定车量的跟队长度以及跟队所需消耗的时间，同时尽快确定有效的方案进行交通疏导，结合有关资料，我们对事故路段通行能力的进行如下表征：

注：t1在该时刻发生事故；t2事故在该时刻结束；t3交通顺利疏导时刻；图中密集线段标注的三角形区域为车流密度过大导致的延误。

根据流量守恒方程及图中拥挤扩散过程，可以得到

其中nt为t时刻到达的交通流量(veh/h);ct为t时刻道路的通行力(veh/h) .当t20时，则交通受阻，车辆堆积，从而造成道路通行能力减弱，反之若nt-ct<0,其交通流入量在其最大通行能力范围内，则不会影响交通运行。当然，事故对运力的影响不仅取决于该事故发生地点的实际车道数，还取决于堵塞道路的车辆比例。

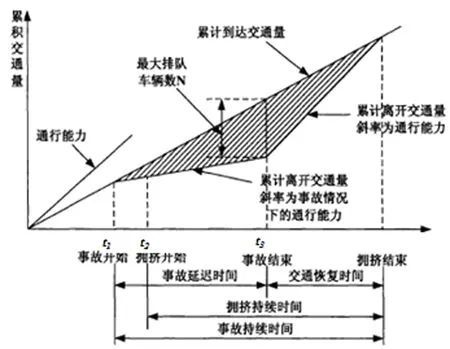
图1 断面分析

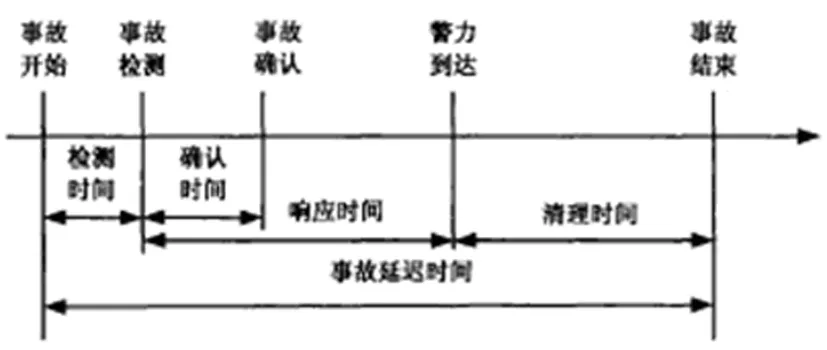
图2 事故分析

2 问题分析与模型建立

文中采用某地交通事故调研数据。

图3 交通事故位置示意图

2.1 问题分析

在堵车整个事件过程中，通过分析我们知道，由于路段发生事故，事故现场横截面的车辆通行能力小于进入上游路口的车辆交通流量，导致堵车，这是堵车排队问题的核心原因；事故持续时间越长，排队长度越长。所以因为该横截面实际交通事故而引发的路段车辆跟队长度与事故持续时段、路段上游车流量以及事故实际运行力有着必然联系。

在某时刻事故发生点至下游路口的总车辆数，与排队队伍里的车辆数与队伍后面剩下路段正常行驶车辆有关。而这些车辆之所以“堆积”，是与事故发生瞬间这段路面的正常的行驶车辆，以及在后续的时间里上游路口的流入车辆和事故点处横截面车流出车量有关。

由于实际交通行驶过于复杂，我们把上游流入车辆按匀速匀间距行驶，不考虑上游红绿灯的影响且题里涉及间距短，车速按m/s等计算来简化问题。

2.2 基本假设与符号约定

(1)在堵车排队的过程中，排队车辆两两之间的距离恒定且在三条车道上车辆分布长度情况一样。

(2)上游路口车辆均匀流入，且不考虑上游路口红绿灯的影响[4]。

(3)在堵车横断面前方适度范围内没有车辆拥堵现象，保证堵车横断面处其通行能力不受下游影响。

(4)车身长度按标准桑塔纳小轿车计算，且堵车段车辆间隔适度。

(5)车辆排队长度应不大于事故点到上游路口的距离。

(6)车辆数按标准车当量算。

L1——交通事故所影响的路段车辆排队长度(单位：m)

L2——撞车点距离上游路口的长度(L2=240m)

L3——车辆排队队尾距离上游路口的长度(单位：m)

Q1——事故横断面实际通行能力(单位：pcu/h)

Q2——路段上游车流流量(单位：pcu/h)

X1——标准桑塔纳小轿车的车身长度(通过相关资料查得X1=4.8m)

X2——堵车排队车辆适度间距(通过相关资料查得X2=0.2m)

t——事故持续时间(单位：s)

N1——从事故点到上游路口单向排车队伍可停放的临界车辆数(单位：pcu)

N2——撞车事故发生瞬间撞车点到上游口这段路面正常行驶的车辆数(单位：pcu)

N3——车辆排队队伍中车辆数(单位：pcu)

V——未堵车时车辆匀速行驶的速度(m/s)

CD一设计通行能力(pcu/h)；

C一理论通行能力(pcu/h)；

γ一非机动车影响修正系数；

η一车道宽影响修正系数；

β一交叉口影响修正系数；

n′一车道数修正系数。

2.3 模型建立与求解

目的是要研究横截面实际交通事故所影响的路段车辆跟队长度与事故持续时段、事故实际运力以及路段上游车流量这三个影响因素之间的关系。尝试应用差分算法，把同一时间上游路口流入车辆和事故点处横截面车流出车辆作差，然后求各差值的和，这个量是车辆排队的关键。在某时刻事故发生点至下游路口的总车辆数应等于排队队伍里的车辆数与队伍后面剩下路段正常行驶车辆之和。而这些车辆的积累，源于事故发生瞬间这段路面有的正常的行驶车辆加上在以后的时间里上游路口流入车辆和事故点处横截面车流出车量之差。基于这种思想，可以找出上述各个变量之间的关系。

函数关系如下：

N2+(Q2-Q1)/3600t=N3+L3Q2/(3600V)

(1)

经过分析可得出以下符号量之间的关系：

N1=3L2/(X1+X2)

(2)

N2=Q2L2/(3600V)

(3)

N3=3L1/(X1+X2)

(4)

L3=L2-L1

(5)

因此把式(2)至(5)代入(1)中可得发生交通事故所影响的路段车辆跟队长度与事故持续时段、事故实际运力以及路段上游车流量这三个影响因素之间的关系。

根据二十辆车的平均时速，取V=10m/s

(6)

把X1=4.8m，X2=0.2m，V=10m/s得：

(7)

由此可知，当L1=L2时，t作为一个指标计算结果为：

(8)

可以假设t0为车辆恰好堵满路段，需要处理的时间。

当事故发生时,救急人员务必要在路段恰好堵满之前的t0时间段感到,否则,将会影响上游的车辆通行。若以恰好堵车时刻为零时刻，那么救急人员就要在t-t0时刻之前赶到现场，否则会影响上游车辆通行。

3 问题的进一步分析

交通车流和一般的流体一样，当道路具有瓶颈形式路段，车流发生紊乱拥挤现象，会产生一种与车流方向相反的波，好像声波碰到障碍物时的反射一样，阻止车流前进，降低车速。这种情况在交通流问题中称为回波理论[5]，示意图如下：

图4 交通流回波理论图

其中v1为在A区的车辆的区间平均车速，v2在B区的车辆的区间平均车速。则在时间t内横穿S分界线的车辆数为N=k1((v1-vw)t)=k2((v2-vw)t)，从而

令A B两部分的车流量分别为q1q2，则根据宏观交通流模型Q=kv可得:

(9)

当事故发生时，车辆的初始排队长度为零，当事故持续不疏散时，建立队列长度到达上游路口的时间模型。根据初始材料，事故发生路段各车道宽度为325cm，交叉口间距为48000cm，设计速度为60km/h，交叉口两端均采用信号控制。信号周期为60s，有效绿灯时间为27s(不计绿灯损失时间)，车辆的正常行驶的平均速度为v1=37.35km/h,发生事故后，平均速度下降为v2=9.65km/h，由公式可知，该路段的设计通行能力为：

CD=C·γ·η·β·n′=1730×1×0.875×0.6093×2.60=2399(pcu/h)

由(3-1)所建立的模型可得：

上式的结果说明排队出现了反向的波动，其波动速为83 km/h。由假设跟队的时间为t，初始时段跟队长度记为0，那么在L=140m时，平均排队长度为：

计算得t=12.17s，故经过12.17s后，车辆排队长度达到上游路口。

4 结 论

作为一种方便、直接、便捷的道路停车方式，道路停车其存在具有一定的合理性。然而，利用道路停车进行动态交通将不可避免地导致道路运行能力的下降[6～7]，而由此引发的交通事故也必然会影响到整个路段的交通问题。因此，必须对路上停车事故要严格谨慎处理，对车辆堵塞长度要严格控制，科学的规划和有效率的管理，以及汽车司机认真遵守交通规则的态度和行为，还有道路建设部门对交通道路的设计，使路上在能够满足交通需求的同时，还可以满足一定群众的需要。