基于ABC-BP神经网络的环境敏感监测模型设计研究①

刘 涛

(阜阳职业技术学院，安徽 阜阳 236031)

0 引 言

乔维德将BP神经网络技术应用于翻转课堂的教学评价监控中，改进了BP神经网络模型，使得反转课堂的教学评价模型数据更加客观、真实[1]。赵李明将BP神经网络模型应用于空气质量预测与时空分布的研究中，实现了BP神经网络模型与GIS技术的结合，利用BP神经网络模型监测广州市的空气质量，并提高GIS技术分析的精确性[2]。朱梅实现了BP神经网络算法在等高线生成过程中的应用，利用向量的输入与向量的输出相互对应来建立BP神经网络模型，并利用相对误差检验方式证明了BP神经网络算法在等高线模型生成中应用的可行性[3]。鉴于此，在危险化学气体泄漏的走势监测方面，提出神经网络结合的环境敏感监测模型，目的是提高预测精度，将预测误差率控制到最低。

1 BP神经网算法

短期内风速的变化会对气体的扩散产生直观的影响，但是短期内风速的变化是具有间歇性以及波动性两大特征的，利用BP神经网络建立气体扩散模型可以最大程度上提高气体扩散方向的预测精度。

1.1 BP神经网算法过程

BP神经网络算法利用了梯度下降的基本原理[4]，其算法的目标函数由公式(1)中表示：

(1)

在公式(1)中，ok表示的是在训练样本作用机理的处理下BP神经网络输出节点的输出，yk表示的是与ok同样条件下的目标值，n所表示的是输出的维数，N代表的是训练样本的样本数量。

1.2 BP神经网络的训练步骤

BP神经网络的训练主要可以分为隐含层输出、输出层输出、权值更新、阈值更新、四个部分，这四个部分可以用以下六个公式完成表达[5]。首先对公式中所使用到的字母进行介绍：m-BP神经网络输入层所设置的节点数；n-BP神经网络输出层所设置的节点数；l-BP神经网络隐含层节点数；S-BP神经网络所设置的训练样本数；p-BP神经网络所设置的样本矩阵；b1=n×S-BP神经网络所设置的隐含层阈值；b2=l×S-BP神经网络所设置的输出层阈值；w1=m×n-BP神经网络的连接权值(连接网络输入层与网络隐含层)；w2=l×n- BP神经网络的连接权值(连接网络隐含层与网络输出层)，具体公式如下所示。

隐含层输出：

令n1=w1×p+b1，输出a1=tansig(n1)。其中，tansig(n1) = 2/(1+exp(-2*n1))-1

(1)

输出层输出：

令n2=w2×p+b2，输出a2=purelin(n2)。其中，

purelin(n2)=n2

(2)

权值更新：

w1(t+1)=w1(t)+η[(1-β)D1(t)+βD2(t-1)]

(3)

w2(t+1)=w2(t)+η[(1-β)D2(t)+βD2(t-1)]

(4)

阈值更新：

(5)

b2(t+1)=b2(t)+(yk-ok)

(6)

在完成以上四个部分时，如果误差较大则可以通过不断调整BP神经网络所设置的权值与阈值来调整模型精度。

2 仿真设计

单纯仅用BP神经网络算法架构在危险化学气体泄漏时，对于风速的预测并不是十分精确，为了提高其预测精确度将ABC算法融入至BP神经网络算法，建立起ABC-BP神经网络架构，下面将这一架构进行介绍。

2.1 算法架构模式原理

ABC-BP神经网络架构是在ABC算法原理发展的基础上发展的，在ABC算法原理中，提出了三只蜜蜂的概念，用以帮助人们加深对ABC算法原理的理解。蜜蜂概念中将每一个食物源头设定为算法的一类可行性解，每个食物源头中所包含的食物量设置为这类可行性解的适应范围。采蜜的蜜蜂依据一定的路线选择不同的食物源，并在选定食物源后确定该食物源所拥有的食物量，这可以设定为一个确定适应度的过程。在适应不同适应度的过程中，若新解的适应度比最初算法原理所设置的适应度打，则需要重新选择食物源的位置，最终确定合适的食物源之后，再将这源头的信息传递给观察蜂，观察蜂依据神经网络架构最初设定的最大概率选定新的食物源位置，如果新食物源位置的适应度大于采蜜蜂所确定的食物源位置，则选择新的食物源位置不断重复，直到寻找到最合适的食物源即可停止。

2.2 风速模拟预测

BP神经网络预测的过程中，所确定的训练精度是最重要的一项参数，高训练精度可以建立精度最高的风度预测模型[6]。利用ABC模型与BP神经网络结合所建立的风速模拟预测模型，可以分为初始化食物源、计算适应度值、交叉变异、概率计算四个部分。初始化食物源：设定F个食物源，每一个所设定的食物源代表的参数即为需要优化的权值阈值。计算适应度时需要将所设定的食物源数值代入公式(2)，所得出的结果再代入下面的公式：

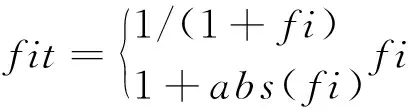
(7)

交叉变异如公式(8)所示：

Vij=xij+φij(xij-xkj)

(8)

概率计算如公式(9)所示：

(9)

在计算概率后得出的结果需要在[0,1]范围内随机选择一个数值进行比较，如果所选择的随机数大于所计算的概率，则需要返回上一步骤，继续进行交叉变异过程。

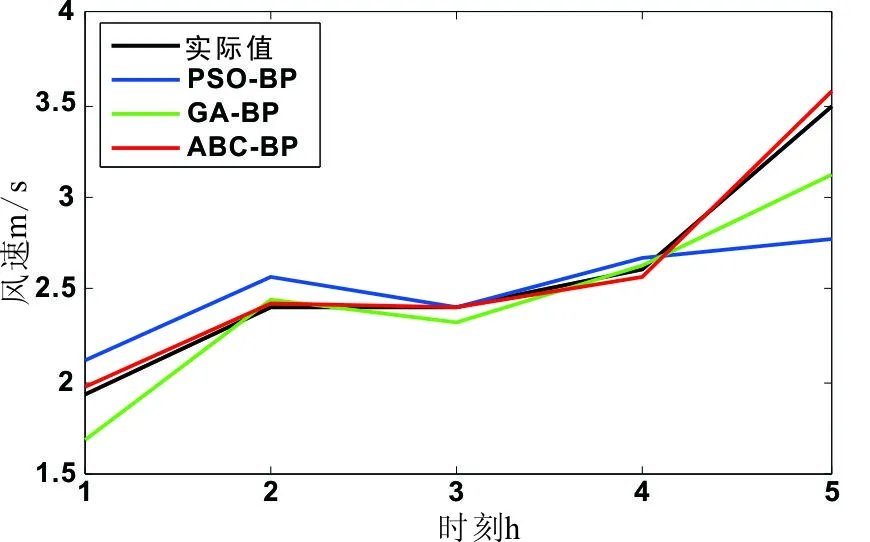
图1 不同算法的预测值与实际值对比曲线图

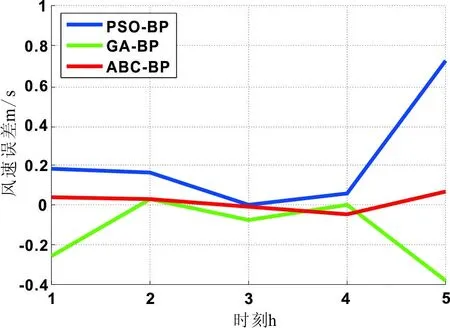
图2 不同算法的预测误差图

3 结果与讨论

经过模型融合后，可以最大程度上降低神经网络的误差值，这个优势是BP神经网络算法与ABC算法优化权值阈值优化之后得到的。在算法设计中假设所设定的食物源数量为100，则在实验过程中所需要迭代10000次才可以完成实验过程，这是指数增长的过程。所设定的食物源数量越多，则得到的误差性能目标值越小，这就不需要进行数据的二次优化。

3.1 实验结果

为了比较各类算法与BP神经网络结合的优缺点，将PSO-BP神经网络、GA-BP神经网络、ABC- BP神经网络进行的预测值与实际数据数值进行对比，所得出的数据图如图1所示，对比不同算法所得出的预测数据的误差数值如下图2所示，所得出的不同算法运算所得出的平均误差如下表1所示。通过图形与数据对比可以看出ABC-BP神经网络算法是最合理的算法。

图1中可以看出，在4h之后，三种算法所得出的预测值的走向发生了明显的变化，其中GA-BP算法以及PSO-BP算法所得出的预测结果与实际值发生了较大程度的偏离，而ABC-BP算法所得出的数值与实际值基本吻合。

由图2可以看出，三种算法所计算出的误差结果差别较大，尤其在4h后的误差走向图完全不同。可以从图2中看出ABC-BP算法所得出的风速误差最小。另外，不同算法的平均预测误差率如表1所示：

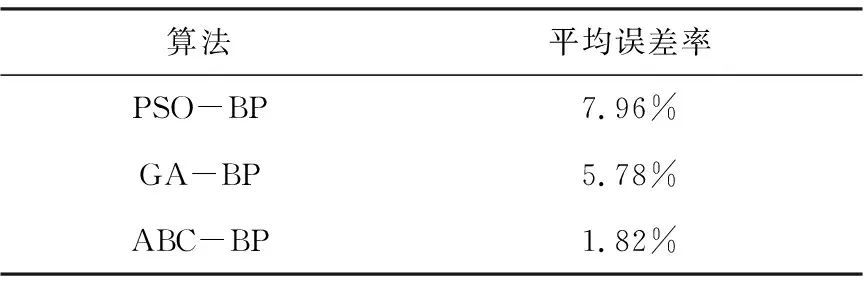
表1 不同算法的平均预测误差率

通过对比可以看出ABC-BP算法的平均误差率最小，控制在2%以内。其他两种算法的误差率已经超过了5%。

3.2 模型可视化应用

基于ABC-BP神经网络模型算法，可以精准的获得气体扩散趋势，既可以获得短期趋势又可以获得长期趋势，并对有毒气体扩散的主方向进行预警。对比网络数据可以得出覆盖面积图示，其中，对比模型预测范围以及实际扩散范围可以计算出危险化学气体的实际扩散趋势。

4 结 论

综上所述，风速以及风力的大小会对危险化学气体的扩散产生影响，短期的风速预测系统可以提前预估有毒气体的扩散范围，提前对周边居民进行预警。传统的BP神经网络预测模型的精度并不十分精确，将ABC算法融入后可以完成对所确立的模型进行校正，最终提高系统的预测精度。