结构损伤识别的截断总体最小二乘法①
2019-02-15王学航杨秋伟白志超
王学航, 杨秋伟, 白志超
(绍兴文理学院土木工程学院, 浙江 绍兴 312000)
0 引 言
近年来,国内外学者对结构损伤识别方法开展了大量的研究[1]。其中,利用结构模态参数的变化来进行损伤识别的方法已成为众多工程领域共同关注的热点。灵敏度分析方法能够直接利用不完备的模态数据来对结构进行损伤识别,受到了广泛研究。
基于灵敏度分析进行损伤识别的方法中,往往是采用最小二乘法对灵敏度方程进行求解。最小二乘法是在残差范数平方和极小的准则约束下求解最佳的相关参数,其仅考虑了测量项引起的误差,然而在构造灵敏度矩阵时仅保留了一阶项而忽略了高阶项,与真正的灵敏度矩阵也存在一定偏差。对此,采用总体最小二乘法在一些其他领域中得到了较好结果[9]。另外,由于测试数据不完备与误差的影响,构建出的灵敏度矩阵往往容易出现病态矩阵而导致识别结果不稳定甚至完全失真。目前已有学者提出岭估计[10]和截断奇异值分解[11]等方法来克服病态方程组问题。相比于岭估计,截断奇异值技术是一种较简单、直接的方法[12]。Fierro等利用广义奇异值分解技术研究了病态总体最小二乘法问题,并提出了截断总体最小二乘法[13]。
基于特征对灵敏度分析,结合截断总体最小二乘法,提出了一种结构损伤识别的截断总体最小二乘法。以一个平面桁架结构为例,对所提方法进行了验证。
1 基本原理
1.1 特征对灵敏度
首先,对特征对灵敏度方法[7]作简单回顾,不失一般性,考虑一个n自由度的结构系统,那么其自由振动的方程为:
Kφi=λiMφii=1,2,…,n
(1 )
其中,K和M分别为系统的刚度矩阵和质量矩阵,φi和λi为第i个振型和特征值。结构发生损伤通常仅引起刚度的变化,结构第i个特征对的一阶灵敏度可以由以下两个方程式计算得到:
(2)
(3)
其中,αj和Kj分别是第j个单元的损伤参数和刚度矩阵,λr和φr为第r个特征值和振型。结构发生损伤后,第i个特征对的变化量可表示为:
Δλi=λdi-λi
(4)
Δφi=φdi-φi
(5)
其中,Δλi和Δφi分别为结构发生损伤前后特征值和振型的变化量,λdi和φdi分别为损伤后第i个特征值和振型。根据泰勒级数展开,Δλi和Δφi的一阶近似值可由以下两个方程式计算得到:
(6)
(7)
其中,N为单元体的总数。若只有m个模态的l个自由度被测量时,一阶灵敏度方程可表示为:
{Δλ}=H1{α}
(8)
{Δφ}=H2{α}
(9)
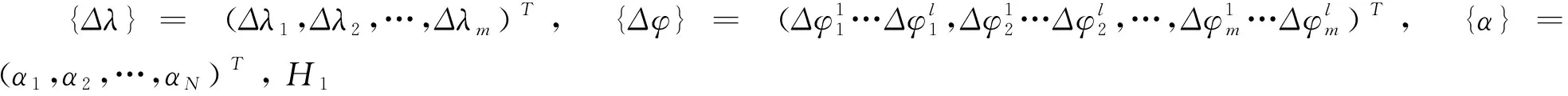
(10)
由线性方程组(10),可以计算出结构的单元损伤参数{α}。
1.2 结构损伤识别的截断总体最小二乘法
对于方程组(10)的求解,通常利用广义逆技术,然后采用最小二乘法计算得出结构的单元损伤参数{α}。但是最小二乘法仅仅考虑了方程组(10)左边测量项的误差,实际注意到方程组(10)中右边的灵敏度矩阵H1和H2仅保留了一阶项而忽略了高阶项,与实际的灵敏度矩阵也存在一定偏差,对于这种情况,在一些其他领域中采用总体最小二乘法得到了较好的结果。将总体最小二乘法应用于损伤识别中,以期取得更加合理的识别结果。
总体最小二乘法的求解是通过奇异值分解技术来实现的。其主要步骤为:首先方程组(10)可改写为:
(11)

Bm(l+1)×(N+1)=
(12)
TLS解可由增广矩阵右奇异向量V的最后一列求得,即结构损伤参数由下式解得:
(13)
由于测量误差和测量的不完整问题,线性方程组(10)往往是病态的,直接采用总体最小二乘法或者最小二乘法得到的结果往往是不合理和不稳定地,许多学者就此也提出了方法。采用截断奇异值技术(TSVD)对病态方程组进行求解,其基本思想是去掉矩阵中的较小奇异值来削弱矩阵的病态。Fierro等[17]对总体最小二乘法做了相关研究,并给出了具体的截断总体最小二乘法解的公式:
(14)
其中,V12和V22由对方程式(12)中的矩阵V分块得到(t表示截断参数):
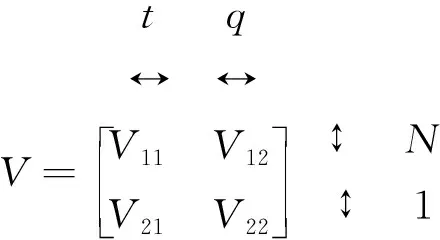
(15)
利用方程(14)可以获得鲁棒性更好的解,这就是本文提出的结构损伤识别的截断总体最小二乘法,在下一章中将通过数值算例来比较这种方法相比于直接使用总体最小二乘法直接求解特征对灵敏度的优越性,讨论在模态参数不完备情况下,测试误差水平的大小对结构损伤识别结果的影响。
2 算 例
以图1所示的平面桁架结构[6]为例来验证上述方法的可行性。该结构的主要参数如下:横截面面积A=0.004m2,杆件长度L=1.52m,弹性模量E=70GPa,密度ρ=2770kg/m2。该结构有限元模型由31个杆件单元、14个节点、25个自由度组成。由于在工程实践中,测试得到的模态参数往往是不完整的且在整个结构中的所有自由度方向上都布置传感器也不经济,因此本例中只考虑前6阶模态,且假设只在节点3、6、7、10、11所对应的10个自由度上布置了测试传感器。
假设单元10刚度损伤15%。为了验证改进后方法的可行性,首先单独使用特征对灵敏度的方法对结构进行损伤识别,分别考虑无误差和5%误差两种测试水平,识别结果如图2、3所示。其中由图2可以看出,当测试无误差时,可以较为准确地判断出单元10发生了损伤;但由图3可以看出,当测试考虑5%误差时,识别结果已经严重失真。因此,在测试模态参数不完备以及测试误差影响的情况下,仅使用特征对灵敏度的方法已经很难对结构损伤状况作出准确判断。
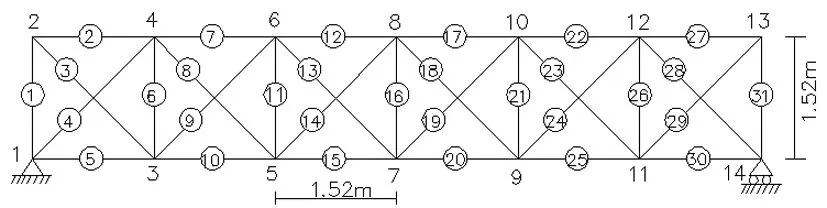
图1 平面桁架结构(31单元)
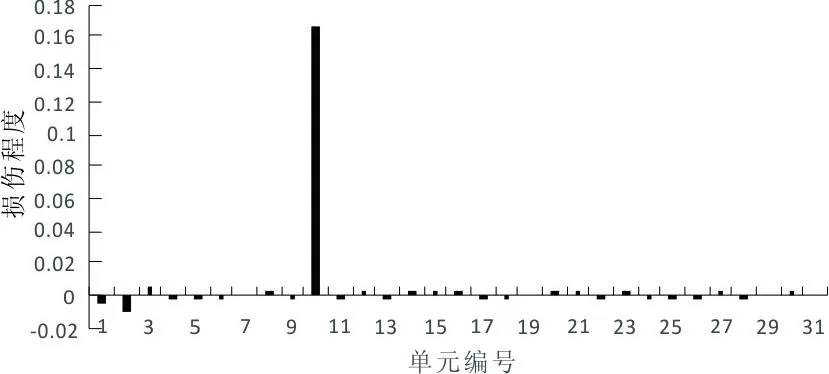
图2 单元10损伤15%时的识别结果(测试无误差)

图3 单元10损伤15%时的识别结果(5%噪声水平)
下面验证所提的改进方法即联合特征对灵敏度与截断总体最小二乘法对结构进行损伤识别的能力。假设两种损伤情况:第一种情况是单元10的刚度损失15%,第二种情况是单元10和单元25的刚度分别损失15%。损伤识别结果如下图4、5所示。其中,每种情况分别讨论三种测试噪声水平,即无噪声、5%噪声、10%噪声。注意,截断总体最小二乘法的公式(15)中截断水平值t取12。
对于第一种损伤情况(单一损伤),由图4可知,在无噪声影响下,通过截断总体最小二乘法可以获得满意的识别结果;当噪声水平为5%时,识别结果仍然良好,可以较为准确地识别出损伤的位置以及程度;当噪声水平为10%时,识别结果虽然会出现误判,但可以明显判断出单元10发生了损伤。
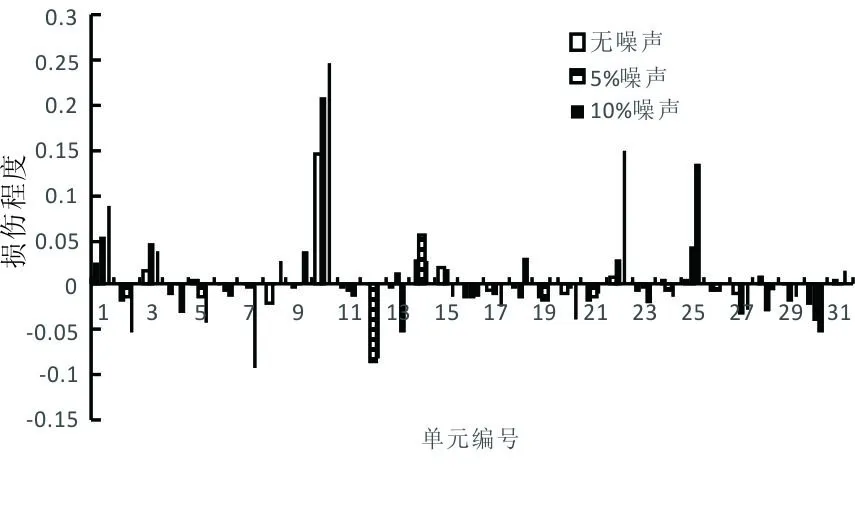
图4 单元10损伤15%时的识别结果

图5 单元10和25同时损伤15%时的识别结果
对于第二种损伤情况(多处损伤),由图5可知,同样在无噪声影响下,通过该方法可以获得满意的识别结果;当噪声水平为5%时,识别结果仍然良好,且精度较好;当噪声水平为10%时,识别结果同第一种情况一样,虽然出现了一些误判,但是可以看到,对于真正发生损伤的单元10和25,其损伤识别程度值明显大于其他值,可以判断出单元10和25发生了损伤。以上结果表明:将截断总体最小二乘法应用于结构损伤识别中,可以获得鲁棒性较好的解。
3 结 论
将特征对灵敏度方法与截断总体最小二乘法结合起来,提出一种结构损伤识别的总体最小二乘法。以一平面桁架结构为例,在测试数据不完备的情况下,详细讨论了误差水平对识别结果的影响。结果表明:所提方法在模态参数不完备的情况下,当数据无噪声时,可以获得比较精确的识别结果;当数据噪声水平较小时,可以获得较为准确的识别结果;当数据噪声水平较大时,仍然可以判断出损伤的部位。所提方法对于测试噪声具有较强的鲁棒性,可供实际工程应用参考。
