有轨电车轻型防爬器结构优化设计

马艳波

(中车长春轨道客车股份有限公司， 130062， 长春//教授级高级工程师)

随着轨道交通的发展，轨道交通车辆轻量化设计逐渐成为车体结构设计中的重要课题之一[1-2]。防爬器作为列车车体端部吸能结构的重要组成部分，其结构形状较为复杂，一般包括防爬齿、缓冲吸能结构及安装板等。在列车碰撞中，防爬齿相互啮合，以防止较大的垂向冲击力导致列车爬车发生，同时将纵向冲击力传递给后端吸能结构，吸收能量。如何在满足结构强度和吸收能量的要求下，减轻结构质量，从而实现防爬器的轻量化设计，是设计的难点。

本文以有轨电车吸能防爬器为研究对象，结合轻型防爬器的强度和动态性能的设计要求，提出了一种防爬器轻量化设计方法。基于Hyperworks软件，引入了拓扑优化的设计思想，以结构材料许用应力和一阶模态为优化条件，对防爬器进行拓扑优化设计，以减轻防爬器的质量，并通过仿真计算和性能试验验证了该方法的可行性。

1 基于OptiStruct的优化方法

1.1 拓扑优化理论

拓扑优化的核心思想是给定设计区域内需求载荷和多载荷结构的最佳材料分配。目前，连续体拓扑优化方法主要有均匀化方法 、变密度法 、渐进结构优化(ESO)法及水平集方法等[3-5]。OptiStruct软件提供了一系列优化工具，其灵敏度分析、尺寸优化和自由尺寸优化等分析方法，能非常有效地辨识出对模态频率和结构强度影响较大的结构部件和结构区域，并且能针对结构部件和区域进行优化设计，最终满足性能要求。此外，该软件带有强大的优化算法，可以用于概念设计和细化设计[6-7]。

1.2 基于OptiStruct的数学模型

优化设计的三要素为设计变量、目标函数和约束条件[8-9]。设计变量是发生改变，从而提高性能的一组参数;目标函数要求最优的设计性能，是关于设计变量的函数；约束条件是对设计的限制，是对设计变量和其它性能的要求[10]。

式中：

X——设计变量，X=(x1,x2,…,xn),在拓扑优化中，设计变量为单元的密度；

f(X)——设计目标函数；

g(X)，h(X)——约束函数。

通过不同类型的信息卡描述。OptiStruct软件采用数学规划方法，通过求解灵敏度构造近似显示模型，采用小步长迭代找到最优解。具体优化流程如图1所示。

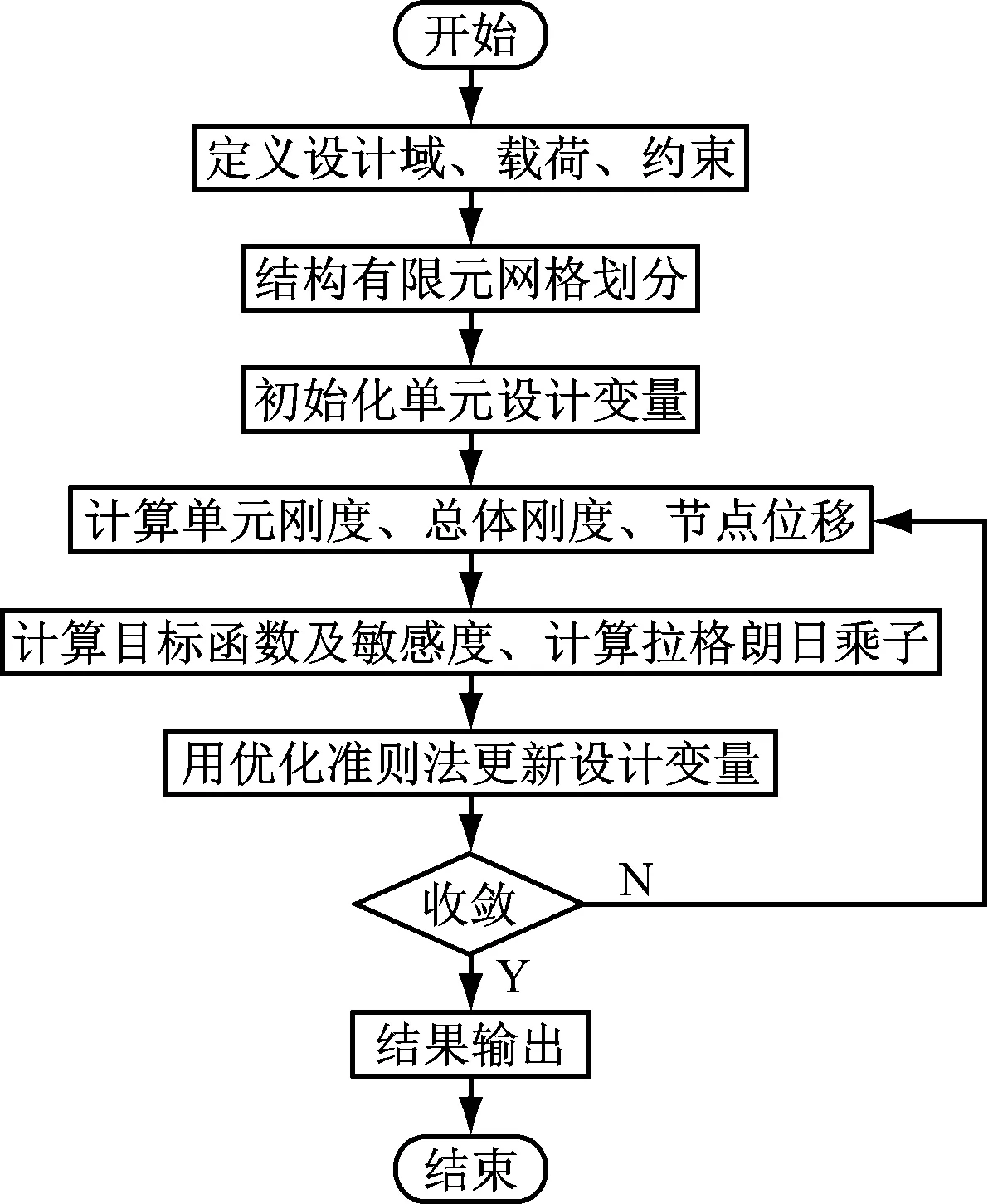
图1 基于变密度法的拓扑优化流程图

2 防爬器结构设计拓扑优化设计

2.1 建立拓扑优化模型

在进行拓扑优化时，要根据实际结构形状，采用实体单元建立初始拓扑优化的模型，定义结构中的优化区域和非优化区域。对于防爬器结构，既要减轻其质量，又要不影响其吸能效果。可将防爬齿设定为优化区域，将吸能结构设定为非优化区。本文采用四面体单元对防爬齿进行网格划分，利用拓扑优化将优化区域中多余材料删除。防爬齿拓扑优化模型如图2所示。

图2 防爬齿拓扑优化有限元模型

2.2 模型载荷、约束条件及目标函数

拓扑优化计算考虑了防爬器在不同车速下的冲击载荷。结合设计要求，确定了防爬齿结构设计载荷，并将其作为拓扑优化的纵向载荷。由于防爬齿和吸能管刚性连接，因此，将吸能管与防爬齿接触端面的自由度全约束。防爬齿整体结构刚度和动态性能的要求为：在纵向加载作用下，保证材料最大应力小于许用应力，一阶模态频率大于路基激励频率。优化设计要在满足上述要求时，使体积分数最小。优化设计变量为设计空间里每个单元的密度，计算收敛的公差为0.005。

2.3 拓扑优化结果

拓扑优化采用OptiStruct进行求解。每次迭代计算用时约1 s，经过120次迭代计算后，防爬齿模型趋于稳定状态。此时，认为计算收敛得到1个最终的拓扑优化结构模型。拓扑优化利用单元的密度值(0～1)来表示优化后材料分布(颜色较浅区域即为密度值较小，此区域材料被去除)。优化最终结果如图3所示。体积分数收敛情况如图4。

图3 拓扑优化结果

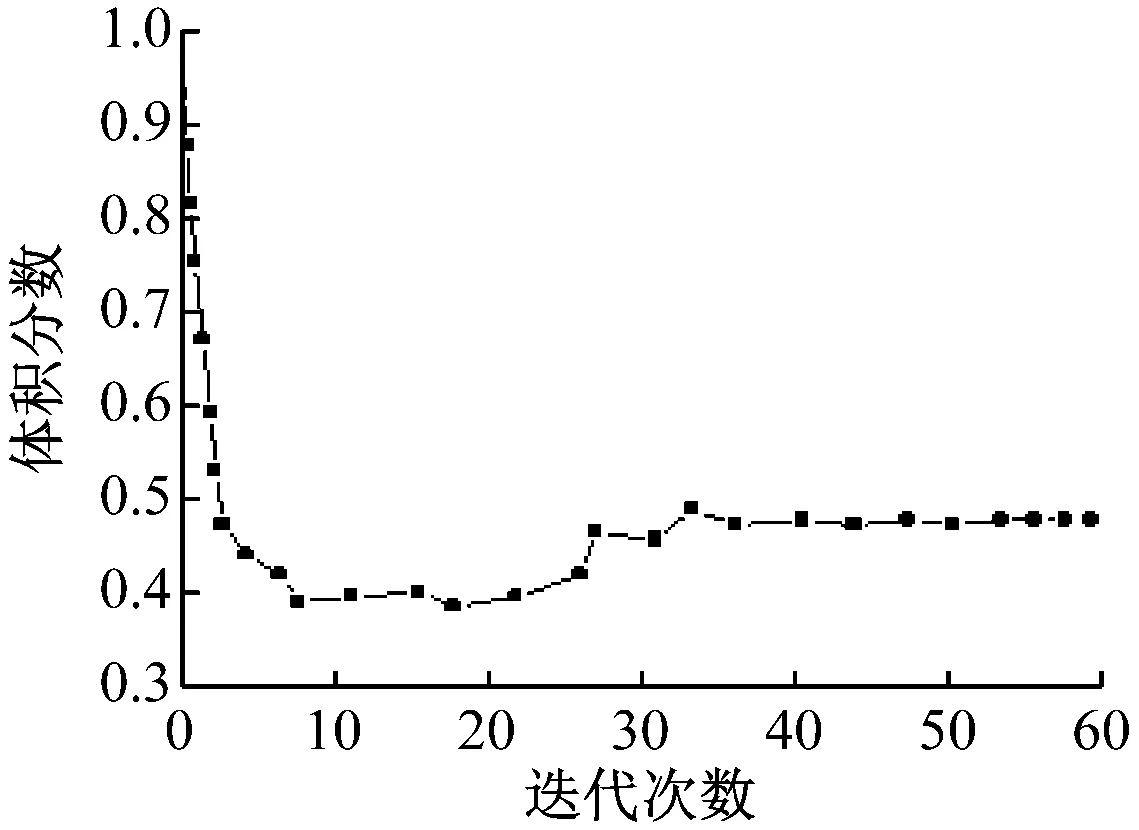
图4 拓扑优化体积分数收敛情况

3 防爬器结构精细化设计

防爬齿拓扑优化结构是个概念性的结构模型，表征了防爬齿主要的承载结构的位置和形状，为防爬齿的结构设计提供了重要参考。但其并不能描述防爬齿的详细参数，因此，需要结合具体的制造方法和工艺，对防爬齿进行精细化设计。防爬齿精细化结构如图5所示。根据防爬器的吸能要求，设计吸能器，并构成完整的轻型防爬器(如图6所示)。图7为目前常用的典型防爬器结构。

图5 防爬齿精细化设计

图6 轻型防爬器结构

图7 常用典型防爬器结构

4 防爬器结构性能验证

基于结构轻量化的要求，防爬齿材料选择铝合金材料6061-T6。其抗拉强度为310 MPa，屈服强度为255 MPa，弹性模量为69 000 MPa，密度为2 700 kg/m3，泊松比为0.33。对防爬齿结构进行了仿真计算，得到结构在静态作用下的应力分布情况，并进行了准静态压缩试验。图8为防爬齿有限元模型。

图8 防爬齿有限元模型

图9为防爬齿应力云图。由图9可知，防爬齿表面最大应力为250.9 MPa,小于材料的屈服强度255 MPa，最大应力出现在防爬齿固定约束位置，此处出现较大的应力集中，与实际情况一致。

对防爬齿进行静压试验。静压试验示意图见图10，静压试验结果见图11。由图11可知：防爬齿在承受550 kN的纵向压力时，未出现塑形变形；当卸载结束时，防爬齿未出现残余位移，满足强度要求。

图9 防爬齿应力云图

图10 防爬齿静压试验示意图

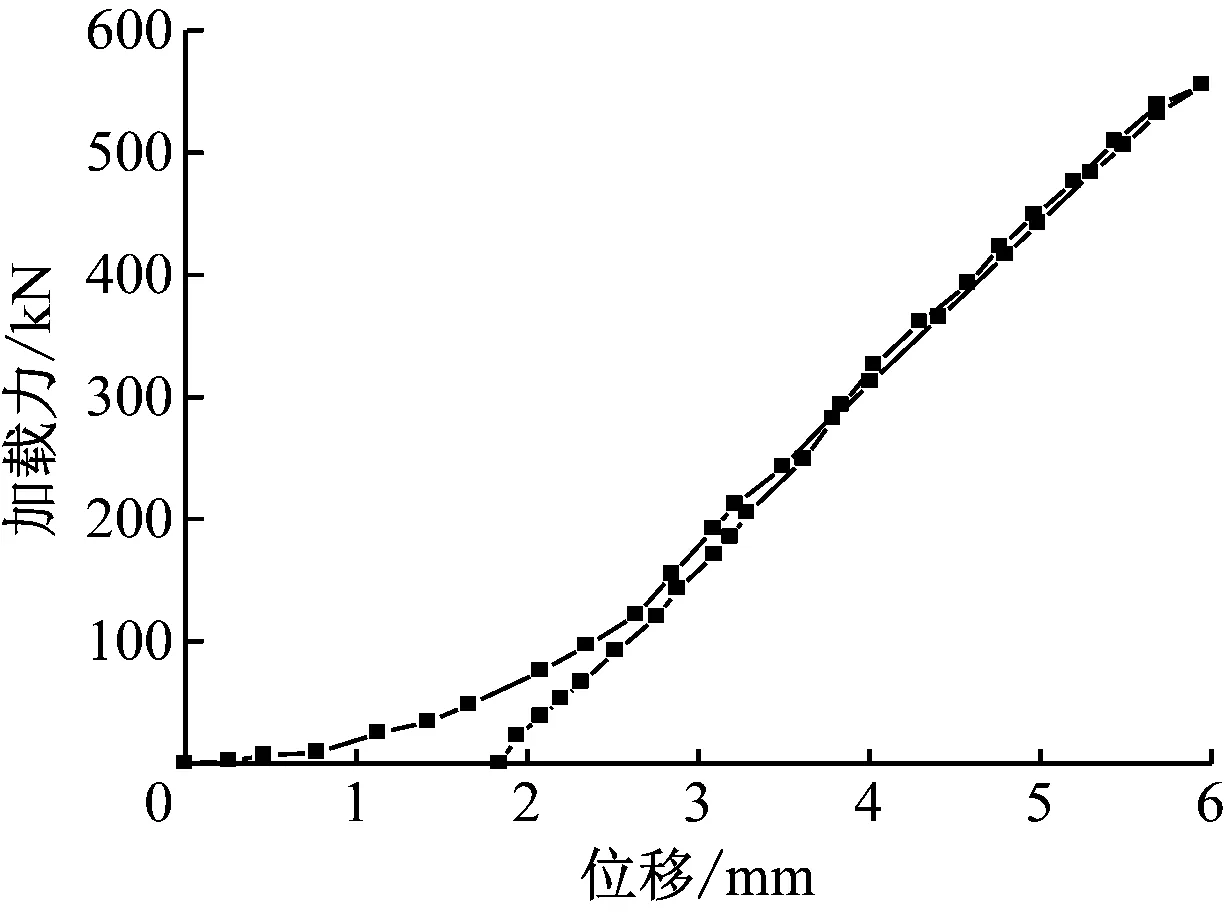
图11 防爬齿加载力位移曲线

列车碰撞过程中，防爬器的低阶模态频率对车端结构动态特性影响较大。列车行驶的激励频率大都在30 Hz以下。根据设计要求应控制防爬器的一阶模态值高于30 Hz。

对优化后防爬器进行了自由模态分析，其结构模态振型如图12所示。提取防爬器前六阶模态频率，如表1所示。从模态分析结果可知，结构一阶模态为53.32 Hz，有效地避开了列车行驶振动频率敏感范围。

表1 优化后防爬齿模态频率

a) 第一阶模态振型

b) 第二阶模态振型

c) 第三阶模态振型

d) 第四阶模态振型

e) 第五阶模态振型

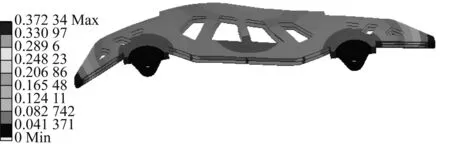
f) 第六阶模态振型

拓扑优化的结果见表2。由表2可知，拓扑优化在满足强度设计要求的同时，可降低结构质量10.24%。

表2 防爬齿优化结果

5 结论

(1) 在假定的防爬器设计空间内，通过静态拓扑优化方法得到了在满足强度和动态特性要求下最小车体质量的材料分布，根据拓扑优化概念模型，设计出了满足强度和轻量化要求的防爬齿结构。

(2) 优化前防爬齿的最大应力为264.3 MPa，优化后最大应力为254.6 MPa。在防爬齿运动约束位置出现应力集中，但均低于材料的屈服强度(255 MPa)，符合强度要求。

(3) 优化后的防爬齿一阶模态频率避开了列车行驶振动频率敏感范围，提高了设计质量。

(4) 拓扑优化重新分布材料后，使防爬齿总体质量减轻了10.24%，从而节约了生产成本。

(5)拓扑优化可以在保证结构性能、满足要求的前提下，使材料得到最优的分布，减轻了结构质量，为今后防爬齿的设计提供参考。