改进的基于排序的DDM算法

张霞,延耀威

(山西大学 计算机与信息技术学院,山西 太原 030006)

0 引言

HLA是用来构建大型复杂仿真系统的新型的分布式仿真技术,该技术通过仿真运行平台将多个分布在不同地理位置的联邦成员关联起构成复杂的仿真系统支持联邦成员之间的交互,可以实现仿真成员的即插即用,满足分布式仿真系统要求的可扩缩性和可重用性[1]。HLA 的运行支撑环境将复杂的上层仿真系统与底层通信系统分离,它由联邦/联邦成员规则、对象模型模版、接口规范、运行支撑环境等组成[2-3]。其中运行支撑环境接口规范包含联邦管理、时间管理、声明管理、所有权管理、对象管理和数据分发管理[4-5]6个方面的内容。

1 DDM算法概述

DDM是HLA的重要管理服务之一,是支撑运行环境在声明管理服务实现基于类的数据过滤后,再对区域发布的数据值进行过滤,其目的是为了减少在大规模分布式仿真中大量不必要数据和冗余数据的发送与接收。DDM算法的关键是判断仿真成员发布区域和订购区域是否存在交叠区域,如存在,则发布邦员将发布数据发送给指定的订购邦员。在大规模的仿真实验中,仿真实体之间的交互数据量非常庞大,这会占据大量的网络资源,所以管理仿真实体之间的数据流量交互,减少冗余数据的分发,对于解决网络资源拥堵,降低仿真延迟,增强仿真的可扩缩性具有重大的意义。

DDM数据分发管理算法的本质是判断存在重叠的发布区域和订购区域,确定发布者和订购者之间的供求关系,其匹配算法的时空复杂度直接决定着分布式仿真系统的稳定性和可扩缩性。经典区域匹配算法有直接区域匹配算法、基于排序算法、基于网格算法[6-7]。

直接区域匹配算法是在定义好的路径空间上建立多维坐标系统,在相交区域匹配过程中,通过遍历每一个发布区域与所有的订购区域进行区域匹配,若发布区域与订购区域有相交区域,则认为仿真实体之间存在数据交互,为精确匹配。但是随着仿真复杂度的不断扩大,实现直接区域匹配算法时需要的区域匹配的计算量也将会十分庞大,耗时会呈指数级增长。若有n个订购邦员与n个发布邦员进行仿真实验,则所需的匹配时间为0(n2),算法的可扩缩性差。

基于网格的方法提供了一种间接的区域匹配方法,多维路径空间被分割成为边长大小相同的网格,若订购区域与发布区域覆盖了相同的网格,则认为相应的仿真实体之间存在数据交互,以此确定哪些仿真实体之间是有数据交互,避免发送冗余数据。基于网格的方法易于实现,且具有较好的可扩缩性,但是,存在发布区域与订购区域覆盖同一个网格但没有交集的情况,即虚假连接;若发布区域与订购区域同时覆盖了多个相同的网格,数据会重复发送,即存在冗余连接[8-12]。基于网格算法的匹配时间与网格的密度有很大关系,网格密度越大,匹配精确度越高,但匹配时间越长,虚假连接少;网格密度越小,匹配精度越低,虚假连接多。

基于排序的算法是将发布区域和订购区域的高低坐标值投影在路径空间的坐标系统上,若发布区域高低坐标范围和订购区域的高低坐标范围在路径空间上所有维度都有重叠,则认为发布区域和订购区域相交,算法是精确匹配。假设在d维路径空间上共有n个订购区域与n个发布区域进行仿真实验,则所需的匹配时间为O(d×nlogn)。因而,在大规模仿真中区域匹配算法依然具有较好的扩充性和健壮性。但是,基于排序的DDM算法[13-17]在进行匹配的过程中,要判断每一个边界值的信息,包括该边界值是订购区域还是发布区域、上边界还是下边界,并且需要消耗存储空间将扫描到的边界值存储在集合中,算法的时空开销大。

2 改进的DDM排序算法

在原始的排序算法中,每一维的交互信息都需要一个对应的矩阵来存储,即需要大量的存储空间,而且需要大量时间对边界类型进行判断,而改进的排序算法在映射基础上,将发布区域与订购区域的边界值分开存储并排序,并通过判断订购区域中的边界值是否处于发布区域上下边界值的区间内,如果处于区间内,则订购区域与发布区域相交。

初始时,将区域的各维信息分别存储在各自对应的集合中,并将发布区域与订购区域的边界信息分开存储。然后,将订购区域的边界信息集合进行排序,通过遍历发布区域,与所有订购区域依次进行匹配,假设发布区域与订购区域数量相等且都为n,那么将区域的重叠信息记录在一个初始化为0的n×n的矩阵中,它的行列号分别代表订购区域与发布区域。在对当前维度上的相交信息存储时,只需对存储矩阵中与之前匹配过的维数相等的元素值所对应的区域信息进行处理,如果当前维度有重叠则将矩阵中对应的元素加1。对路径空间中的所有维度重复上述步骤,如果最后矩阵中的元素值与维数相等,则认为该元素值对应的发布区域和订购区域就有交叠。

图1是一个二维路径空间的示意图,路径空间中有两个联邦成员F1={(P1),(S1)},F2={(P2),(S2)}。由图可知,将发布区域在X轴上的高低坐标值表示为(XSi,X1Si)在Y轴上的高低坐标值表示为(YSi,Y1Si)。

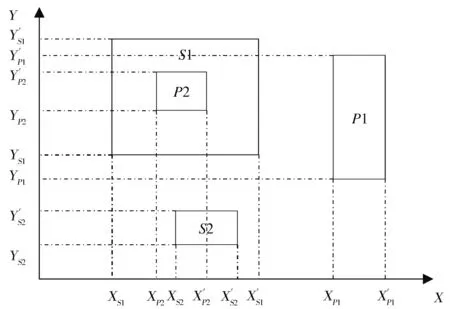
Fig.1 Two-dimension spatial schematic diagram图1 二维空间示意图

改进后的排序算法实现过程如下:

(1)在X维、Y维插入集合时,把订购区域与发布区域分开存储:

X维订购区域:{XS1，X’S1，XS2，X’S2}

X维发布区域:{XP1，X’P1，XP2，X’P2}

Y维订购区域:{YS1，Y’S1，YS2，Y’S2}}

Y维发布区域:{YP1，Y’P1，YP2，Y’P2}

(2)将X维、Y维订购区域的坐标点按值的大小由小到大分开排序

X维:{XS1，XS2，X’S2，X’S1}

Y维:{YS2，Y’S2，YS1，Y’S1}

同时为存储交叉信息建立一个2*2矩阵,矩阵的行列数与发布区域和订购区域相同,分别用来存储各维相交信息的结果,矩阵初始化为0。

(3)首先对X维进行处理,将发布区域集合中的值,依次与订购区域中的值进行比较。

1>XP2:P2的低边界点,将XP2与订购区域中的值比较,若XP2的值大于订购区域的边界值,即XP2>XS1,则将P2的高边界点X’P2从XS1开始与订购区域中的值依次相比较,若X’P2的值大于订购区域中的边界值,即X’P2>X’S2,则停止比较。

2>则在1>中与发布区域上下边界都比较过的订购区域,就认为与该发布区域在X维上有交集。

3>将发布区域集合中所有的边界点都做该比较。获得X维的矩阵相交信息为:

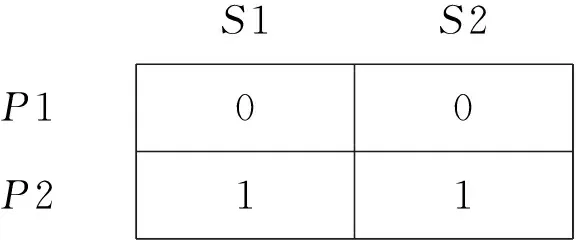
S1S2P1P20011

(4)同理,将Y维中的边界信息也进行如步骤(2)中的匹配,得到的相交矩阵信息为

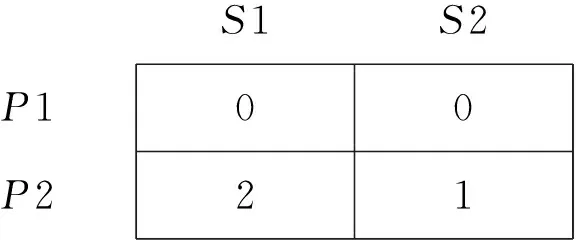
S1S2P1P20021

这种改进的基于排序的DDM算法是利用高低边界值投影在坐标轴上,然后根据值的大小所覆盖范围的相交信息判定各区域之间的匹配关系。算法将各维度的订购区域的上下边界值分开存储进行排序,然后利用发布区域的边界值信息扫描订购区域的有序表,并进行比较,在存储矩阵中填入相交信息。在后续维度的匹配中,相交信息只需要对该矩阵中的元素值进行修改,有交叠区域则将对应的值加1,降低了算法的空间复杂度,而且在匹配坐标值过程中减少了判断次数,从而减少了匹配时间。

3 仿真实验数据分析

本文参考了相关文献设计了仿真实验[18],用计算机模拟随机产生数量不同的仿真区域,通过DDM算法判断发布区域与订购区域之间是否存在交叠区域,仿真平台为Windows7旗舰版64位系统,运行内存为2GB,CPU为单核3.0 GHz。在空间路径坐标系中随机产生1 000,2 000,3 000,4 000,…,9 000个大小不同的矩形区域,每个联邦成员中包含的区域的数目分别选用1,10,2,则仿真节点数量的范围是从1 000到9 000之间变化,限域边长采用10,150,200。由于不同限域的实验结果差别较小且类似,所以图2(a),图2(b),图2(c)分别给出在路径空间为二维、三维、四维情况下,限域边长选择150时所产生的实验结果。

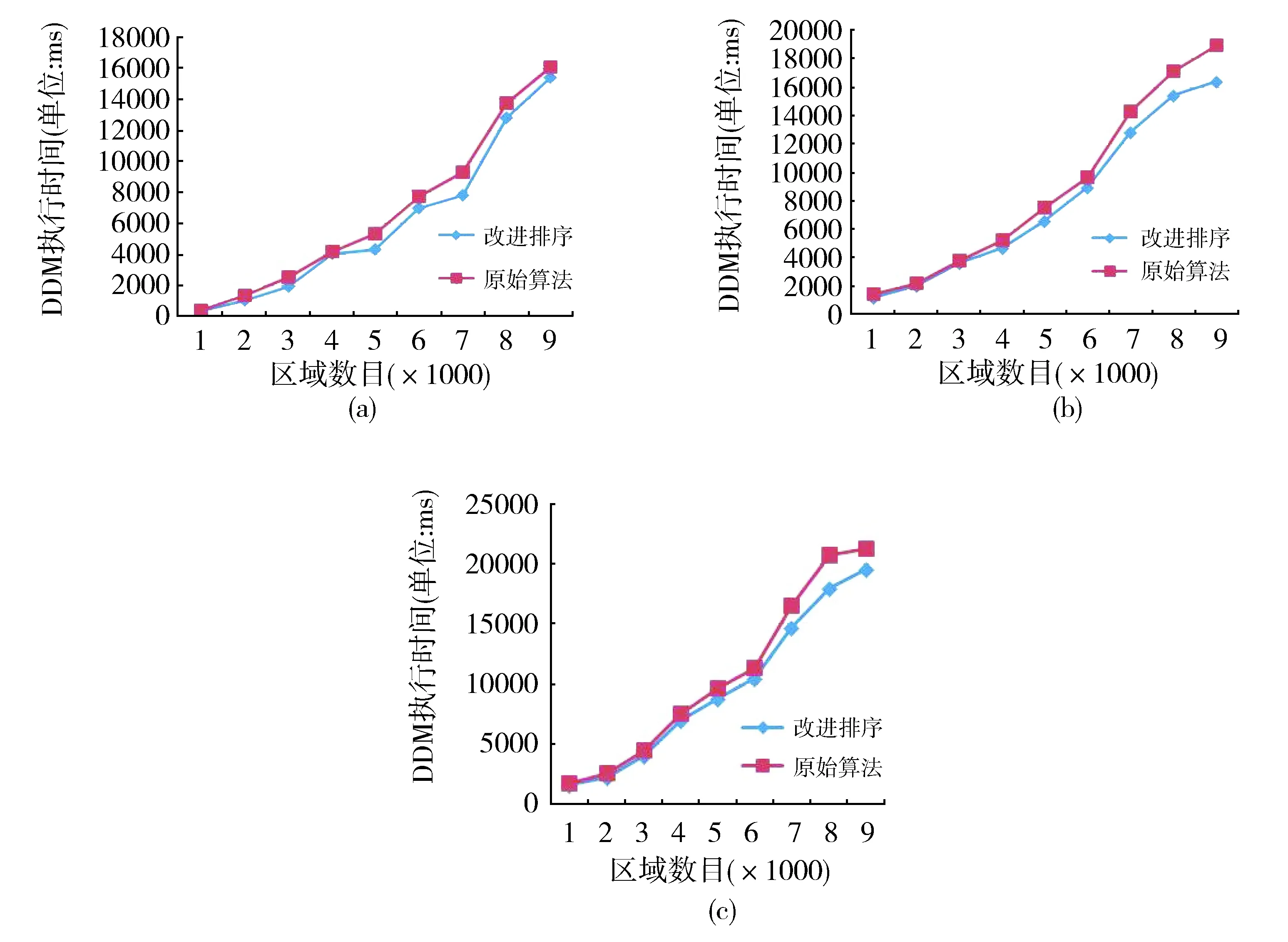
Fig.2 Comparison of execution time in 2-dimension,3-dimension and 4-dimension图2 执行时间在二维、三维、四维下的比较

由实验结果图可以看出,改进的排序算法在仿真规模较小,区域数目较少(少于4 000)时,算法的时间执行效率并没有明显优于经典的排序算法;而随着仿真规模的不断扩大,区域数目大于4 000且不断增大时,改进算法的与经典算法时间执行效率的差别逐渐显现。而且,仿真的系统维度越多越复杂,改进算法在时间执行效率上越优于经典算法。

从以上分析可以得出,随着仿真节点以及区域数目的增加,改进算法的执行时间与空间都优于原始算法,算法在仿真交互数据达到一定数量时,算法执行时间提高比例稳定在9%左右。

4 结论

本文在区域映射到路径空间的基础上,将发布区域与订购区域的上下边界值分开存储,并通过判断订购区域中的边界值是否处于发布区域上下边界值的区间内来确定是否相交,提高区域匹配的运行效率;并通过只对一个存储相交信息矩阵的修改,降低了算法空间复杂度。在仿真实验中考察了算法在区域数目、限域数目、联邦数目情况下的平均匹配时间,实验结果表明改进算法在时间效率和空间效率上都具有优势,随着区域数目的不断增加,在仿真数据达到一定规模时,改进的排序算法执行时间提高比例稳定在9%,对大规模仿真系统的可扩缩性有很好的支持。