例谈“一题一课”与高三复习教学*
——以解三角形为例
2019-02-15
●
(回浦中学,浙江 临海 317000)
根据统计,三角函数每年考查的题量和分值都较为稳定,一般为一个大题加一两个小题,分值在20分左右,而解三角形是其中必考的一个知识点.在考查知识点的同时也考查了数形结合、转化化归、函数与方程等数学思想方法.复习时,如果我们能细心揣摩用好高考真题,一方面可以减轻学生的课业负担和节约教育成本[1],另一方面对学生理解和巩固知识以及训练和培养解题能力都具有一定的帮助[2].

图1
1 真题呈现

(2018年浙江省数学高考试题第13题)
学生基本上能很快作出解答,在△ABC中,由正弦定理得
即
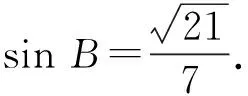
在△ABC中,由余弦定理得
a2=b2+c2-2bccosA,
即
解得c=3或c=-1(舍去).
熟练应用正弦定理和余弦定理是解题的关键,在学生独立完成该题后思考:
思考1以上考题考了哪些知识点?请一一列举出具体内容.
思考2三角形6个元素,知道其中几个元素,求另外几个元素,还有哪些类型?一般可用什么定理求解?

2 变式探究
探究1改变真题的所求.

1)求△ABC的面积;
2)判断该三角形的形状(锐角三角形、直角三
角形、钝角三角形);
3)求边BC上的中线长.

设计意图本变式改变了真题的所求.通过本题的解答,让学生进一步体会解三角形中相应知识点的应用,为后面的变式作好铺垫.
探究2改变真题的条件.

思路1(边化角) 利用正弦定理得
2cosA(sinCcosB+sinBcosC)=sinA,
即
2cosAsin(B+C)=sinA,
从而
2cosAsinA=sinA,
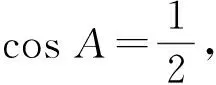
思路2(角化边) 利用余弦定理得
即
b2+c2-a2=bc,
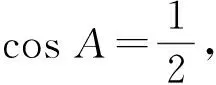
思路3(向量投影) 其实ccosB+bcosC是向量投影概念的应用,即
ccosB+bcosC=a,
从而
2cosA·a=a,
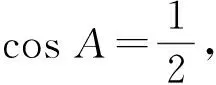
设计意图变式2是让学生体会如何根据已知条件实现边角的灵活转化.对一道题而言,是选择“边化角”还是“角化边”,不可以一概而论,有时两者皆可,有时只能一种才可解决.在该环节中,还可以继续改变a的取值,进而求三角形解的个数.
探究3改变真题的条件或所求.

思路探求利用方程思想得到方程组
利用整体思想可求出b+c=5.

思路1(边) 由余弦定理得
a2=b2+c2-2bccosA,
即
7=b2+c2-bc,
利用基本不等式可得
从而
又由三角形两边之和大于第三边可得

思路2(角) 由正弦定理得
即


思路3(形) 如图2,点N为BC的中垂线与△ABC外接圆的交点,以B,C为焦点、点N到BC的距离为短半轴长画一个椭圆,BA的延长线交椭圆于点M,联结MC.当点A运动时,
当此类题目出现在选择、填空题时,从形的角度可以很快解决.

思路1(边) 因为
7=b2+c2-bc≥2bc-bc=bc,
所以
0 思路2(角)bc= 2RsinB×2RsinC= 图3 思路1(边) 由7=b2+c2-bc可知 b2+c2=7+bc, 又由变式3可知 0 进而得到b2+c2的取值范围是(7,14]. 思路2(角) 由7=b2+c2-bc可知 b2+c2=7+bc, 又由变式3可知 从而 图4 思路3(形) 如图4,D为BC中点,当点A在运动时,因为|AD|≤|AO|+|OD|,所以当点A运动到点N时,中线AD最长.由平行四边形对角线的平方和等于各边的平方和可知 (2AD)2+a2=2(b2+c2). 变式4~6都可以从“边”“角”“形”这3个角度解决.但是若将△ABC改为锐角三角形,从边的角度思考就不好控制了,此时只要化成角B的三角函数,再确定好角B的取值范围即可求出函数的值域.当然若是出现在选择、填空题时,从形的角度出发,结合临界位置就能很快求得取值范围. (2011年全国数学高考理科试题第16题) (2014年全国数学高考卷Ⅰ理科试题第16题) 通过这节课的复习,学生们收获比较大,从多个角度思考问题,感受到了数形结合、转化化归、函数与方程等数学思想方法的渗透.我们在求解过程中也发现:从“边”的角度思考有时问题解决很轻松,但是不具备通用性,而从“角”的思路出发,虽然有时解题比较繁琐,用到了三角恒等变换中的变角、降幂、辅助角公式等,但是具有通用性.因此在“一题多解”时,一方面让学生理解触发各种不同解法的出发点,另一方面是让他们体会一题多解,更重要的是学会判断、甄别在这些方法中哪些方法是最优的、为什么最优.通过这样的环节,学生形成优化的解题思路,既能通过一题多解锻炼思维,又能迅速找到最优解法.
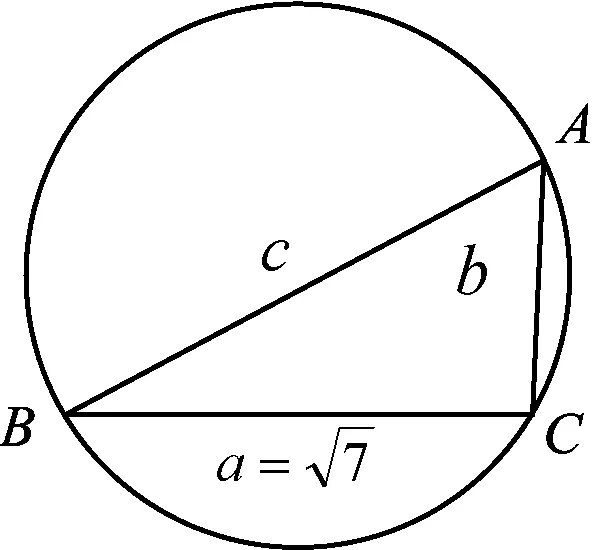







3 高考链接


4 反思感悟
