基于KPCA和SVM的工艺管道腐蚀速率预测
2019-02-14,,,
,,,
(北京化工大学 化工安全教育部工程研究中心,北京 100029)
工艺管道中影响腐蚀的因素众多,腐蚀速率与管道内的介质成分、环境条件以及管道运行时间等息息相关[1]。一般情况下,腐蚀影响因素之间相互关联,这使得管道内的腐蚀情况十分复杂。此外,管道内影响腐蚀的诸多因素也是不断发生变化的,这导致难以用函数表达式直接建立起影响因素与腐蚀速率之间的关系。
目前,国内学者就管道腐蚀速率预测问题,进行了大量研究。喻西崇等[2]在灰色模型的基础上进行了改进,实现了管道腐蚀速率趋势预测;张镇等[3]将灰色理论与人工神经网络、时间序列分析方法相结合,建立了灰色组合模型来预测管道腐蚀速率;王海涛等[4]采用三次指数平滑法,对已有的腐蚀速率统计数据进行拟合,并对腐蚀速率进行了预测分析。现有研究中的预测方法各有特点并且都能够对管道腐蚀速率进行预测,但这些方法多从单一角度进行分析,未能全面考虑管道腐蚀影响因素及其相关性和冗余性,这不可避免造成了预测误差;另一方面,用于腐蚀速率预测的样本数据有限,因而预测准确性也在一定程度上受到了制约。
因此,为解决有限样本数据条件下工艺管道中腐蚀速率难以估算的问题,本工作采用核主成分分析方法对多种腐蚀影响因素进行融合处理,摒弃核主成分分析结果中贡献率低的主元变量,将贡献率高即包含主要信息的主元变量作为输入,腐蚀速率作为目标输出,建立支持向量机模型来对管道腐蚀速率进行预测。
1 核主成分分析
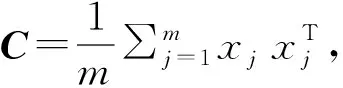
核主成分分析(KPCA)是PCA算法的改进,它采用非线性方法来提取主成分[5]。KPCA首先对样本xk进行非线性变换φ(xk),将其映射到高维特征空间F,此时协方差矩阵为
上述矩阵的特征值λ和特征向量V满足以下条件
λV-CV=0(2)
引入非线性函数φ(xk),可得
λφ(xk)V-φ(xk)CV=0(3)
上式中的特征向量V可由φ(xi)线性表示,即
将式(2)和式(4)代入式(3),并引入核函数Kij=K(xi,xj)=φ(xi)φ(xj),简化后有
mλα-Kα=0(5)
式中:α为核矩阵K的特征向量。对于任意样本,在特征空间F中主元φ(x)上的投影为

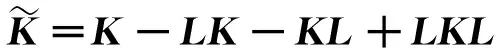
式中:L为m×m阶单位矩阵,系数为1/m。
2 支持向量机
支持向量机(SVM)是一种以统计学习理论为基础,专门处理小样本情况下非线性分类和回归问题的新颖算法[7],最早由Cortes和Vapnik于1995年提出。在处理回归问题时,其基本思想是通过一个非线性映射将低维空间非线性回归问题转换到一个高维特征空间(Hilbert空间),然后用数据集在此高维特征空间中建立模型来进行回归拟合[8-10]。
本工作选取工艺管道中腐蚀影响因素原始数据经KPCA融合后累计贡献率在85%以上的主元变量作为模型输入,腐蚀速率为输出,建立了一个如图1所示的支持向量机模型,该模型为多输入单数输出结构。
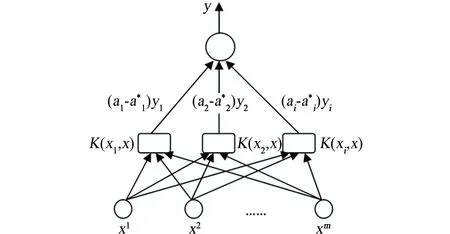
图1 支持向量机模型结构Fig. 1 Support vector machine model
利用支持向量机的基本思想,将数据集(x1,x2,…,xm)通过非线性映射φ(x),映射到一个高维的特征空间,然后用数据集X在该空间建立模型来进行线性回归,回归函数形式如下:
f(xi)=ω·φ(xi)+b(8)
式中:ω,b是回归因子,为模型中待确定参数。
为求得回归函数,将上述问题转换为下列规划问题:
约束条件为:
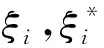
通过引入拉格朗日函数,将上述的优化问题转化为Lagrange对偶问题,求解得

将式(11) 代入式(10) 中,可得下式
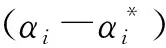
3 验证及分析
本工作数据源于四川石化某装置三条精制柴油管道,各管道腐蚀影响因素值及实测腐蚀速率分别见表1。表中腐蚀速率由电阻探针在线监测得到,部分影响因素数据是经采样分析计算得出的,压力和温度由现场监测仪表得到。
由表1可见:对于上述三条管道,均选取的影响管道内腐蚀速率的主要因素有测试时间、压力、温度、总硫含量、氮含量、pH、氧含量、流速等8个。其中,构成原始数据集的共3个数据集,每个数据集包含24组样本。选取管道a的24组样本数据作为训练样本,管道b和c的样本数据作为测试样本。
3.1 KPCA中核参数σ的影响
核主成分分析中最关键的是核参数σ的确定,目前仍无统一的选择标准。为研究不同核参数对最终预测误差的影响,将KPCA核参数σ作为单一变量,选用不同的参数值对样本进行核主成分分析,建立SVM模型来预测腐蚀速率,并根据式(13)计算预测结果的平均相对误差。图2和表2分别为核参数与误差的关系曲线图及相应的计算数据。
由图2可知,预测误差emape随着核参数σ值的增大先减小后增大至不变,当σ=100时,emape最小。
3.2 KPCA结果及分析
利用KPCA对训练样本进行处理,提取贡献率较大的前8个特征值和相对应的贡献率,各特征值的对应贡献率如图3所示,根据各特征值的贡献率计算累计贡献率,结果如表3所示。
由表3可见:前3个特征值的累计贡献率已达到85%,故选取前三个特征值所对应的主元作为支持向量机模型的输入,建立支持向量机模型。对比原始样本发现,KPCA方法在最大程度保留原始样本信息的情况下,实现了样本维数的缩减,将样本维数由原来的8维缩减到3维,降低了影响因素间的冗余性,为建立SVM预测模型奠定了基础。
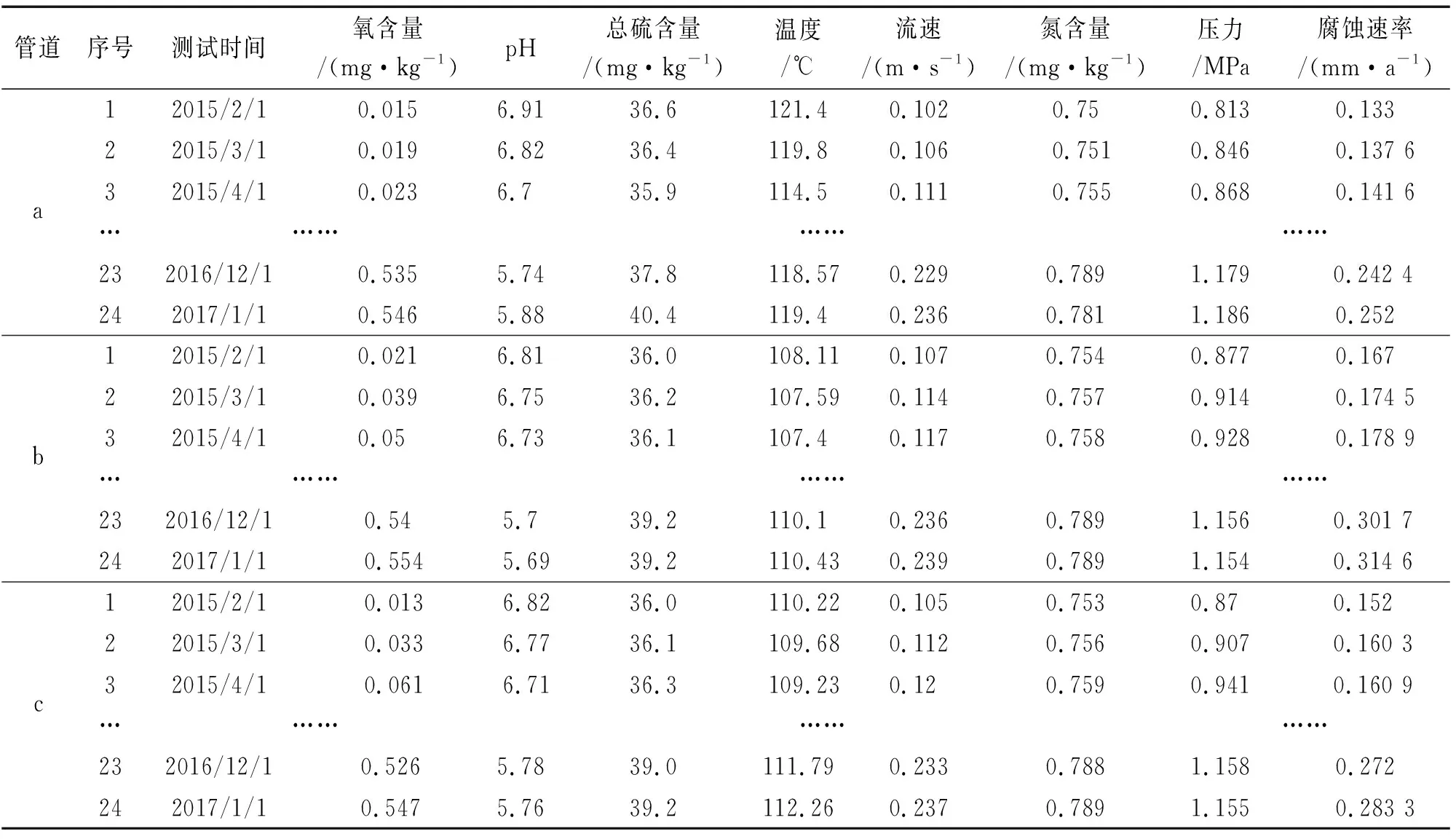
表1 三条管道的腐蚀影响因素及对应腐蚀速率Tab. 1 Corrosion influencing factors and corresponding corrosion rates of three pipes

图2 核参数与预测误差关系曲线Fig. 2 Relationship curve between kernel parameter and prediction error

序号核参数平均相对误差/%1102.9821021.7131033.0041043.3151053.3261063.32
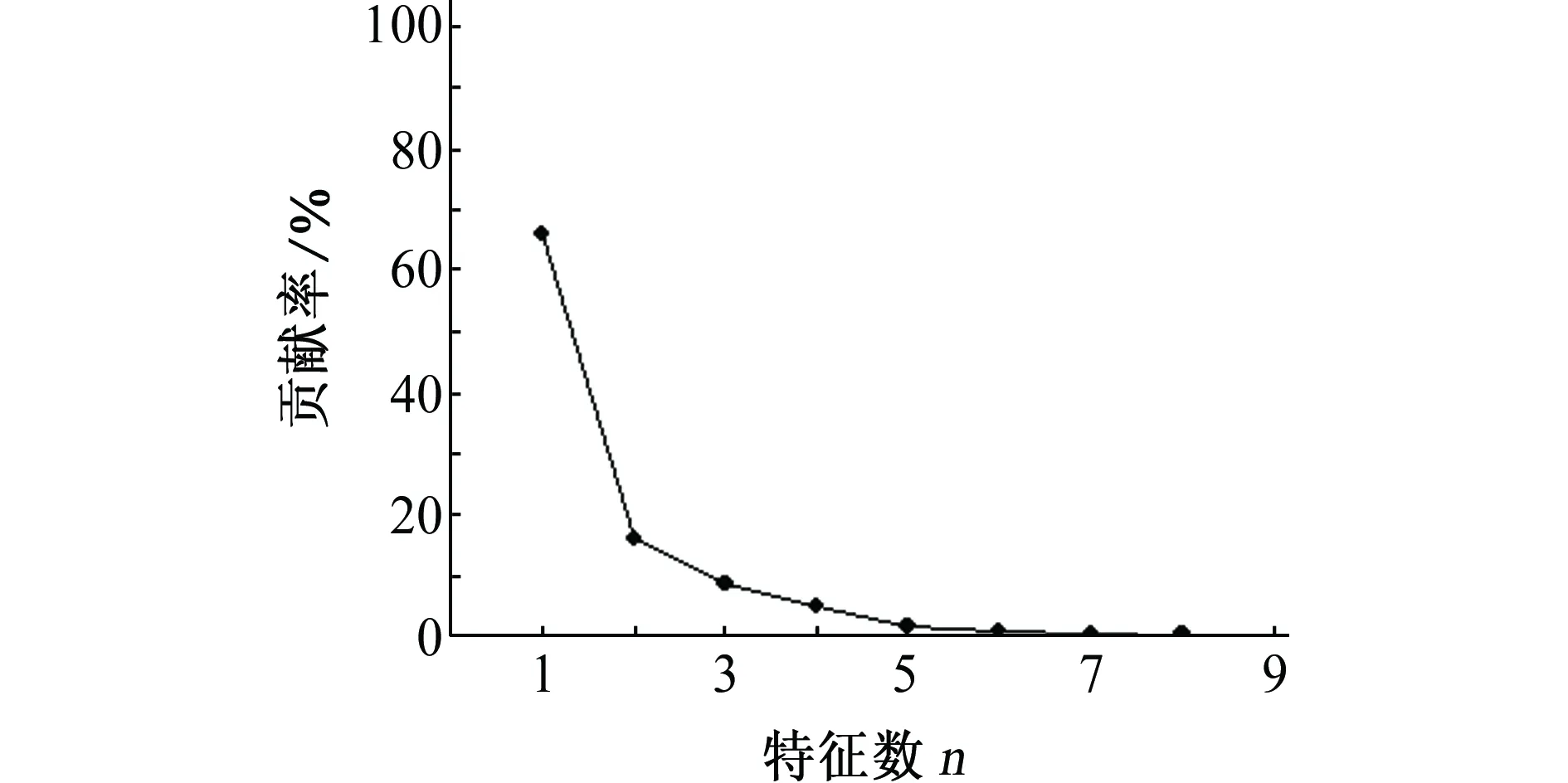
图3 特征值贡献率Fig. 3 Contribution rate of eigenvalues
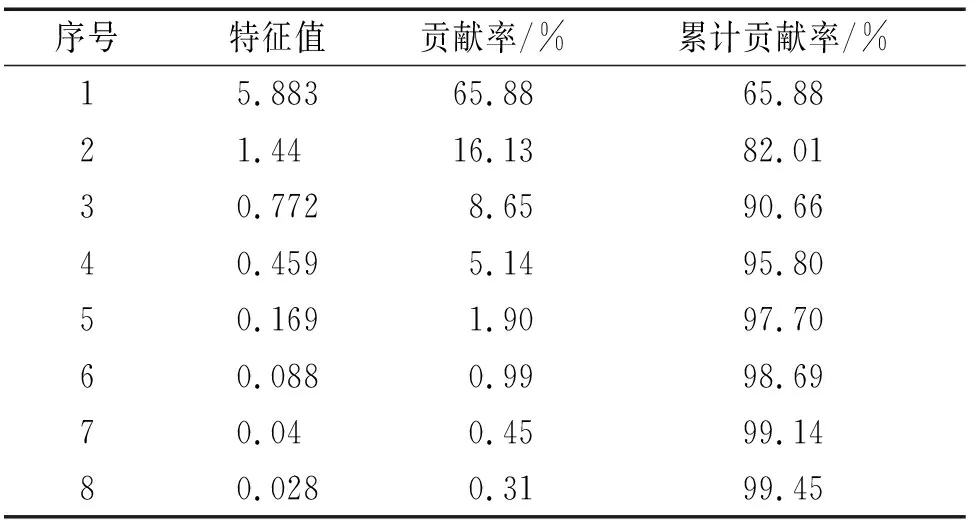
序号特征值贡献率/%累计贡献率/%15.88365.8865.8821.4416.1382.0130.7728.6590.6640.4595.1495.8050.1691.9097.7060.0880.9998.6970.040.4599.1480.0280.3199.45
3.3 模型预测效果检验
分别运用同类型管道b和c的工程数据,对管道a样本数据建立的KPCA-SVM预测模型进行检验,结果如图4所示。

(a) 管道b
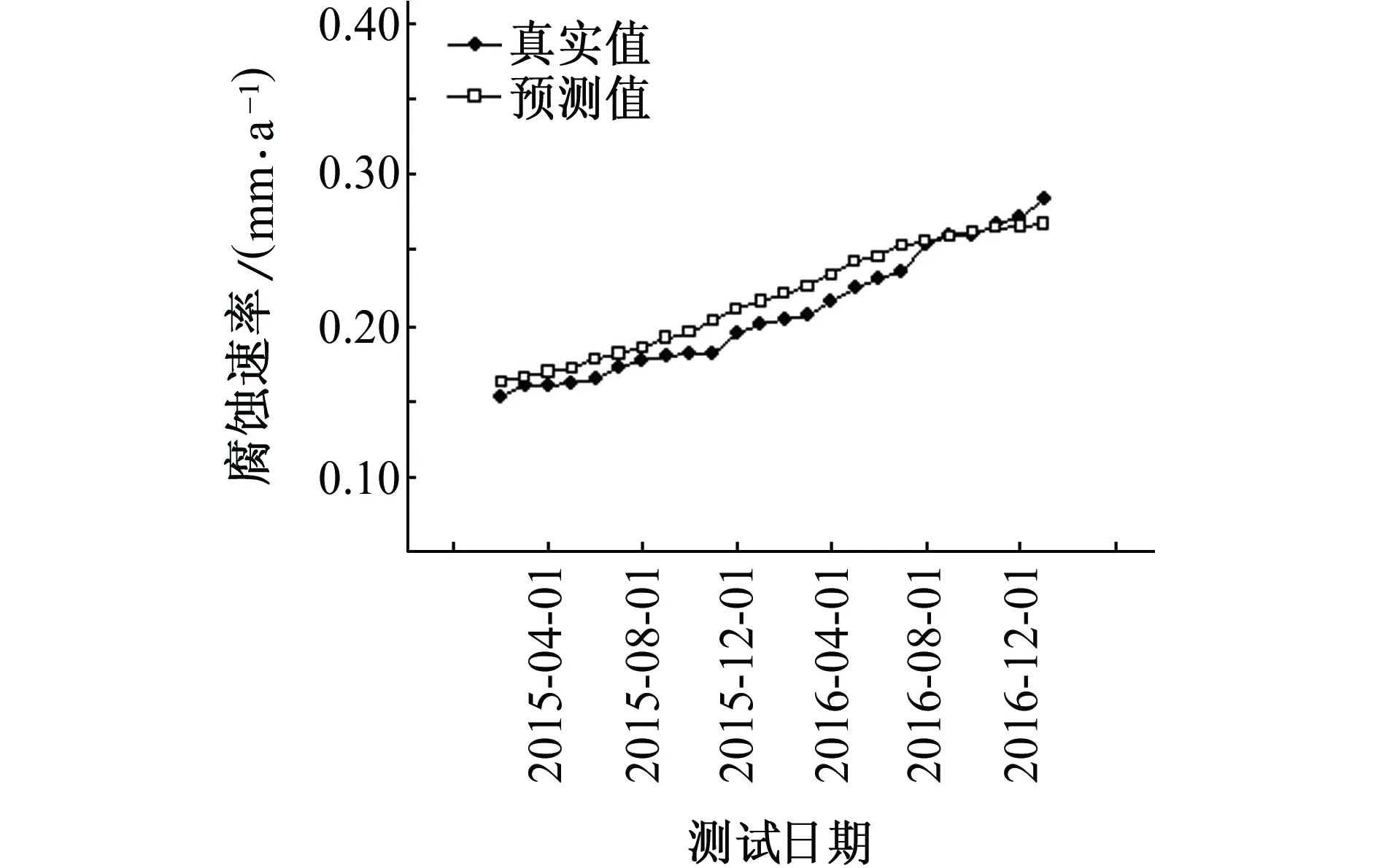
(b) 管道c图4 管道腐蚀速率预测结果Fig. 4 Prediction results of corrosion rate of pipeline
由图4可见:基于KPCA和SVM方法得到的预测腐蚀速率与真实腐蚀速率的趋势基本一致,对管道b、管道c的24个样本的腐蚀速率预测值均能良好地逼近真实值。为评定预测效果,根据式(13)~(15)分别计算预测结果的平均相对误差、绝对平均误差及方均根误差,计算结果如表4所示。
表4数据表明,KPCA-SVM模型在预测同类型管道腐蚀速率时的三类预测误差均较小,预测效果比较符合实际需求。
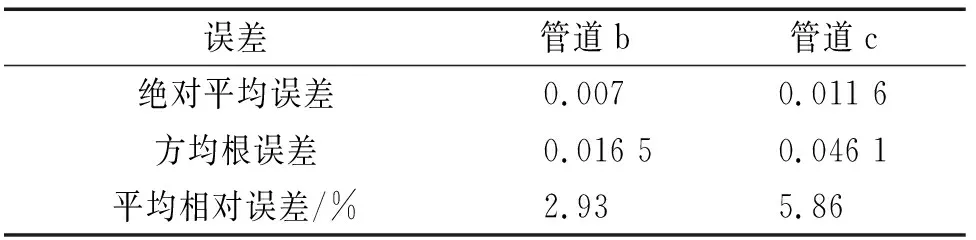
表4 腐蚀速率预测误差Tab. 4 Corrosion rate prediction error
4 结论
(1) 采用KPCA方法,降低了多种腐蚀影响因素间的冗余性,有效缩减了数据维数,为后续腐蚀速率预测奠定了基础。
(2) 当KPCA选用径向基核函数时,KPCA-SVM模型的预测误差随着KPCA核参数σ的增大先减小后增大,最后稳定不变。
(3) 由同类型管道实际工程数据对模型的预测效果的检验结果可知,基于KPCA和SVM方法建立的模型得到的管道腐蚀速率的预测值与真实值的吻合程度较高,三类误差均较小,符合实际要求。
