孔型几何参数对孔型密封泄漏和鼓风加热特性影响研究

方志,李志刚,李军,2

(1.西安交通大学能源与动力工程学院,710049,西安;2.先进航空发动机协同创新中心,100191,北京)

先进阻尼密封技术不仅能有效减小泄漏、提高透平机械的运行效率,还能增强转子系统安全稳定性,是现代透平机械关键部件之一[1]。目前,典型的阻尼密封技术有蜂窝、孔型和袋型密封。孔型密封具有与蜂窝密封相近的泄漏特性和气流激振动力特性,而且相比于焊接工艺复杂的蜂窝密封,孔型密封采用铣刀或电火花在金属材料上加工圆孔,具有制造工艺简单、成本低、结构可控性好、耐磨等优点[2]。因此,当前透平机械厂商逐渐倾向于采用铝质孔型密封代替蜂窝密封应用于多级离心压气机中[3]。

目前,针对孔型密封性能的研究主要集中其泄漏特性和转子动力特性方面[4-6]。Childs实验研究了孔深H=1.9,3.3,6.6 mm对孔径D=3.175 mm的孔型密封泄漏特性、转子动力特性的影响,结果表明:最小孔深时,孔型密封具有最小的泄漏量和最佳的转子动力特性[7]。Migliorini等通过CFD数值研究进一步证明了Childs等[7]的实验结果[8],并且阐明了孔深对孔型密封摩擦因子、泄漏量、转子动力系数的显著影响。在此基础上,Migliorini等数值研究了深径比对孔型密封泄漏量和摩擦因子的影响[9],结果表明:孔深径比影响了孔腔室内涡流和密封间隙流的结构,对泄漏量和摩擦因子影响显著。Vallnnarsdall实验研究了大孔径(D=12.26 mm)孔型密封的泄漏特性和转子动力特性[10],结果表明,与小孔径(D=3.175 mm)相比,大孔径孔型密封具有更大的有效阻尼,但泄漏量增大了37.5%。Childs实验研究了不同轴向变孔深结构对孔型密封泄漏特性和转子动力特性的影响[11],结果表明,与恒定孔深的孔型密封相比,合理设计的轴向变孔深孔型密封能够使泄漏量减小约20%。

密封鼓风加热效应是指在泄漏流通过密封间隙时,由于转子高速旋转和壁面的黏性阻力作用,导致泄漏流总温升高的现象[12]。鼓风加热效应使得燃气透平二次空气系统的冷却气体温度升高、冷却品质下降,进而影响高温部件的冷却效率和使用寿命。因此,研究密封鼓风加热特性是十分必要的。

实验测量和数值预测结果均表明,孔型密封设计中关键几何参数孔深、孔径对其泄漏特性和转子动力特性均具有显著影响,但对二者的耦合影响规律、作用机制还不明确。此外,目前国内外对关于孔型密封鼓风加热特性研究很少,限制了孔型密封在燃气透平二次空气系统中的应用。

1 计算模型和数值方法

1.1 计算模型

图1给出了孔型密封实验件几何结构[6]。密封静子面布置有孔径为3.175 mm、孔深为3.302 mm、总孔数为2 668、孔隙率为69%的交错排列的孔腔结构。表1给出了孔型密封实验件几何参数和实验工况。为研究孔深、孔径对孔型密封泄漏特性和鼓风加热特性的影响规律,以实验测量的孔型密封几何参数[7]为基准,保持密封直径和轴向长度恒定,设计了7种孔径(D=2,3.175,5,7,9,11,14 mm)的孔型密封结构,表2给出了不同孔径下,密封静子面上交错排列孔腔的分布规律和几何参数。图2给出了孔型密封三维计算模型,包含进出口延伸段。考虑到孔型密封结构的旋转周期性,计算域选取两个孔腔弧段,周向两个侧面采用旋转周期性边界。

图3给出了采用不同网格生成方法获得的两种孔深(H=3.175,6.6 mm)的孔型密封三维计算网格。传统网格生成方法(三维造型网格剖分)M1和本文提出的基于动网格技术和节点位移扩散方程的网格生成方法M2具有相同的网格质量,M2具有网格生成自动化程度高、速度快的优点。

(a)孔型密封三维结构 (b)孔腔结构参数 图1 孔型密封实验件几何结构[7]

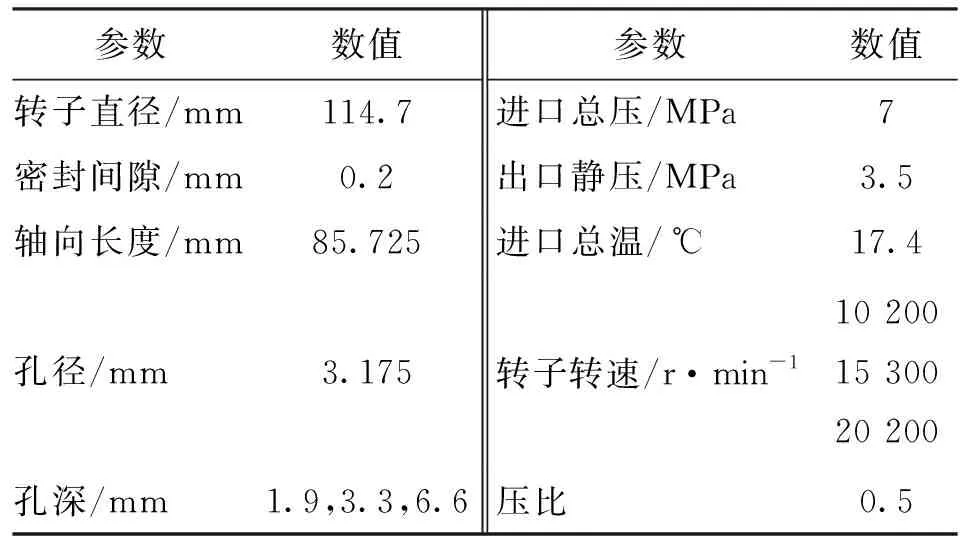
参数数值参数数值转子直径/mm114.7进口总压/MPa7密封间隙/mm0.2出口静压/MPa3.5轴向长度/mm85.725进口总温/℃17.4孔径/mm3.175转子转速/r·min-110 20015 30020 200孔深/mm1.9,3.3,6.6压比0.5

表2 孔型密封静子面孔布置参数

图2 D=11 mm、H=10 mm的孔型密封三维计算模型

图4给出了M2网格生成方法流程图。首先,采用三维造型软件UG生成不同孔径下、具有初始孔深(选取最小孔深H=0.5 mm)的孔型密封三维计算模型。然后采用ANSYS ICEM软件生成初始孔深的孔型密封三维多块结构化网格。基于动网格技术,采用ANSYS CFX求解节点位移扩散方程获得孔深连续变化(0.5 mm～15 mm)的孔型密封三维计算网格。节点位移扩散方程为

·(Γdispδ)=0

(1)

式中:δ为密封孔顶面节点径向位移;Γdisp为网格刚度,决定计算域内相邻网格节点一起移动的程度,网格刚度越大的区域,相邻节点间相对位移越小。网格刚度Γdisp由刚度模型决定,为保证边界层网格质量,本文选取基于网格控制体积的刚度模型

(2)

式中:Vref为参考控制体积,设为1 m3;V为控制体积;Cstiff为刚度模型指数系数。该刚度模型决定了网格刚度随着控制体积减小而呈指数增大,而Cstiff决定了网格刚度增大速率。在初始网格加密区域(如近壁面边界层区域),由于控制体积小,网格刚度大,相邻节点间相对位移很小,保证了孔深增大时,新生成的网格节点相对分布不变。因此,基于M2网格生成方法的孔型密封网格质量决定于密封初始网格质量。为保证较高的计算网格质量,初始密封网格对每个密封孔采用O型网格生成加密边界层。

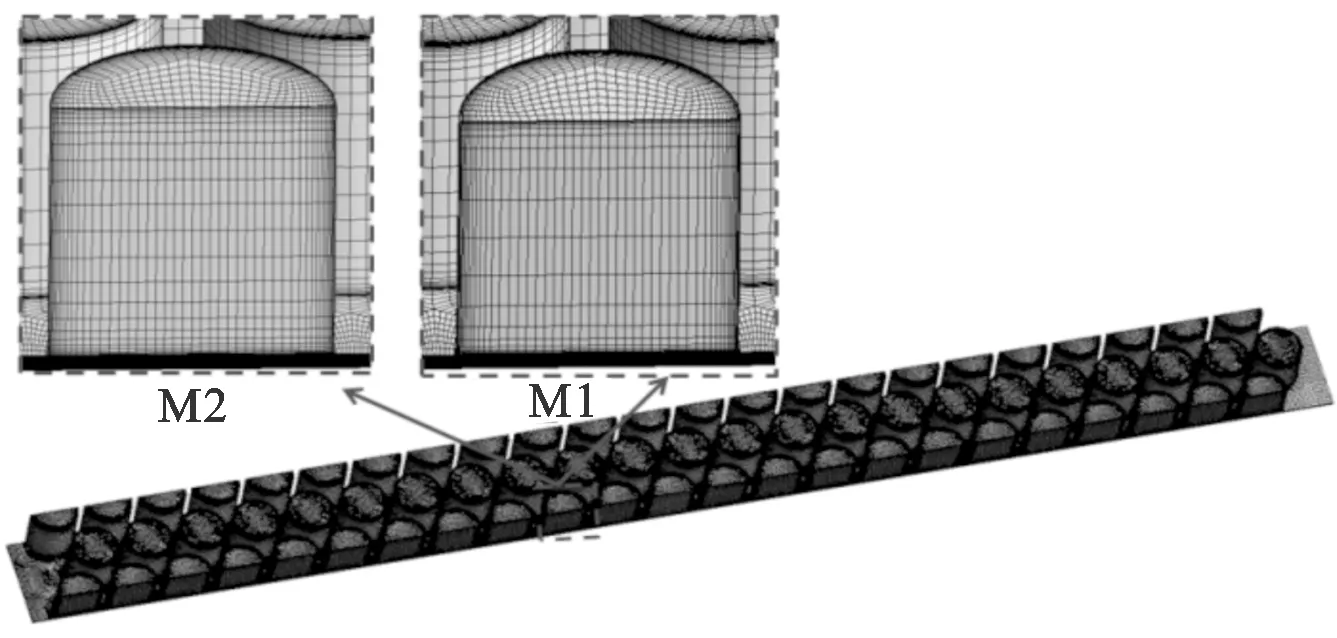
(a)H=3.3 mm

(b)H=6.6 mm图3 孔型密封三维计算网格(D=3.175 mm)

1.2 数值方法

采用提出的基于动网格技术和节点位移扩散方程的孔型密封网格生成方法、定常CFD数值计算方法,计算分析了孔径、孔深对孔型密封泄漏特性和鼓风加热特性的影响规律,流程图如图4所示。在ANSYS CFX中,通过求解RANS方程获得收敛的密封CFD流场、泄漏量和鼓风加热功率前,需先通过求解节点扩散方程获得新孔深参数下的密封计算网格,密封孔顶面节点径向位移方程为

δ=NstepΔδ

(3)

式中:Nstep为CFX求解器迭代步数;Δδ为密封孔顶面位移步长(孔深变化量)。基于动网格技术,采用用户自定义函数将式(3)代入ANSYS CFX中求解节点位移扩散方程,从而控制密封孔深。表3给出了具体的CFD数值方法和节点位移方程求解参数。

综上所述，在异位妊娠治疗中，应用阴道超声检查的价值显著，可以及时明确患者的异位妊娠详情，同时可为临床治疗方案提供参考信息，因此具有显著临床使用价值。

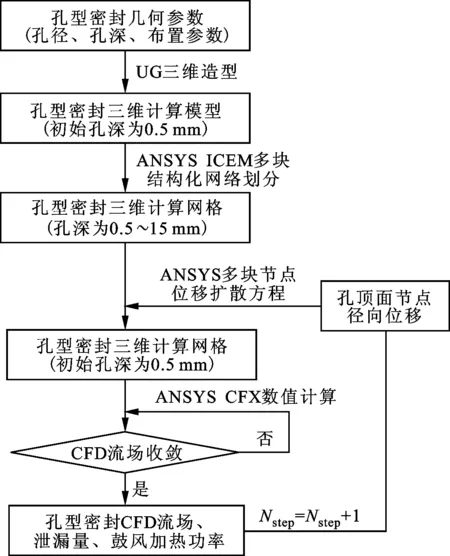
图4 M2网格生成方法和CFD数值方法流程图

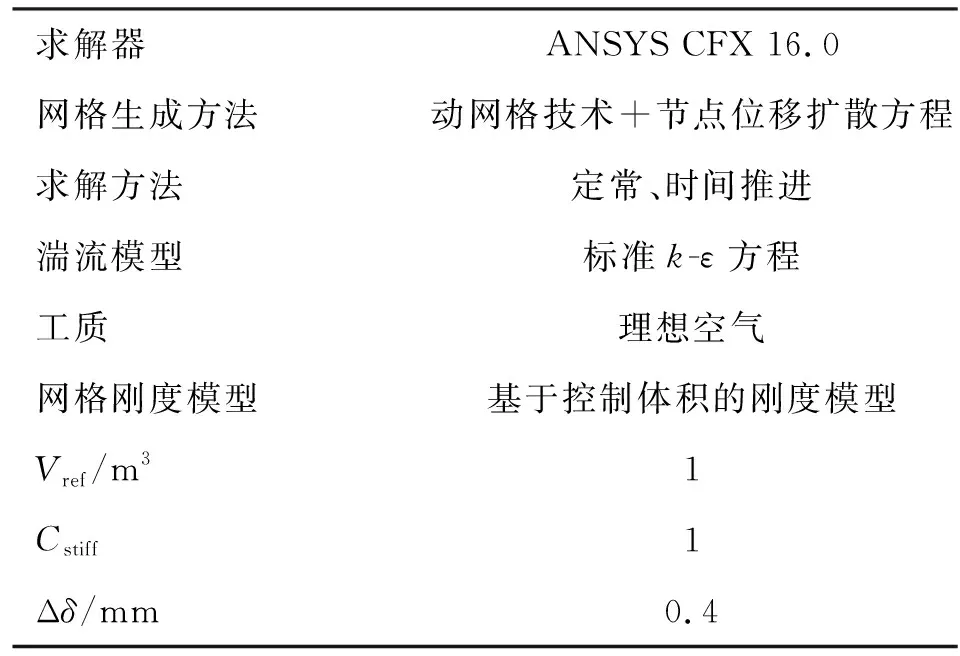
求解器ANSYS CFX 16.0网格生成方法动网格技术+节点位移扩散方程求解方法定常、时间推进湍流模型标准k-ε方程工质理想空气网格刚度模型基于控制体积的刚度模型Vref/m31Cstiff1Δδ/mm0.4

采用的网格生成方法和数值计算方法能够实现一次定常CFD计算获得孔深连续变化下的孔型密封流场结构、泄漏量和鼓风加热功率等,具有计算资源消耗少、计算速度快、可获得孔型密封泄漏特性和鼓风加热特性随孔深连续变化规律的优点。

2 结果与讨论

2.1 数值方法验证

采用孔径D=3.175 mm、孔深H=1.9 mm的孔型密封实验件为计算模型,生成4套不同的网格节点数网格,以泄漏量作为考核指标,在n=20 200 r/min的边界条件下,对网格无关性进行了验证。当网格节点数达到200万时,泄漏量变化小于1%,可认为泄漏量对网格节点数已具有无关性,泄漏量随网格节点数变化曲线如图5所示。本文对不同孔径、孔深的孔型密封设定网格节点数为185～270万,在密封间隙处沿径向布置了25个节点。

以孔径D=3.175 mm、孔深H=1.905 mm孔型密封3种转速下的泄漏量为考核指标,对湍流模型进行校核。如图6所示,k-ω和标准k-ε湍流模型计算结果与实验结果吻合良好,且具有相近的预测精度(误差小于2.0%)。文献[13]证明,相比于k-ω湍流模型,标准k-ε湍流模型对密封鼓风加热特性的预测精度更高。因此,综合考虑泄漏量和鼓风加热功率预测精度以及计算资源消耗,本文计算中选取了标准k-ε湍流模型。

图5 泄漏量随网格节点数变化曲线 (D=3.175 mm,H=1.9 mm)

图6 不同湍流模型泄漏量随转速变化曲线 (D=3.175 mm,H=1.9 mm)

为对所提出的基于动网格技术和网格节点扩散方程的孔型密封网格生成方法、定常CFD数值计算方法进行考核,本文采用传统网格生成方法和CFD数值计算方法计算了孔径D=3.175 mm的孔型密封实验件在n=20 200 r/min时,3种孔深(H=1.9,3.3,6.6 mm)下的泄漏量,同时采用本文提出的数值方法计算了孔深在0.5～10 mm范围内连续变化时的泄漏量,并与实验结果[7]进行了比较。如图7所示,本文提出的数值方法具有与传统数值方法相同的预测精度,均与实验结果吻合良好(误差小于2.0%,H=3.3 mm除外)。因此,本文数值方法能够准确预测孔型密封泄漏量随孔深的连续变化规律,且具有自动化程度高、计算速度快的优点。

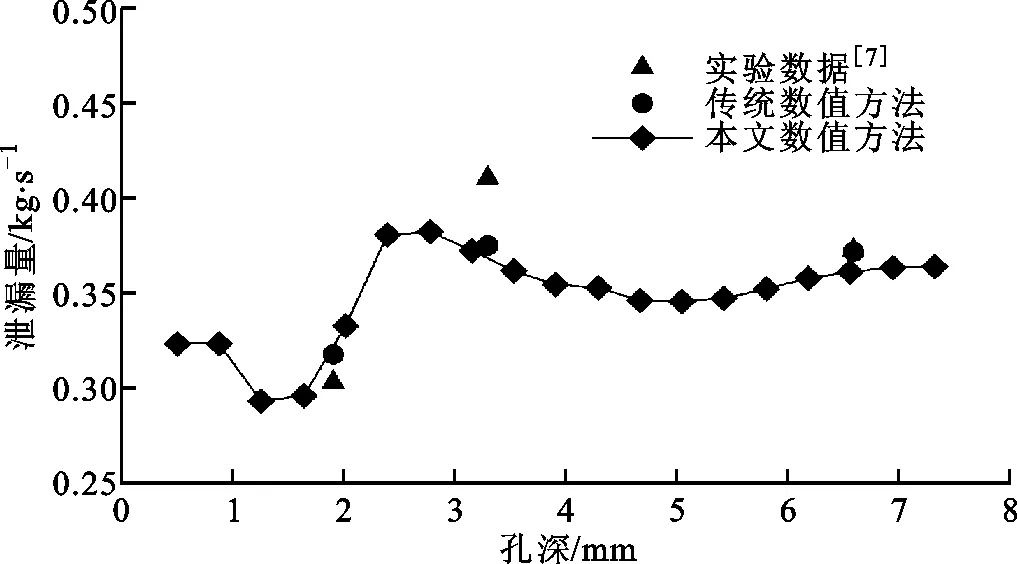
图7 两种数值方法密封泄漏量预测结果与实验值对比 (D=3.175 mm)

2.2 泄漏特性

为研究孔深、孔径对孔型密封泄漏量影响规律,计算分析了7种孔径(包括密封试验件D=3.175 mm)下,孔深在0.5～15 mm范围连续变化的232种孔型密封结构的泄漏量和流场结构,如表2所示。

图8给出了在5种不同孔深下,孔型密封泄漏量随孔径的变化。在不同孔深下,随孔径增大,孔型密封泄漏量均先略微减小,然后迅速增大。当孔径较小时(D为2～5 mm)当量密封齿数N(轴向孔腔数)较大,密封节流耗散作用显著,泄漏量较低,此时高速射流深入腔室的偏转角和腔室涡流结构是影响泄漏量的主要因素,随着孔径增加,射流偏转角增大,导致动能输运系数减小,泄漏量略微降低。当孔径较大(D为5～14 mm)时,N为影响泄漏的主要因素。随着孔径增加,轴向孔腔数减小,节流耗散作用减弱,泄漏量显著增大。密封孔径D从5 mm增加到14 mm时,当量密封齿数N从15减小到5,泄漏量增大了约50%。

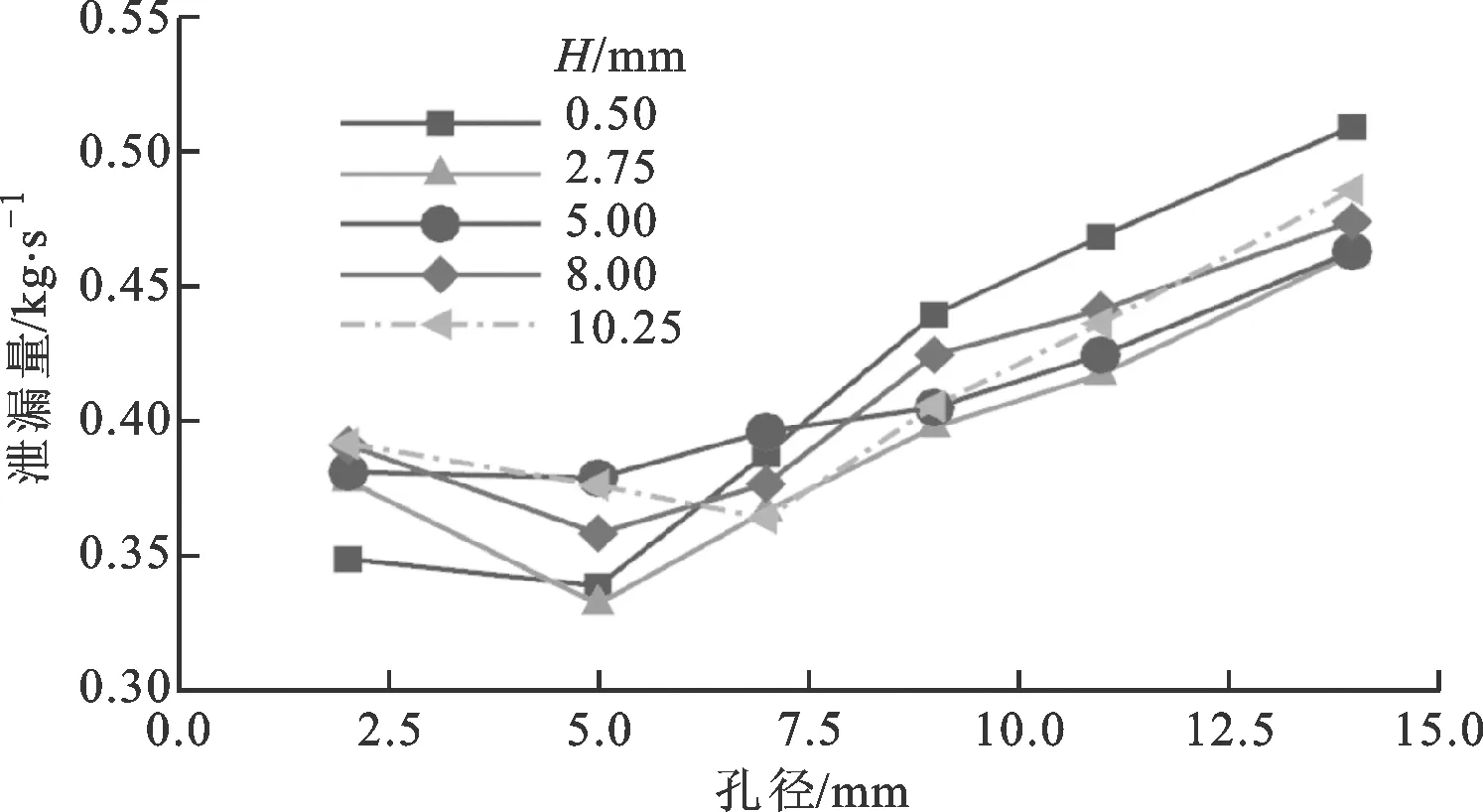
图8 泄漏量随孔径变化曲线

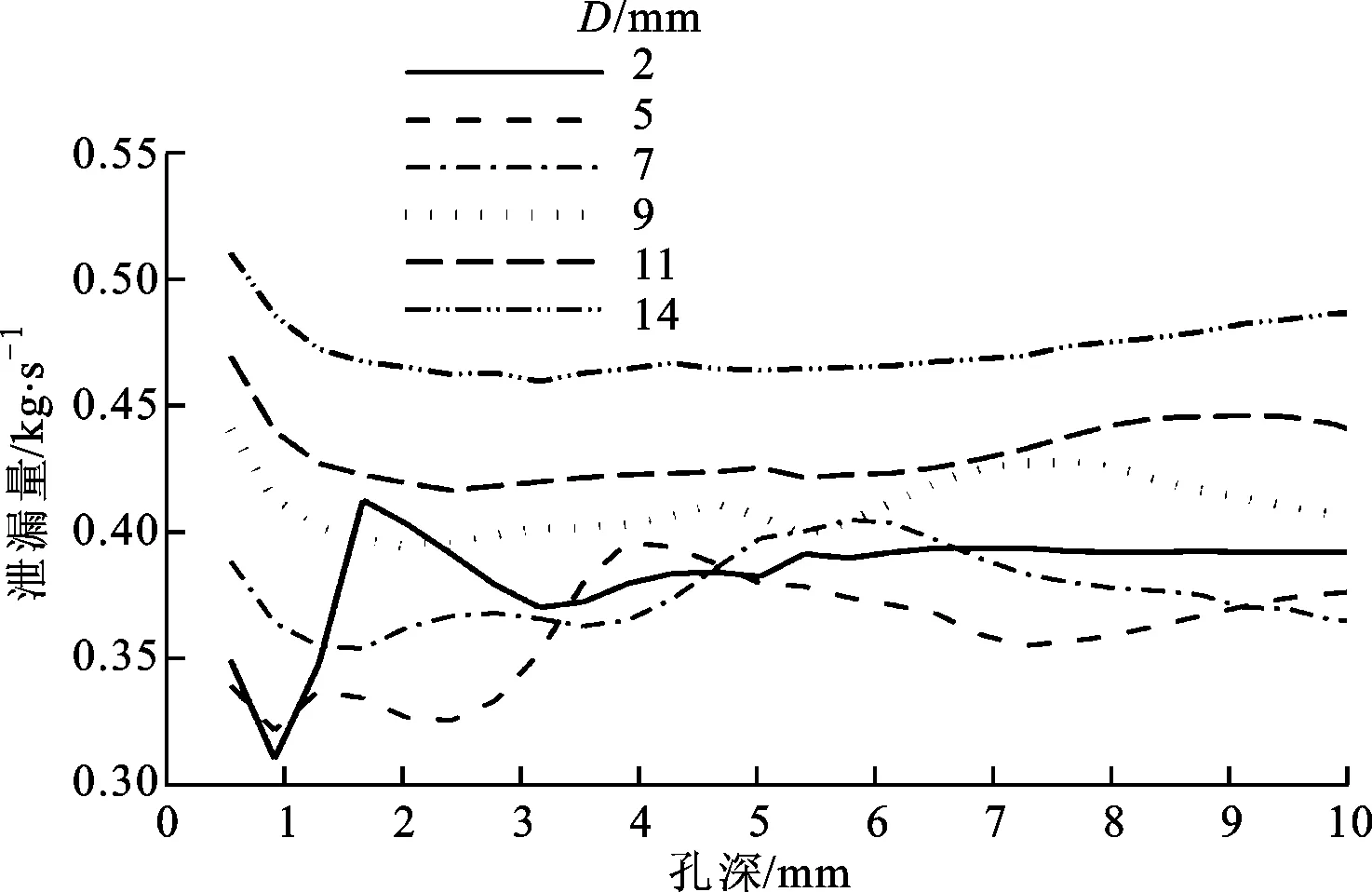
图9 泄漏量随孔深变化曲线

图9给出了在6种不同孔径下,孔型密封泄漏量随孔深的变化曲线。不同孔径下,随孔深增大,孔型密封泄漏量呈现先减小后增大、再减小的波动变化;当孔深增大到一定程度时,泄漏量趋于恒定值。孔径越小,泄漏量随孔深的波动越明显;孔径D=2 mm时,泄漏量随孔深波动幅度达32%。由图8、图9可知,孔型密封泄漏随孔径和孔深的变化规律均同时受到孔深、孔径的影响。这主要是因为密封孔腔内的流场结构、耗散强度受孔深、孔径耦合的影响。

考虑到孔型密封泄漏量同时受孔深、孔径影响,引入深径比AR对孔深、孔径的耦合影响进行评估。深径比为孔深与孔径的比值。图10给出了孔型密封泄漏量随深径比的变化曲线。由图10可知:随着AR增加,孔型密封泄漏量先迅速减小,然后经历两次先增加后降低的波动过程,最后趋于恒定值;孔径越小,泄漏量随深径比波动幅值越大;所有孔径下,孔型密封泄漏量均在AR=0.2附近取得最小值,在AR=0.8附近达到最大峰值;除最小孔径(D=2 mm)外,孔型密封泄漏量在AR在0.2～0.5范围波动很小(<5%),且在整个深径比范围内,孔型密封泄漏量均随孔径增大而增大。因此,从减小泄漏量的角度考量,孔型密封设计中孔径应控制在2～5 mm范围内,孔深应在0.2～0.5 mm范围取值。

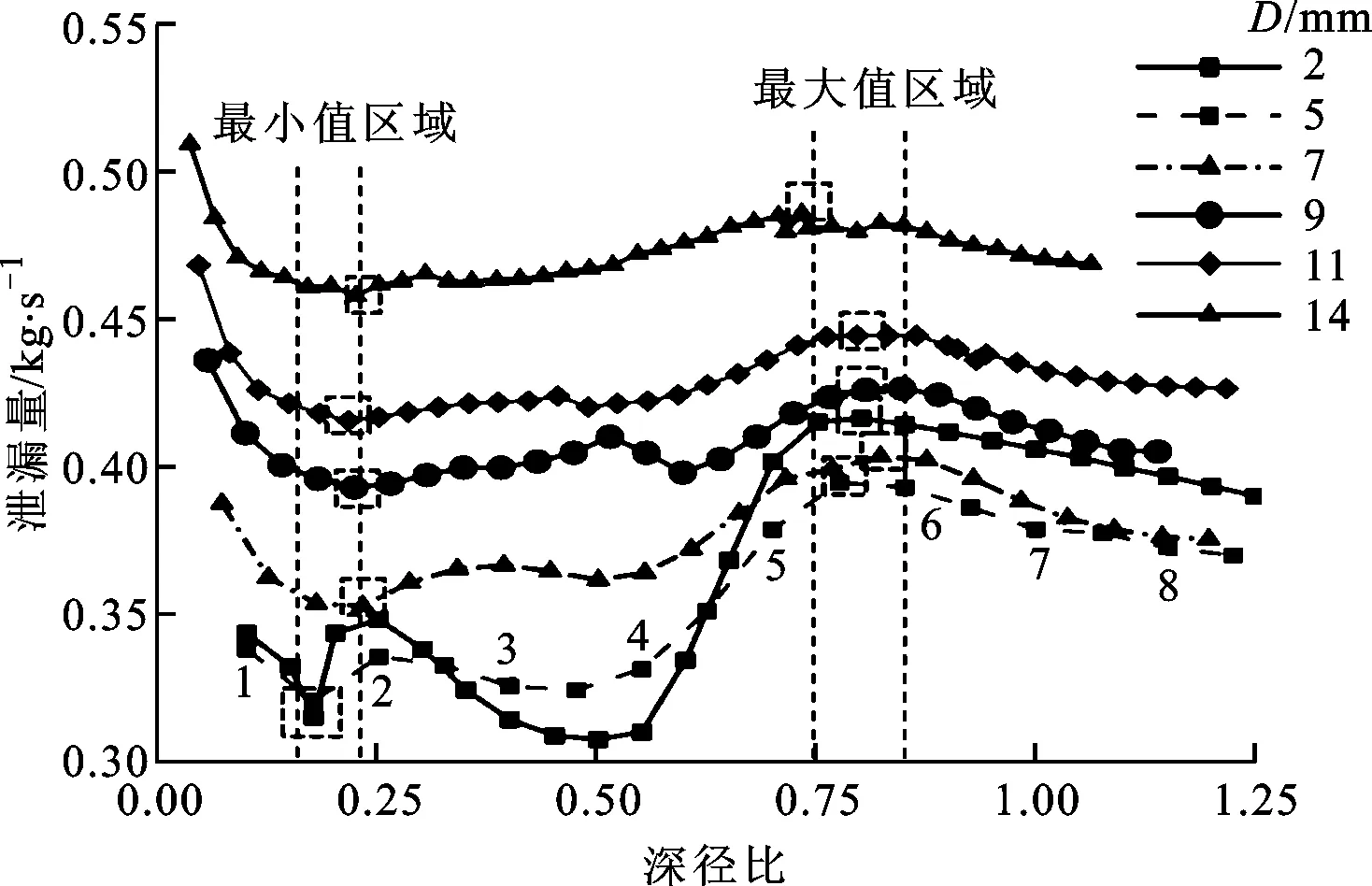
图10 泄漏量随深径比变化曲线

密封间隙处节流形成的高速射流流经孔型密封腔室会形成深入腔室内部的偏转角,并在下游腔室内壁上滞止产生分离线,如图11所示。分离线上侧流体进入腔室形成涡流耗散动能,分离线下侧流体不进入腔室内部,直接流入下游密封间隙通道。因此,高速射流深入孔型腔室的偏转角越大,进入腔室内部经涡流耗散的流体越多,动能输运系数越小,密封性能越好。

图11 孔型密封孔腔子午面流场和马赫数分布 (D=5 mm,H=2 mm)

为分析泄漏量随深径比AR变化的内在机理,图12给出了孔径为5 mm、8种深径比下,孔型密封轴向最后2个孔腔子午面流线和马赫数分布。由图12可知:随深径比增大,密封出口间隙马赫数呈现先减小后增大再减小的波动变化;孔腔内流场涡流尺寸逐渐增大,涡流结构也发生显著变化;涡流尺寸增大,涡流耗散作用增强,密封封严性能提升;涡流结构在AR=0.55时从单涡核演变为耗散作用更强的双涡核,并在AR=0.7时减弱为单涡核;涡流结构的显著变化导致泄漏量急剧变化;随AR增加,射流偏转角先减小再增大,最后逐渐减小并趋于平稳;射流偏转角增大,表明深入腔室内部经涡流耗散的流体越多,动能输运系数越小,密封性能越好;当AR大于1时,腔室涡流结构基本稳定,涡流尺寸略微增大,但相对变化量逐渐减小,射流偏转角也基本不变,因此孔型密封泄漏量略微下降并逐渐趋于稳定。

2.3 鼓风加热特性

在燃气轮机和航空发动机的二次空气系统中,密封的主要作用是调控冷却气流的流量、对冷气进行组织和分配,防止燃气入侵。密封的鼓风加热效应,即密封转子损失的机械能转化为泄漏流的内能,会导致冷却温度上升,冷却品质下降,威胁热端部件的运行寿命;输出功减少,运行效率降低。因此,关注孔型密封泄漏特性和转子动力特性的同时,准确预测其鼓风加热特性对保证燃气透平运行效率和高温部件运行寿命是十分必要的。

AR=0.1

AR=0.25

AR=0.4

AR=0.7

AR=0.85

AR=1

AR=1.15图12 孔型密封轴向最后2个孔腔子午面流线和 马赫数分布(D=5 mm)

(4)

图13给出了5种孔径下,鼓风加热功率随孔深的变化。由图13可知,随孔深增大,鼓风加热功率总体呈现减小趋势。相同孔深、孔径较小时(D为2～9 mm),鼓风加热功率随孔径增加而增大;孔径较大时(D为9～14 mm),鼓风加热功率随孔径变化很小。因此,从减小转子耗功和泄漏流温升的角度,孔型密封应选取较小的孔径(D为2～5 mm)和较大的孔深。

图13 鼓风加热功率随孔深变化曲线

3 结 论

本文提出了基于动网格技术和节点位移扩散方程的变孔深孔型密封三维计算网格的生成方法,以及基于RANS方程的孔型密封泄漏量和鼓风加热功率的数值计算方法,计算分析了孔深、孔径对孔型密封泄漏特性、鼓风加热特性的影响规律。研究结果可为孔型密封设计中关键几何参数孔深、孔径的选取提供理论依据。得到如下结论。

(1)本文提出的基于动网格技术和节点位移扩散方程的孔型密封网格生成方法、定常CFD数值计算方法能够准确预测孔型密封泄漏量随孔深的连续变化规律,且具有自动化程度高、计算速度快的优点。

(2)孔型密封泄漏随孔径和孔深的变化规律均同时受到孔深、孔径的耦合影响;孔型密封深径比AR是影响孔型密封泄漏量的关键几何参数,且孔径越小,深径比影响越显著;随深径比AR增大,密封泄漏量会先降低,然后经历两次先增加后降低的波动,最后趋于平稳;孔型密封泄漏量在AR为0.15～0.25时,取得最小值,在AR为0.7～0.9时,取得最大值。

(3)随孔深增大,孔型密封鼓风加热功率总体呈现逐渐减小趋势。相同孔深下,孔径较小时(D为2～9 mm),鼓风加热功率随孔径增加而增大;孔径较大时(D为9～14 mm),鼓风加热功率随孔径变化很小。

(4)从减小密封泄漏、转子耗功和泄漏流温升综合考虑,孔型密封设计中应在D为2～5 mm范围内选取较小的孔径,在AR为0.2～0.5范围选取较大的孔深。