混合弹流润滑修形斜齿轮齿面摩擦功率损耗
2019-02-14张西金方宗德郭芳杨涛
张西金,方宗德,郭芳,杨涛
(西北工业大学机电学院,710072,西安)
斜齿轮具有重合度大、承载能力强等特点,因而在工业领域得到了广泛的应用。齿轮修形可以改善齿轮的传动性能[1-2],其不仅应提高齿轮的承载能力、减小传动误差及振动,而且应具有较小的齿面摩擦力,以便齿轮达到最好的综合性能。因此,研究修形斜齿轮的齿面摩擦功率损耗具有重要意义。
近年来,斜齿轮修形研究取得了一定进展。Litvin等提出了一种新的拓扑修形齿面,采用齿轮接触分析(TCA)技术进行了接触路径和传动误差分析,并应用有限元接触分析方法研究了轮齿弯曲应力和接触应力[3]。Velex等研究了高重合度锥齿轮的齿廓修形公式,可基于传动误差波动量设计最优的修形量[4]。Eritenel等研究了包含齿廓和齿向修形的齿轮非线性振动特性[5]。方宗德推导了修形斜齿轮的齿面接触与边缘接触的全部计算,探讨了齿面修形对改善齿轮传动性能的作用,并在TCA的基础上提出了一种结合有限元方法和非线性数学规划方法的齿轮承载接触分析(LTCA)技术,应用该技术对修形斜齿轮进行了计算,探讨了刀具修形及数字控制机床修形2种方法[2,6]。蒋进科等通过理论齿面叠加修形齿面,基于TCA和LTCA技术,建立动力学模型,通过三维修形完成了宽斜齿轮多目标齿面优化[7]。Baglioni等采用Niemann公式及完全弹流润滑公式分析了锥齿轮的齿顶修形效率[8]。Diez-Ibarbia等采用Niemann和混合弹流润滑2种摩擦系数公式研究了修缘锥齿轮的效率[9]。
综上所述,目前国内外的齿轮修形技术研究主要集中在传动性能、承载能力等方面,由于修形齿轮的润滑问题较复杂,对修形齿轮的效率研究较少,尤其是混合弹流润滑情况下各种修形齿轮的效率研究。本文在混合弹流润滑情况下,研究了修形斜齿轮的齿面摩擦功率损耗计算方法、修形参数对功率耗损的影响,可为斜齿轮修形设计提供一定的参考。
1 斜齿轮修形
斜齿轮修形包括齿廓修形、齿向修形和拓扑修形3种形式。齿廓修形通过改变齿轮刀具切削刃的形状实现。通常情况下,齿轮刀具常规的直线形切削刃改变为圆弧形、抛物线形等形式。本文研究的圆弧形齿廓修形,即为齿轮刀具切削刃在法平面内为圆弧形,而且只针对小轮修形。建立如图1所示的动坐标系,可以看出:2个坐标系建立在固定于小轮的加工刀具齿条上;xc10-oc10-yc10为齿条齿宽中心处的法平面,采用圆弧形切削刃;R为圆弧半径,R越小则修形量越大;圆弧与原来的直线形切削刃相切,切点和节线与直线形切削刃的交点的距离为c;a为节线上的法向半齿厚;θ1为圆弧切削刃上的点半径方向与yc10轴的夹角。节线上下工作齿面的修形量应不同,一般要求齿根部位齿面的修形量小于齿顶部位齿面的修形量,以确保修形不会明显减小齿根弯曲疲劳强度。
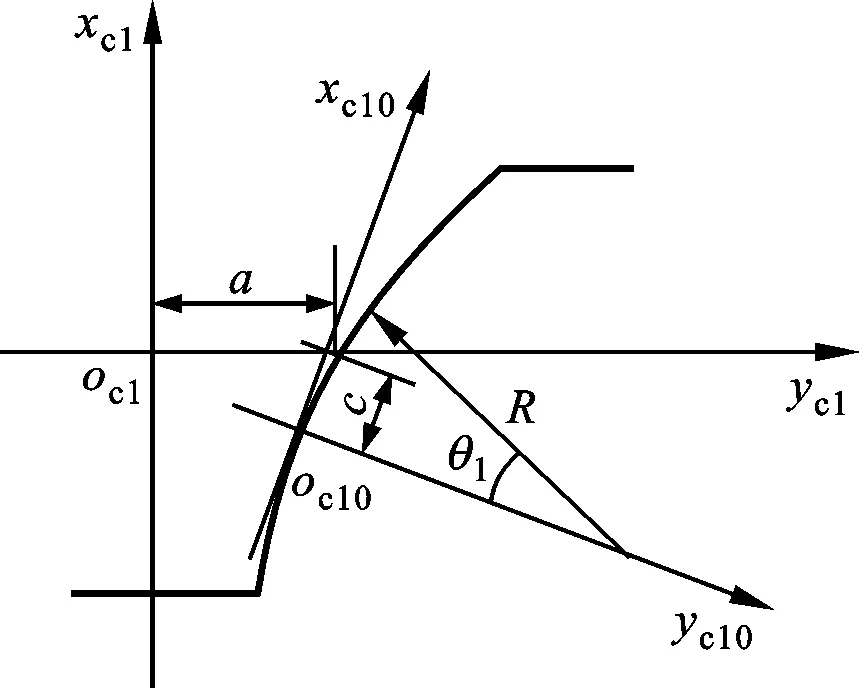
图1 修形刀具齿形
齿向采用鼓形修形,中间段采用直线,两侧采用曲线,本文采用四阶修形曲线。齿向修形如图2所示,其中:δ为齿向各点修形量;δmax齿向最大修形量;L为齿向各点修形长度;Lmax为齿向最大修形长度;b为齿宽。
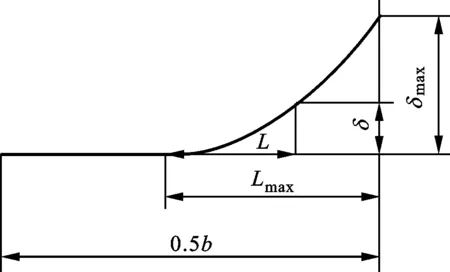
图2 齿向鼓形修形
在圆弧形齿廓刀具展成加工齿轮的基础上,齿向采用鼓形修形,形成拓扑修形。3种修形的示意图见图3。

(a)齿廓修形
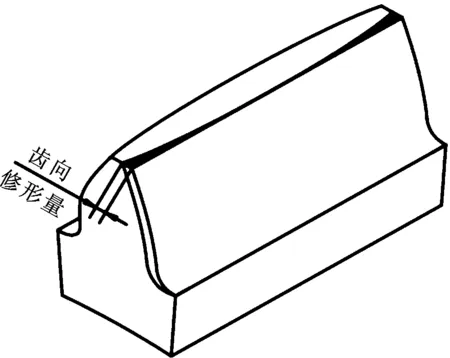
(b)齿向修形
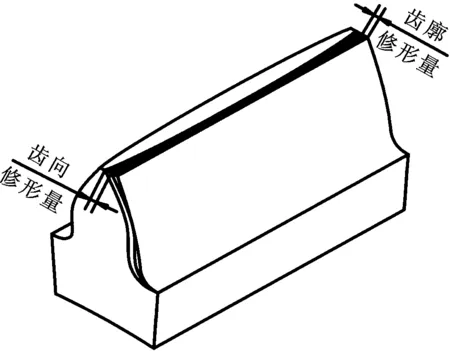
(c)拓扑修形图3 斜齿轮修形示意图
在xc10-oc10-yc10平面中,刀具齿面的四元位矢rc10表示为
(1)
式中:u1为xc10坐标值;v1为zc10坐标值。
采用对称的齿向修形方式,即齿向两侧的最大修形量和最大修形长度分别相同。齿向修形公式为
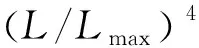
(2)
2 齿面摩擦功率损耗模型
2.1 齿面摩擦功率损耗
齿面摩擦功率损耗主要由齿轮啮合点间存在的相对滑动造成。不考虑其他功率损耗,混合弹流润滑条件下,1对齿轮啮合时齿面摩擦功率损耗的计算公式为
Wf=μML,ψ(ψ)Fn,ψ(ψ)vs,ψ(ψ)
(3)
式中:ψ为小轮转动角度,对应齿面上某个啮合点;μML,ψ(ψ)是混合弹流润滑条件下对应啮合点处的摩擦系数;Fn,ψ(ψ)为对应啮合点处的法向力;vs,ψ(ψ)为对应啮合点处的滑动速度。
式(3)仅考虑了1对齿轮的啮合情况,实际上斜齿轮重合度都大于1,在某一瞬时可能会有几对轮齿同时参与啮合,而且各齿轮的摩擦情况不同。若某一瞬时有m对齿轮同时啮合,则齿轮的瞬时齿面摩擦功率损耗可以定义为
(4)
2.2 摩擦系数
摩擦系数是影响功率损耗的一个重要因素,不同润滑状态下的摩擦系数不同。齿轮工作过程中一般处于混合弹流润滑状态,混合弹流润滑摩擦系数可以通过边界润滑摩擦系数和弹流润滑摩擦系数加权和的形式表示。小轮不同转角对应不同的齿面啮合点,在第i个啮合点混合弹流润滑摩擦系数μML(i)[9-10]定义为
μML(i)=μFL(i)fλ(i)+μBDR[1-fλ(i)]
(5)
fλ(i)=1.21λ(i)0.64/[1+0.37λ(i)1.26]
(6)
λ(i)=hc(i)/Ra
(7)
式中:μFL(i)为弹流润滑摩擦系数;fλ(i)为摩擦系数分配系数;μBDR为边界润滑摩擦系数,取0.227 098[9,11];hc(i)为中心油膜厚度;Ra为齿面等效平均粗糙度。
修形齿轮为点接触啮合,接触印痕为椭圆,因此中心油膜厚度[12]计算公式为
hc(i)=2.69Rx(i)U0.67(i)G0.53Q-0.67(i)·
(1-0.61e-0.73κ)φt(i)
(8)
(9)
vr(i)=|vp(i)+vg(i)|/2
(10)
G≈αE′
(11)
(12)
式中:μ0为环境黏度;vr(i)为滚动速度;νp(i)和νg(i)分别为啮合点处小轮和大轮的速度;α为压力黏度系数;W(i)为法向载荷;κ为椭圆率;φt(i)为考虑温度影响的修正系数,计算公式见文献[13];Rx(i)为啮合点处等效半径,可由啮合点处小轮和大轮的曲率半径ρp(i)和ρg(i)计算得到;E′为等效弹性模量,可由小轮和大轮的弹性模量E1、E2,泊松比ν1、ν2计算得到。Rx(i)和E′的计算公式为
(13)
(14)
弹流润滑状态是两齿面完全被油膜分开的理想状态,此时摩擦系数最小,功率损耗最小。Xu对弹流润滑状态进行了大量研究工作,获得的弹流润滑摩擦系数计算公式[14]为
(15)
f(Rs,r(i),Ph(i),η,Ra)=b1+b4|Rs,r(i)|·
Ph(i)log(η)+b5e-|Rs,r(i)|Ph(i)log(η)+b9eRa
(16)
(17)
vs(i)=|vp(i)-vg(i)|
(18)
式中:Rs,r(i)为齿面速度滑滚比;Ph(i)为齿面啮合点接触应力;η为润滑油的动态黏度;b1=-8.916 465,b2=1.033 03,b3=1.036 077,b4=-0.354 068,b5=2.812 084,b6=-0.100 601,b7=0.752 755,b8=-0.390958,b9=0.620 305;ve(i)为卷吸速度,ve(i)=|vp,t(i)+vg,t(i)|/2,其中vp,t(i)和vg,t(i)分别为啮合点小轮速率和大轮速度在切面上的投影分量;vs(i)为齿面相对滑动速度。
3 齿面摩擦功率损耗模型参数
齿面摩擦功率损耗模型的主要参数通过TCA及LTCA获得。通过TCA可以得到的参数包括:小轮接触椭圆短轴方向曲率半径ρp、大轮接触椭圆短轴方向曲率半径ρg、小轮啮合点速度vp、大轮啮合点速度vg、椭圆率κ等。通过LTCA可以得到的参数包括齿面啮合点的赫兹应力Ph、法向力Fn(θ)等。
小轮转速取为5 000 r/min,力矩取为450 N·m,等效弹性模量取为219 700 MPa,小轮和大轮齿面粗糙度取为0.35 μm,压力黏度系数取为9.68 GPa-1,环境黏度取为0.135 Pa·s,黏温系数取为0.021 7 K-1,润滑油热导率取为0.117 6 W/(m·K)。
齿轮基本参数为:小轮齿数30,大轮齿数45,法面模数6,压力角20°,螺旋角15°。该对齿轮副理论上有3对齿同时啮合,假设小轮和大轮的每个齿面上有15个瞬时啮合位置。图4表示小轮齿面上的啮合位置,编号1~15表示啮合顺序,小轮沿啮合线从齿根到齿顶依次有15个瞬时啮合位置,大轮齿面上对应的各啮合位置编号与小轮啮合位置编号相同。
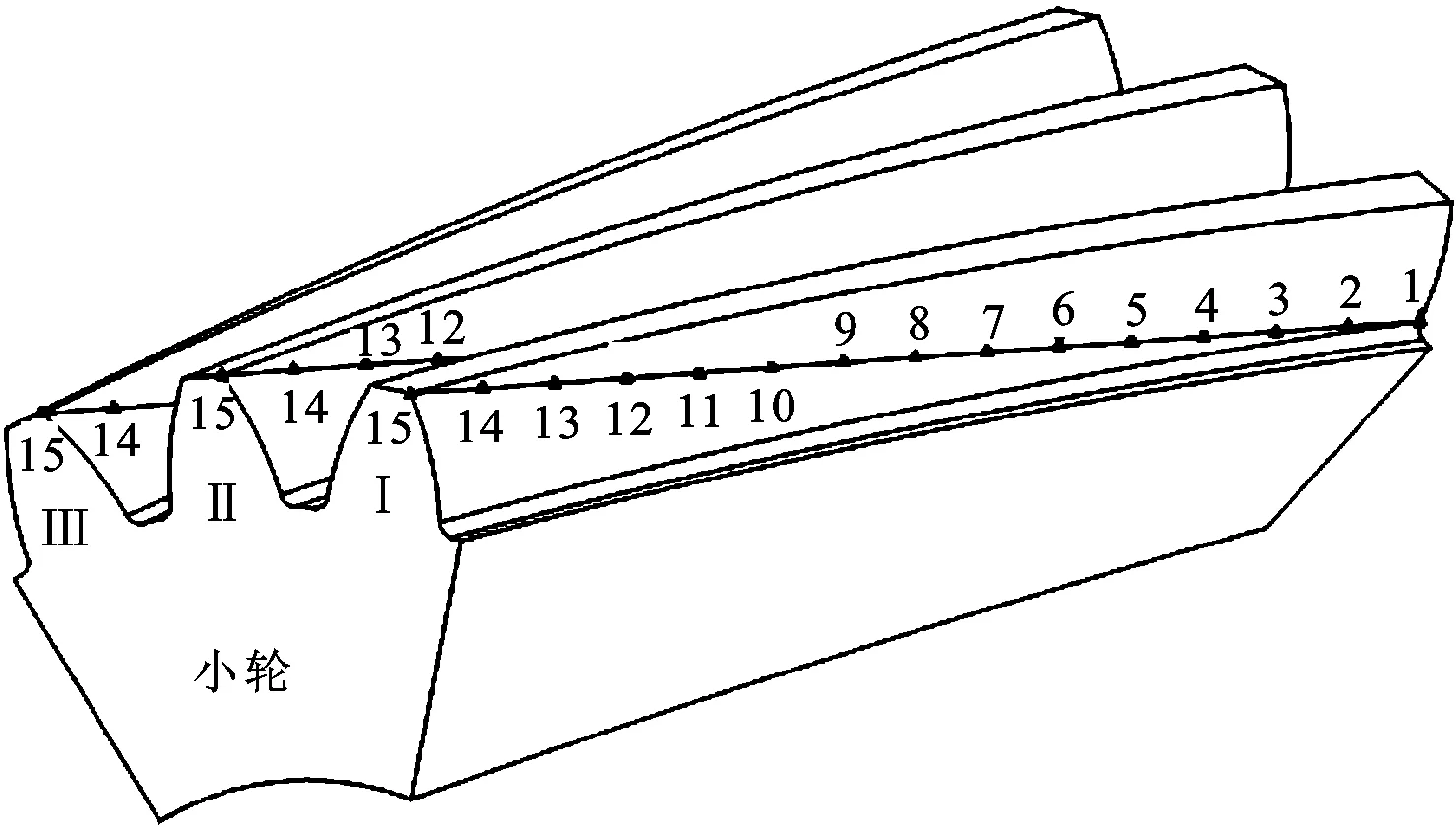
图4 小轮各瞬时啮合位置
假设φT为小轮在一个啮合周期内转过的角度,将φT等分为5份,若用φ表示小轮转角,则该对齿轮副理论上各瞬时啮合情况如表1所示。
4 修形斜齿轮的齿面摩擦功率损耗
4.1 齿廓修形斜齿轮的齿面摩擦功率损耗
设计圆弧半径R=K1mn,式中K1为齿廓修形

表1 轮齿副理论上各瞬时啮合情况
参数,mn为法向模数,为了不影响接触强度,圆弧半径不应太小。在R为150mn和250mn两种条件下,对齿廓修形斜齿轮的齿面摩擦情况进行仿真,结果如图5所示。为使齿根部位修形量小于齿顶部位修形量,c取为0.5 mm。若第i个啮合位置处接触椭圆长轴上的离散载荷pi,j(j=1,…,k)由LTCA计算得出,P为法向总载荷,则该啮合位置处的载荷分配系数计算公式为
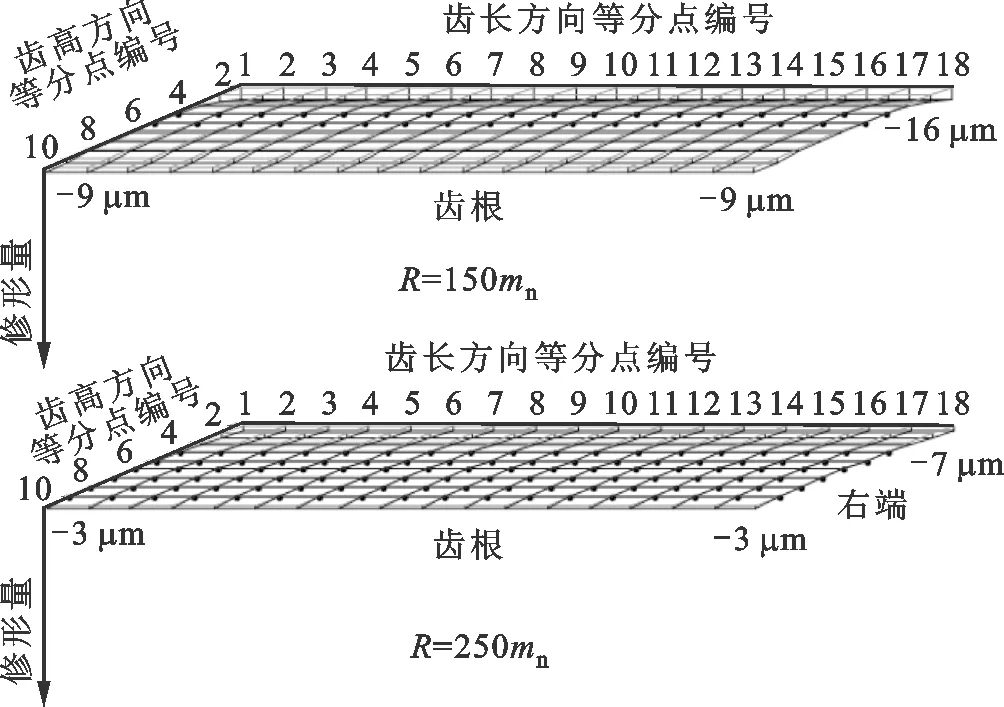
(a)齿廓修形量

(b)载荷分配系数

(c)摩擦系数分配系数
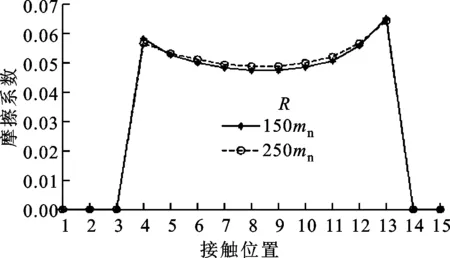
(d)摩擦系数
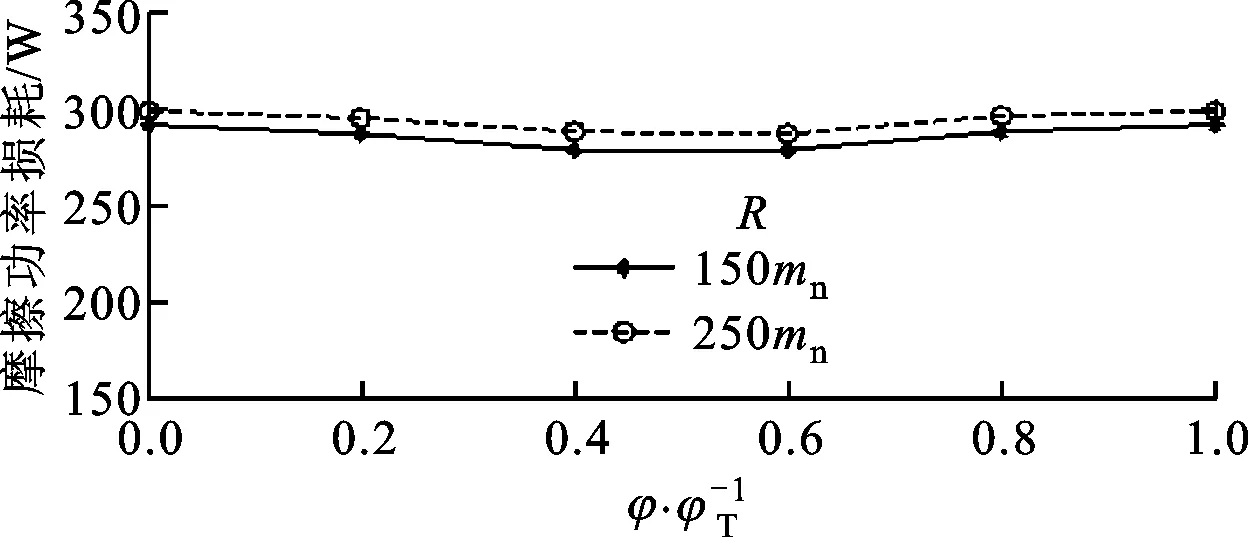
(e)摩擦功率损耗图5 齿廓修形斜齿轮的齿面摩擦情况

(19)
从图5a可以看出,齿顶修形量比齿根修形量大,这样的修形对齿根弯曲强度影响小。从图5b可以看出,啮合点1、2、3、14和15实际没有进入啮合状态,结合表1可以知道小轮转角各位置实际只有2对齿啮合。从图5c可以看出,两侧未实际啮合的点完全被润滑油膜隔开,摩擦系数分配系数为1;中间接触区域摩擦系数分配系数在0.71~0.81之间,处于混合摩擦状态,且以弹流润滑占为主。从图5d可以看出:由于两侧未实际啮合的点完全被润滑油膜隔开,所以接触应力为0,弹流润滑摩擦系数为0,摩擦系数也为0;在实际啮合点中,最中间位置摩擦系数稍小,修形量对摩擦系数影响较小。从图5e可以看出,在载荷、摩擦系数、滑动速度和啮合状态共同作用下,小轮转角在0.4φT和0.6φT时功率耗损较小。综上所述,修形量变化对功率耗损影响较小,齿廓修形引起的功率损耗波动较小,对传动有利。
4.2 齿向修形斜齿轮的齿面摩擦功率损耗
齿向修形参数包括最大修形量和最大修形长度。对于高精度齿轮,ISO推荐的齿向鼓形最大修形量为10~25 μm[15]。在相同的修形长度下,由于修形量很小,对功率损耗的影响也很小,所以本文仅研究修形长度对功率损耗的影响。取最大修形量为25 μm,在最大修形长度为0.1b和0.5b两种条件下,对齿向修形斜齿轮的齿面摩擦情况进行仿真,结果如图6所示。
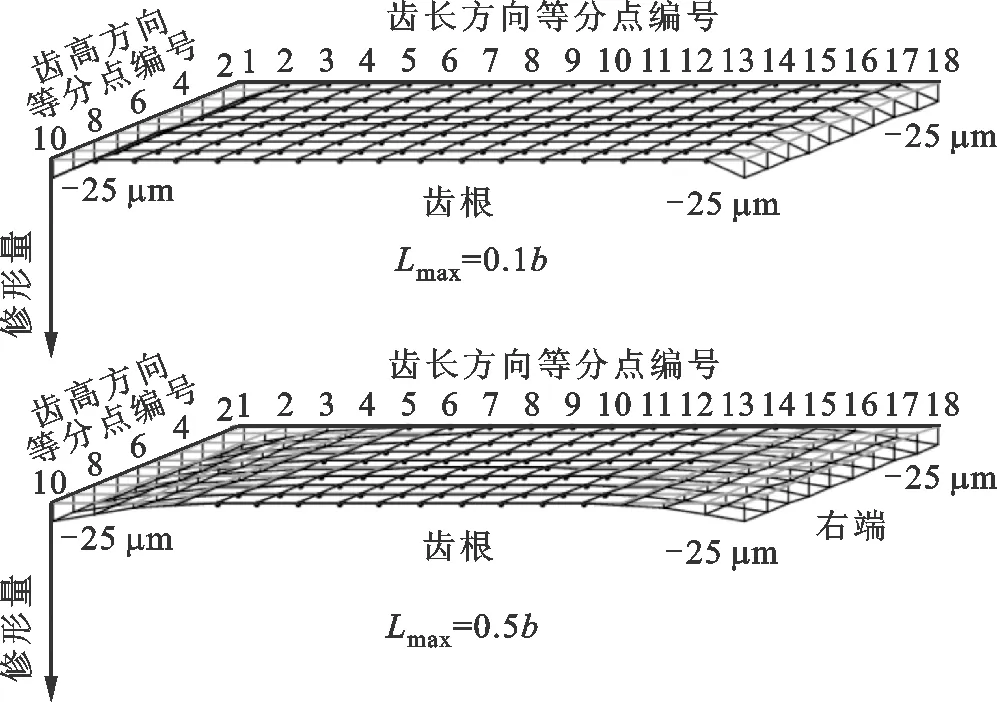
(a)齿向修形量
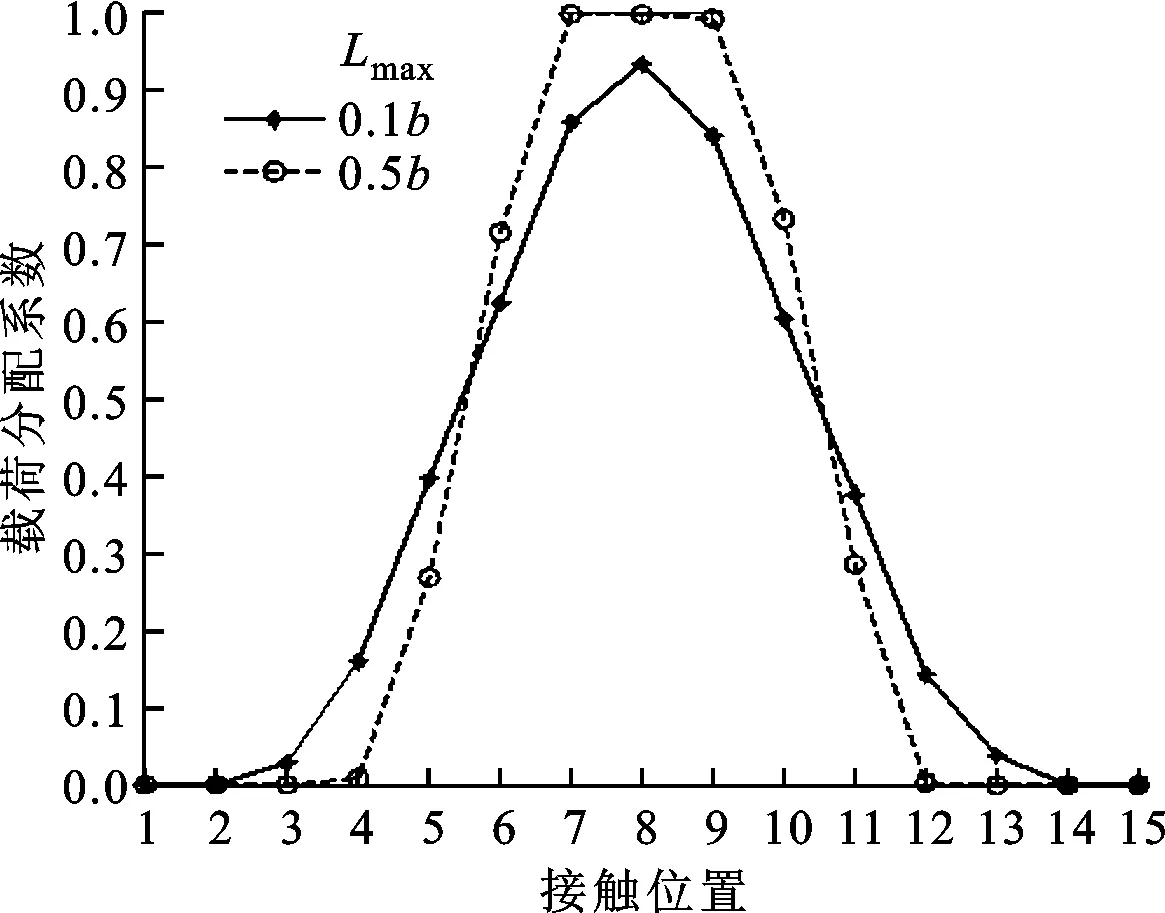
(b)载荷分配系数

(c)摩擦系数分配系数

(d)摩擦系数

(e)摩擦功率损耗图6 齿向修形斜齿轮的齿面摩擦情况
从图6a可以看出,齿向采用对称鼓形修形,两侧修形情况相同。从图6b可以看出,最大修形长度增大后,实际啮合点减少,中间啮合点载荷增大,而两侧啮合点载荷减小。从图6c可以看出,两侧摩擦系数分配系数为1,中间接触区域摩擦系数分配系数在0.74~0.87之间,以弹流润滑为主。从图6d可以看出,齿宽方向中心区域载荷大,摩擦系数较大。从图6e可以看出:当小轮转角为0、0.2φT、0.6φT和0.8φT时,最大修形长度大则功率损耗大;当小轮转角为0.4φT时,最大修形长度大则耗损功率小。这是因为当小轮转角为0.4φT时:在最大修形长度为0.1b情况下,啮合点3和13载荷较大,功率损耗较大;在最大修形长度为0.5b情况下,只有啮合点8实际啮合,虽然该点载荷大,但滑动速度很小,所以该位置功率耗损很小。综上所述,修形长度变化对功率损耗影响较大,齿向修形长度增大引起功率损耗波动较大,对传动不利。
4.3 拓扑修形斜齿轮的齿面摩擦功率损耗
取齿廓修形参数c=0.5 mm、R=250mn,齿向最大修形量25 μm,在最大修形长度为0.1b和0.5b2种条件下,对拓扑修形斜齿轮的齿面摩擦情况进行研究,结果如图7所示。

(a)拓扑修形量

(b)摩擦系数分配系数
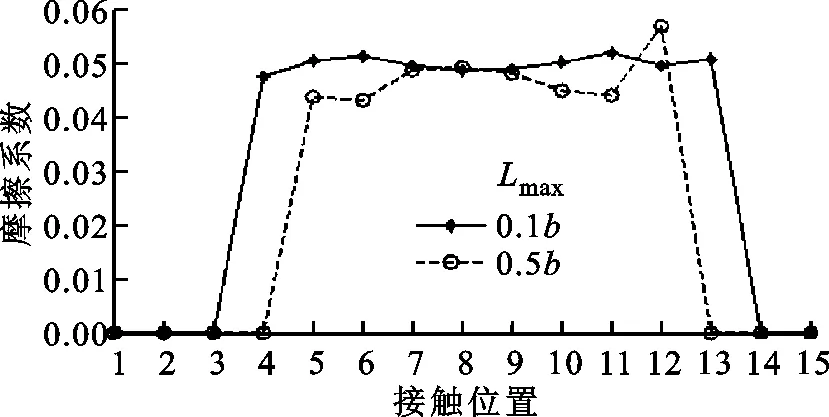
(c)摩擦系数
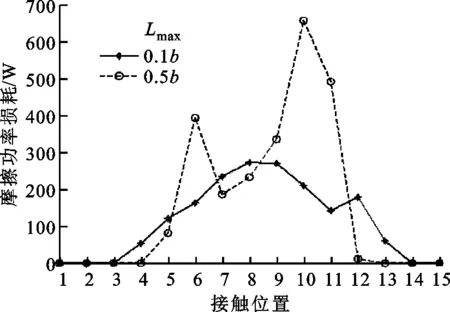
(d)啮合点对应的摩擦功率损耗

(e)小轮转角对应的摩擦功率损耗图7 拓扑修形斜齿轮的齿面摩擦情况
从图7a可以看出,齿顶修形量比齿根修形量大,对齿根弯曲强度影响小。从图7b可以看出,由于两侧未实际啮合的点摩擦系数分配系数为1,中间接触区域摩擦系数分配系数为在0.75~0.85之间,以弹流润滑为主。从图7c可以看出,两侧未实际啮合的点摩擦系数为0,齿宽方向中心区域载荷较大,因而摩擦系数较大。从图7d可以看出,由于齿宽中心区域载荷较大,齿面摩擦功率损耗也较大。当最大修形长度为0.5b时,在啮合点7出现波谷。这是由该处滑动速度很小造成的。结合图6e和图7e可以看出,当最大修形长度为0.5b时,与单纯齿向修形相比,拓扑修形引起的功率损耗波动较小,对传动有利。
5 结 论
(1)研究了斜齿轮的齿廓修形、齿向修形和拓扑修形方法,基于TCA和LTCA提出了修形斜齿轮齿面摩擦功率损耗及混合弹流润滑条件下修形斜齿轮摩擦系数计算方法,为修形斜齿轮齿面摩擦功率损耗分析奠定了基础。
(2)对斜齿轮的齿廓修形、齿向修形和拓扑修形的修形参数与摩擦损耗功率之间的关系进行了仿真。对于齿廓修形,修形量变化对功率损耗的影响较小,而且齿廓修形损耗功率波动较小,对传动有利。对于齿向修形,最大修形长度变化对功率损耗影响较大,而且最大齿向修形长度增大后损耗功率波动增大,对传动不利。与齿向修形相比,修形长度较大时,拓扑修形下功率损耗波动量减小,对传动有利。
(3)通过修形改变了啮合点的等效曲率半径,从而接触应力、啮合点速度、接触椭圆率等发生了变化,因此弹流润滑摩擦系数、摩擦系数分配系数、摩擦功率损耗也随之发生了变化。下一步将深入研究齿向修形曲线及参数,以便减少摩擦功率损耗波动。
