发动机推力对大展弦比机翼颤振边界的影响

2019-02-14聂雪媛余明亮钟培楠杨国伟

西安交通大学学报 2019年1期

聂雪媛,余明亮,钟培楠,杨国伟

(中国科学院力学研究所流固耦合系统力学重点实验室,100190,北京)

翼吊式发动机的气动布局在当前民用飞机中得到了广泛应用[1],但这种布局使得发动机和机体之间会存在干扰。在飞行过程中,发动机推力会改变机翼的稳定性,即使推力本身的大小不足以引起机翼的失稳,但其与气动载荷和机翼弹性运动的耦合作用仍会改变机翼的颤振边界。现代飞行器的设计越来越追求轻质,使得机翼结构的柔性日趋增大,机翼的变形加剧,发动机推力和质量效应对机翼颤振速度的影响更为显著。因此,研究发动机推力对柔性机翼稳定性的影响,对于飞行器的设计意义匪浅。

发动机的推力相对于机翼来说,属于横向载荷,具有典型的随动特征,会对结构的振动模态和频率产生重要影响。Como最早研究了在自由端施加的横向随动力对弹性悬臂梁弯扭稳定性的影响,得到了临界随动力的解析解[2]。Feldt等考虑了随动力加载点处的质量,探讨了在翼尖随动力作用下机翼的气动弹性稳定性问题,指出横向随动力对气动弹性系统具有不稳定作用,而增加集中质量可提高系统稳定性[3]。Hodge等以机翼的弯扭刚度比作为参数,分析了柔性机翼的颤振特性,但没有考虑外挂的质量[4]。Fazelzadeh等研究了发动机质量、推力及其作用位置等参数变化对颤振边界的影响,指出不可忽视外挂质量对颤振边界的影响[5]。此外,张健等在文献[5]的基础上,进一步讨论了机翼后掠角和上反角的影响[6];陈全龙等分析了推力大小和作用位置对颤振速度的影响,指出了发动机推力效应在颤振分析中的重要性[7];王钢林等研究了机翼在不同攻角下的定常气动力与发动机推力联合作用下结构的固有振动和颤振特性,结果表明发动机推力可能成为大型运输机机翼设计的限制因素[8]。

目前已有的考虑发动机推力对机翼气动弹性稳定性影响的研究中,结构建模多采用基于有限元的线性梁模型或Hodges几何精确完全本征梁模型[9],气动力主要通过Peters有限状态模型、Theodorsen气动模型或者面元法等进行计算。当前,计算流体力学(CFD)技术已经广泛应用于流固耦合力学问题的研究,CFD-CSD(计算结构动力学)方法已成为当前进行非线性气动弹性分析可信度最高的方法[10-11],而如何采用CFD-CSD耦合方法进行考虑发动机推力影响的气动弹性稳定性分析,国内外尚未见到相关报道。

本文发展了一种基于Simo几何精确梁模型和雷诺平均Navier-Stokes方程的气动力耦合计算方法。首先以文献[12]中的流固耦合算法标模——带柔性悬臂梁的方柱绕流为算例,验证了该方法的准确性;然后以大展弦比机翼为研究对象,采用横向随动力和集中质量模拟发动机推力和外挂质量,分析机翼的弯扭刚度比、外挂点安装位置、外挂质量、发动机推力等参数的变化对机翼稳定性的影响规律。

1 CFD-CSD耦合计算方法

数值计算方法采用气动结构耦合的时域分析方法,将流体控制方程和结构动力学方程相耦合,进行考虑结构弹性变形的气动弹性求解。流固耦合问题通常包括流场运动、结构动力学以及在两者交界面处的数据交换,其基本方程和边界条件可表示为

(1)

S(u)=E(Q,x)

(2)

x=H(u) onΓ

(3)

式(1)为流场控制方程,其中Q(x,t)是式(1)基于欧拉坐标的解向量,F和Fv分别是无黏和黏性通量;式(2)为结构动力学方程,其中u是结构节点位移,E是作用在结构节点上的外部气动载荷;式(3)描述了流固耦合界面的连续性条件,其中H是结构位移到流场位移的插值算子,Γ是流固耦合界面。

1.1 结构模型

Hodges几何精确本征梁[13]是当前研究梁的几何非线性效应常用的方法,该方法在梁的几何变形上没有采取任何近似,利用速度和应变独立描述结构状态。在理论推导方面同样没有采取任何近似的是Simo几何精确梁[14],它完全采用微分几何语言描述张量、截面转动和应变度量等物理量,具有明晰确定的几何意义[15]。考虑到Simo理论在数学描述上的优势,本文尝试采用基于Simo几何精确梁理论发展起来的几何精确梁模型对大展弦比机翼进行结构有限元建模,以期为当前梁结构的建模方法提供更多的选择。

该几何精确梁模型将结构的运动分为两部分,一是梁中心轴线的任意运动,一是梁横截面的有限转动,并以此来描述梁的任意大变形。梁在运动过程中除了受到弯曲、扭转和拉伸变形外,还受到剪切变形的作用。几何精确梁的示意图如图1所示。

图1 几何精确梁示意图

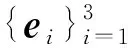
di=Λei

(4)

式中转动矩阵Λ满足ΛΛT=ΛTΛ=I3,|Λ|=1。

该模型的动力学方程可描述如下

(5)

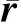
对动力平衡方程(5)不能直接使用有限元方法离散,需要通过虚功原理得到平衡方程的变分形式。对于给定的构型Φ=(φ,Λ)(φ为梁的轴线位置),允许的虚位移ζ=(η,ν),其中η为轴线的小位移,ν为横截面上的小转动。将这2个小量点乘式(5),并在梁的长度区间[0,L]上积分,最终得到

(6)

式中∂ΦΦ为Dirichlet边界,有

根据虚功类型不同,可将上式各项分为外力虚功Wext、内力虚功Wint及惯性虚功Wdyn,分别对应式(6)中各项,可写为

Wdyn+Wint=Wext

(7)

用一带集中质量Me的随动力来描述发动机对大展弦比机翼的推力,梁结构在随动力作用下需要考虑随动载荷对其模态带来的影响。

作用在梁结构某节点上的随动力可以表示为

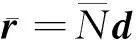
(8)

随动力的引入会改变结构的刚度矩阵,同时,随动力加载点处的附加质量也会改变结构的质量矩阵。通过推导随动力所做的虚功[16],可得作用在节点上的随动力切向载荷刚度

(9)

结构在外载荷作用下达到静平衡位置时,其切向刚度

(10)

设静平衡位置处的线化质量矩阵为MT,平衡位置处的模态振型φ和频率ω可以通过下式的广义特征值分析得到

(KT-ω2MT)φ=0

(11)

考虑发动机推力的结构平衡位置附近的小扰动动力学方程可写为

(12)

(13)

因此对式(13)在平衡位置进行线性化,可得

(14)

(15)

将其代入式(14)得

(16)

由于载荷刚度的加入,破坏了系统刚度矩阵的对称性,式(11)计算出的特征向量之间并不正交,所以不能在方程(16)左右简单乘以φT以转换为广义运动方程。将矩阵ψ作用于方程(16),该矩阵满足

(17)

式中1N为N阶单位矩阵,N为所取的结构模态阶次。求解矩阵ψ其实就是寻找MTφ的广义逆矩阵或伪逆矩阵,这可以通过奇异值分解的方法完成。最终得到结构的广义运动方程为

(18)

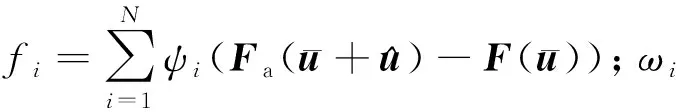
结构在不同随动力作用下的平衡构型不同,从而使得结构的模态也随之变化。因此,对于考虑发动机推力的机翼颤振计算,与线性颤振相比需要在结构静变形平衡位置计算结构的模态,属于非线性颤振计算。

综上所述,考虑发动机推力作用的机翼颤振计算流程如图2所示。

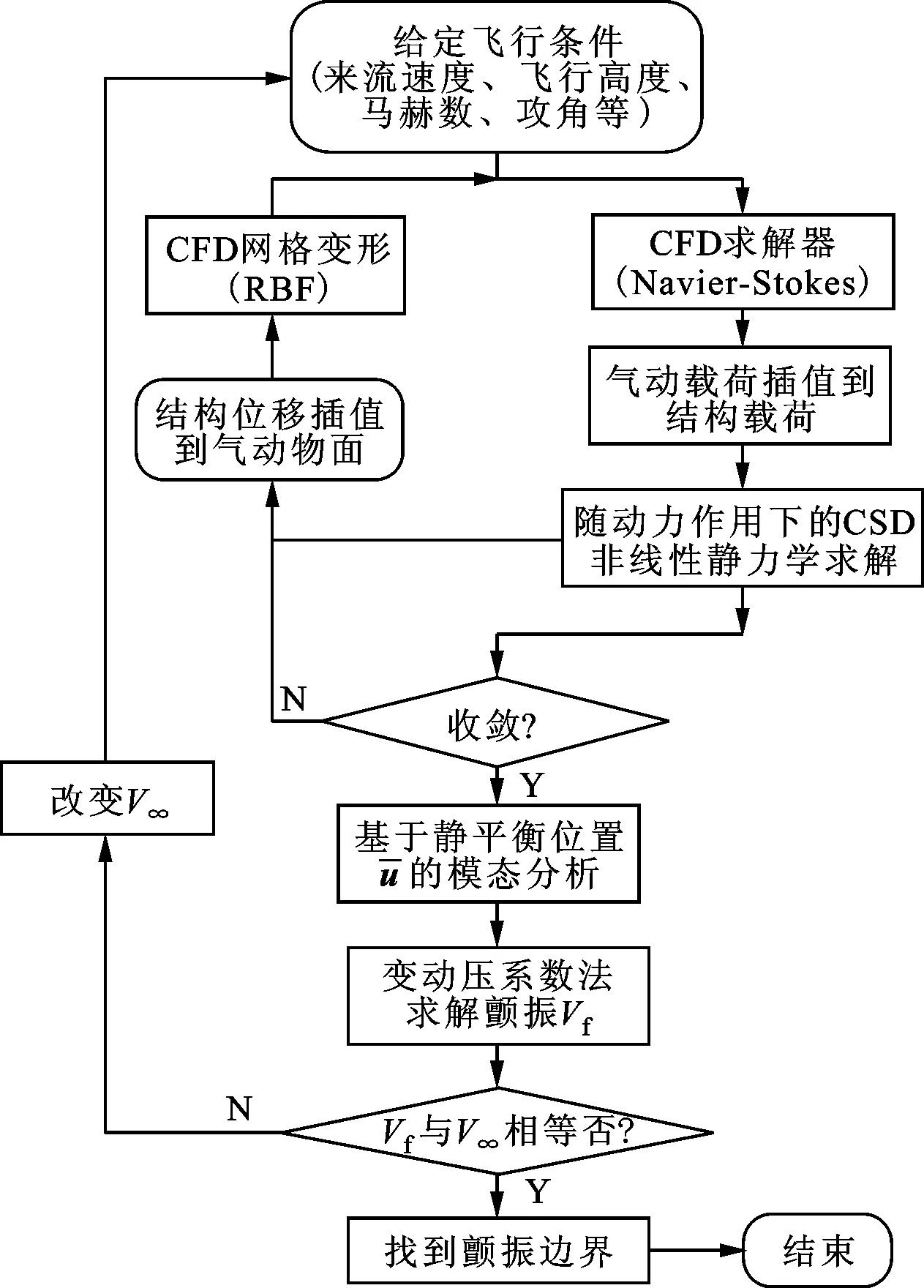
图2 CFD-CSD非线性颤振计算流程

1.2 气动控制方程

气动力数值计算软件采用自主开发的基于有限体积法的CFD求解器[17]。该求解器的控制方程为三维雷诺平均N-S控制方程。守恒型流动方程(1)的积分形式可表达为

(19)

式中:S为控制体V的边界面积;n为面的法向量;t为物理时间。将式(19)按有限体积法进行空间离散,可得

(20)

式中:VI为第I个控制体单元的体积;NF为包围第I个单元的所有面数;ΔSm为第m个表面的法向面积。

N-S方程组的空间离散分为无黏项和黏性项。黏性项的离散采用二阶中心差分格式。无黏项是非线性对流的集中体现,离散采用Roe格式,即

(21)

式中:A为Roe矩阵;上角标R、L分别表示相关变量来自单元界面的右边和左边。

对式(20)采用二阶三点近似,进行时间离散可得

(22)

式中RI为残差,代表式(20)的右边项。

为提高时间推进精度,在式(22)中引入虚拟时间,最终可得到以下时间离散形式

(23)

式中:上角标*表示虚拟时刻对应的物理量;l为虚拟时间步。在虚时间域上采用LU-SGS(lower-upper symmetric Gauss-Seidel)隐格式对气动方程作隐式时间推进,当子迭代步l→∞时,Q*l→Qn+1即可求得流场在下一物理时间步的解。

该CFD数值仿真软件已经在工程应用中得到了验证[1,17-19]。

1.3 气动-结构耦合

由于结构和气动控制方程在数学模型和求解方法上的不同,难以实现两者的统一求解,目前通用的方法是将结构和气动独立求解。由于在耦合界面上流场和结构网格具有不同的拓扑形式和分布密度,需要对2个子系统在界面上进行力和位移的交换。

用xf和us分别表示耦合界面上流场和结构网格的位移,λf和λs分别表示作用在界面上的流体载荷和结构载荷,耦合界面的运动必须满足的2个条件为

(24)

为了保证界面总能量守恒,在界面上的数据交换必须要满足虚功原理,即

(25)

式中δW为虚功。界面上流场网格点的位移可通过结构网格点的位移插值得到,即

xf=H·us

(26)

其中插值矩阵H由所采用的插值方法来确定,采用基于径向基函数(RBF)的插值方法[19],以实现流固耦合界面的数据交换。将式(26)代入式(25),可得由界面气动力载荷转换得到的结构节点力

λs=HT·λf

(27)

流固耦合的迭代过程如图3[20]所示。

图3 流固耦合计算的迭代过程

在计算得到流场结构交界面的气动物面位移之后,就可以调用动网格变形技术进行整个流场空间网格的变形。采用并行RBF插值方法进行空间网格变形,具体过程可参见文献[19]。

2 方法验证

为验证本文所采用的CFD耦合几何精确梁方法的正确性,对浸没在流场中带有柔性悬臂梁的方柱进行结构响应分析,并与已有文献的结果进行比较。该模型是验证流固耦合算法的标模,模型参数详见文献[12]。柔性悬臂梁选用几何精确梁作为结构模型,共用41个有限元节点离散,其计算流场如图4所示。

图4 带悬臂梁方柱的计算网格

流体经过方柱会产生涡脱落,引起柔性悬臂梁振动,其中自由端的振幅和振动频率是诸多文献作为判断求解流固耦合算法是否准确的关键参数。采用本文方法计算出的自由端垂向位移和振动频率如图5所示。

(a)自由端垂向位移时程

(b)自由端位移频谱图5 悬臂梁自由端垂向位移的计算结果

从图5可以看出,自由端垂向位移平均幅值为1.05 cm,其主频约为3.2 Hz。

表1给出了本文与已有文献的计算结果比较,

表1 计算结果比较

可以看出本文方法得到的结果与其他文献的结果吻合良好。

3 算例与分析

对本文方法进行验证后,以文献[4]中的大展弦比Hale机翼为研究对象,首先研究不考虑气动力时发动机推力对机翼稳定性的影响,具体分析发动机的安装位置、质量以及结构刚度比的作用,并在此基础上探讨上述各参数对大展弦比机翼气动弹性稳定性的影响规律。

Hale机翼模型的结构参数和飞行条件见表2,其中弦向弯曲刚度远大于展向弯曲刚度(EI3≫EI2),γ为展向弯曲刚度与扭转刚度之比。机翼采用梁模型描述,在发动机推力作用下的机翼示意图如图6所示。

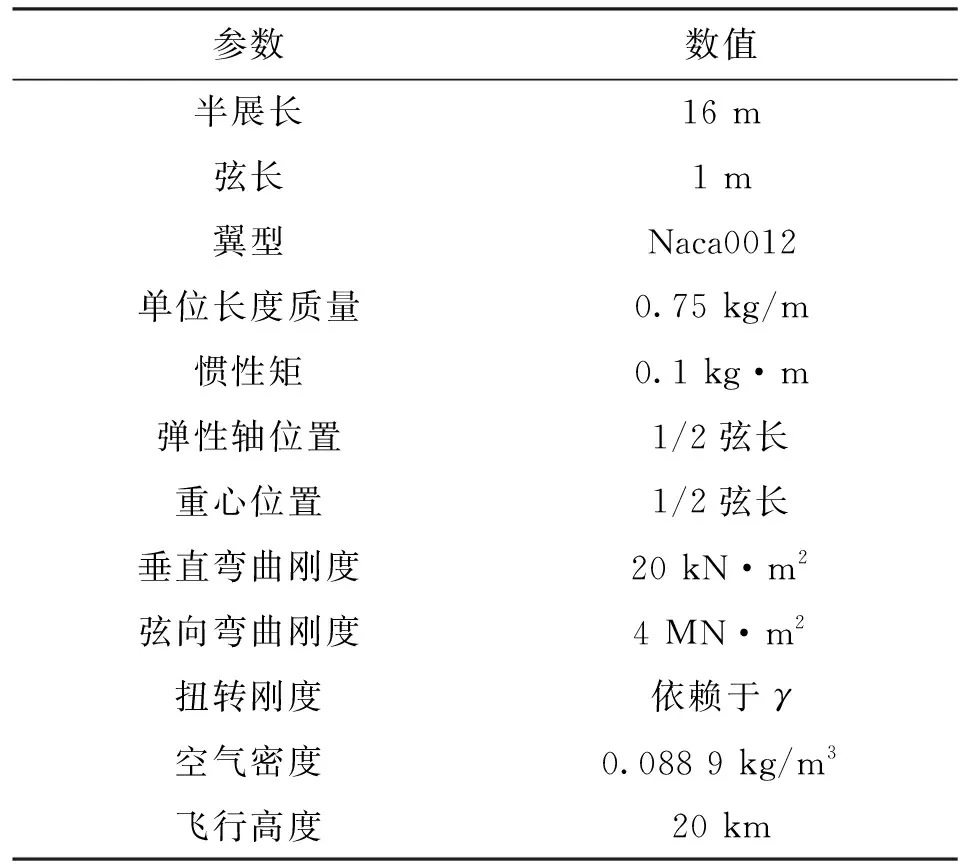
表2 Hale机翼模型的结构参数和飞行条件

图6 随动力作用下的Hale机翼梁模型示意图

采用本文1.1小节中基于Simo理论的几何精确梁模型建立机翼的有限元模型,y轴对应于机翼的弾性轴,即几何精确梁的中轴线,通过1/2弦长位置。采用30个有限单元进行计算;为进行界面耦合,在梁模型截面分布了6个离散点。图7是建立的机翼几何精确梁有限元模型,其中圆点代表有限元节点,正方形点代表用于流固耦合界面数据交换的结构网格点,亦即用于耦合界面进行位移和气动力插值的结构节点。

(a)有限元模型俯视图

(b)梁模型横截面图7 Hale机翼有限元模型定义归一化参数如下

(28)

式中:U为来流速度;ωT1为结构的第一阶固有扭转频率;Ye为发动机位置到机翼根部的展向距离;Xe为相对于弹性轴的集中质量弦向位置(位于弹性轴的后方为正);b为1/2弦长;c为机翼弦长;Ma为机翼质量;Me为发动机集中质量。下文各图中未标明单位的均为归一化数据。

流场计算网格采用混合网格,为更好地刻画边界层内的流动,在壁面附近布置了边界层网格。首层高度为机翼特征长度l的3×10-6倍,计算网格规模约为67万,流场计算网格如图8所示。湍流模型采用两方程涡黏性模型——Wilcoxk-ω模型。

图8 Hale流场计算网格

3.1 发动机推力对机翼结构模态的影响

3.1.1 发动机推力对结构模态的影响计算中采用的模态为结构的前5阶模态,包括4个弯曲模态和1个扭转模态。用Vi代表第i阶垂直弯曲模态,Hi代表第i阶水平弯曲模态,Ti代表第i阶扭转模态。

首先,对本文的几何精确梁模型进行方法验证。给定梁的弯扭刚度比γ=2,在翼梢(即ye=1处)施加横向随动力P,在结构静平衡位置处进行稳定性分析,即对式(11)进行特征值求解,得到系统的临界推力为332.6 N,与文献[4]中给出的335.1 N基本吻合,证明了基于Simo理论发展的几何精确梁模型求解方法的有效性。

图9给出了在γ=2、其他变参数为0的情况下,发动机临界推力P随发动机安装位置ye的变化曲线,从中可以看出,发动机安装点距离翼根越近,则其临界推力越大。

图9 γ=2时结构不同位置的临界推力

由于推力和结构的平衡位置均有所不同,使得系统质量矩阵和刚度矩阵发生改变,最终导致结构模态发生变化。

选定γ=2,ye=1,其他变参数为0,计算系统特征值(特征值的实部代表频率,虚部代表阻尼)随发动机推力的变化,结果如图10所示。

(a)机翼频率随推力的变化

(b)阻尼随推力的变化图10 γ=2、ye=1时系统特征值随推力的变化

(a)p=0,xe=0

从图10中可以看出:一阶水平弯曲频率H1不受推力的影响,其值基本保持不变;在临界推力范围内,一阶垂直弯曲频率V1和一阶扭转频率T1随着推力的增大而逐渐增大;二阶垂直弯曲频率V2和三阶垂直弯曲频率V3随着推力的增大而减小;当推力超过临界值(此处p=6.02)时,系统出现了复数特征值,一阶和二阶垂直弯曲对应的特征值最先形成一对共轭特征值,系统进入不稳定区域,该现象与文献[4]中的情况相似。

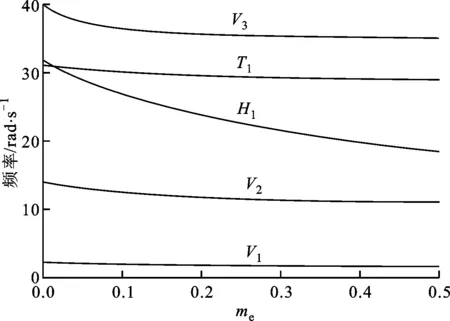
(b)p=0,xe=0.25图11 γ=2、ye=1时机翼特征频率随发动机集中质量的变化

3.1.2 发动机质量对结构模态的影响为研究发动机质量效应对结构的影响,选取γ=2,ye=1,改变发动机的集中质量,分别计算发动机安装在xe=0,0.25位置时,机翼的特征频率随发动机质量的变化,结果如图11所示。

从图11可以看出:当发动机安装位置位于机翼端部时,除一阶扭转频率T1外,结构各阶频率都随着集中质量的增大呈现出下降趋势;当发动机安装的弦向位置位于弹性轴,即xe=0时,质量对弹性轴无转动惯量,因此一阶扭转频率T1不受集中质量变化的影响,随着发动机弦向安装位置远离弹性轴,质量相对弹性轴产生转动惯量,此时一阶扭转频率T1随集中质量的增大而逐渐减小。此外,发动机安装在机翼弹性轴前后位置对结构模态的影响很小,这是因为在本算例中没有考虑气动载荷的影响,大展弦比机翼简化为一个梁模型,弹性轴前后对称,所以发动机前置或后置产生的差异并不大。

3.2 发动机推力对机翼气动弹性稳定性的影响

颤振是气动弹性领域中最危险的一类动不稳定现象。本小节从机翼颤振特性出发,研究发动机推力及其相关参数对结构气动弹性稳定性的影响。

与求解线性结构颤振不同,由于发动机推力随结构变形而变化的随动特性,机翼的模态发生改变,因此在分析机翼的颤振特性时,需要首先对建立在考虑随动载荷作用的静平衡位置上的线性小扰动结构动力学方程进行模态分析,即实现对方程(16)的广义模态求解。

3.2.1 发动机推力及作用的展向位置对颤振边界的影响给定γ=2,me=0,xe=0,研究机翼颤振特性随发动机推力及其作用在机翼不同展向位置的变化规律。展向位置ye=0.25,0.5,0.75,1处颤振边界随推力变化的计算结果如图12a所示;在归一化推力p=1,2,3,4时,机翼颤振速度随推力作用的展向位置的变化见图12b。

从图12a可以看出,发动机的位置越靠近机翼根部,推力对颤振特性的影响就越小,这是因为柔性机翼的稳定性依赖于其变形状态,而发动机推力作用越靠近翼根,其对机翼变形的影响就越小。此外,随发动机推力向翼根靠近,稳定效应的范围会不断增大,因此,应尽量将发动机安装在靠近机翼根部的位置。

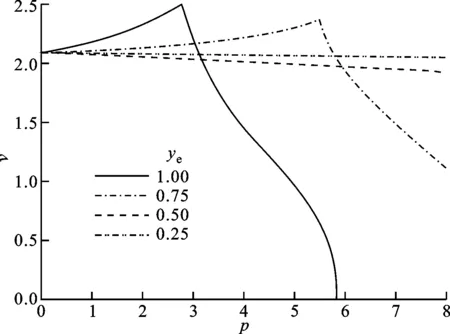
(a)推力对颤振速度的影响

图12b显示,在推力较小(p=1,2)时,发动机安装位置距离翼根越远,机翼的颤振速度就越大;随推力继续增大(p=3,4),颤振边界随展向位置的变化趋势发生改变,即随着p的增大,推力的增稳效应逐渐减弱,这是因为诱发结构失稳的推力和气动力耦合作用中所包含的不稳定效应增强的结果。

(b)展向位置对机翼颤振速度的影响图12 γ=2、me=0、xe=0时发动机推力和展向位置对机翼颤振速度的影响

注:发动机推力的增稳效应是指,随着发动机推力的增加,机翼颤振速度随之增大或基本保持不变的特性。

3.2.2 发动机的弦向位置对颤振边界的影响图13所示为γ=2、ye=1时,给定发动机集中质量条件下不同弦向位置对机翼颤振边界的影响。

(a)γ=2,ye=1,me=0.2

集中质量弦向位置的变化不会导致发动机推力关于弹性轴产生附加力矩,因此图13中各曲线之间的相互关系反映出集中质量的弦向位置变化对颤振特性的影响。从图13可以看出,随着集中质量从机翼后缘向前缘移动,颤振边界不断扩大,这是因为集中质量位于弹性轴之前有助于减小局部有效攻角,提高颤振速度。从图13a可以看出,当me=0.2时,集中质量前置(xe由0.25到-0.25)使得机翼颤振速度变化曲线的拐点向右上方移动,发动机推力增稳效应的范围增大。在图13b中,对于较大的质量me=0.4,发动机后置时颤振速度变化曲线的拐点消失,可见发动机推力增稳效应的范围也受集中质量弦向位置变化的影响。因此,安装发动机时应该考虑将发动机安装在机翼弹性轴之前,以提高系统的气动稳定性。

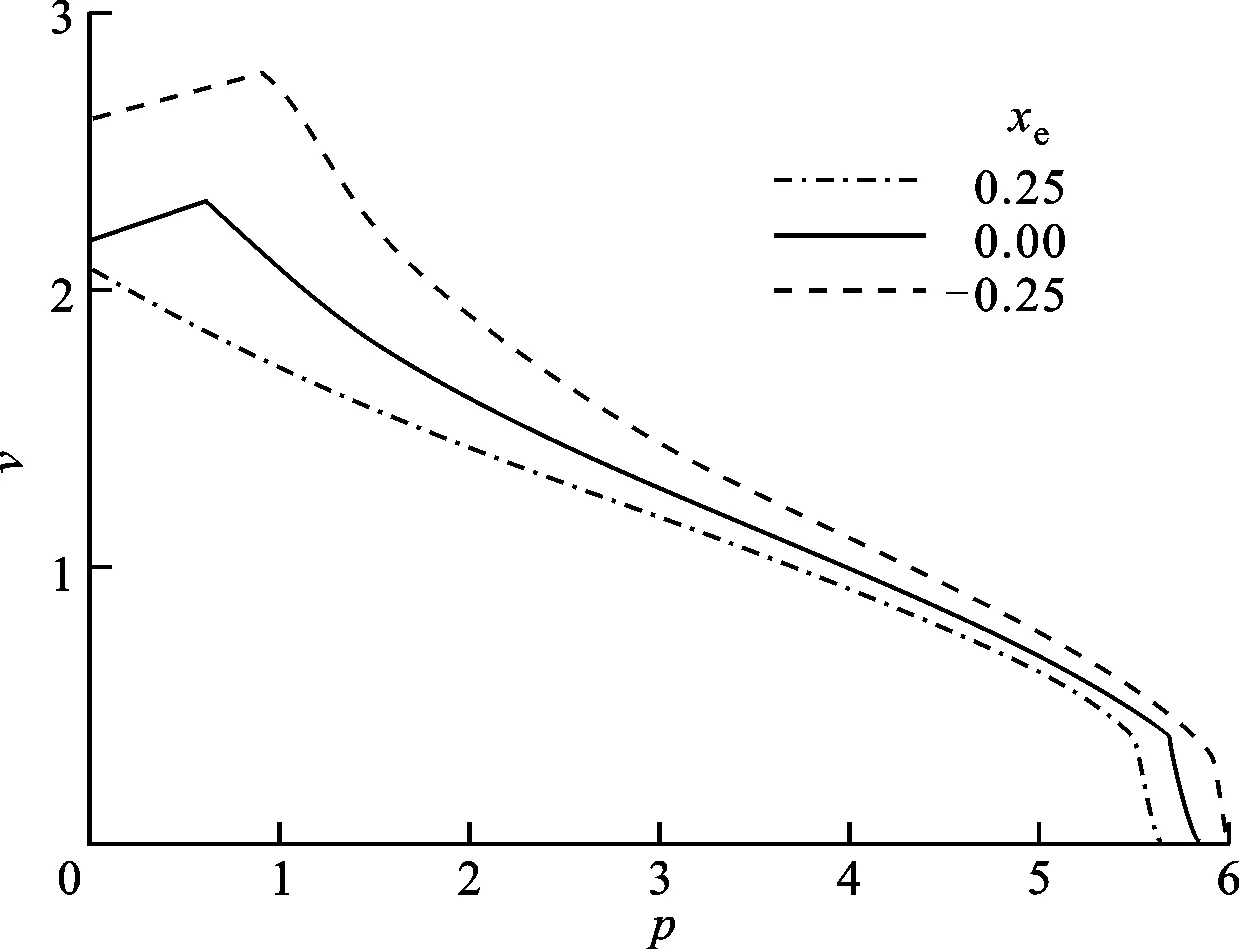
(b)γ=2,ye=1,me=0.4图13 集中质量的弦向位置对颤振边界的影响

3.2.3 发动机集中质量和推力对颤振边界的影响给定γ=2,ye=1,xe=0,研究发动机推力及集中质量对机翼颤振边界的影响。计算了当发动机归一化集中质量me=0.1,0.2,0.3,0.4时推力对颤振速度的影响(结果见图14a),以及归一化推力p=1,2,3,4时机翼颤振速度随集中质量的变化(结果见图14b)。

图14a的计算结果表明,柔性机翼的颤振速度以及发动机推力的稳定效应几乎不受集中质量变化的影响,随着发动机推力的增大,其增稳效应逐渐减弱,直至呈现出加速机翼失稳的作用(随着发动机推力增大,颤振速度快速下降),这与图12b的结果相似。

图14b的结果显示:随着发动机推力的增加,机翼颤振速度随集中质量的增大呈现下降趋势;集中质量增大会降低机翼的气动弹性稳定性,集中质量越大,机翼越容易发生颤振。

(a)颤振边界随推力的变化

3.2.4 弯扭刚度比对颤振边界的影响选取ye=1,γ=1,2,5,10,其他变参数为0,研究机翼颤振边界随推力的变化,结果如图15所示。

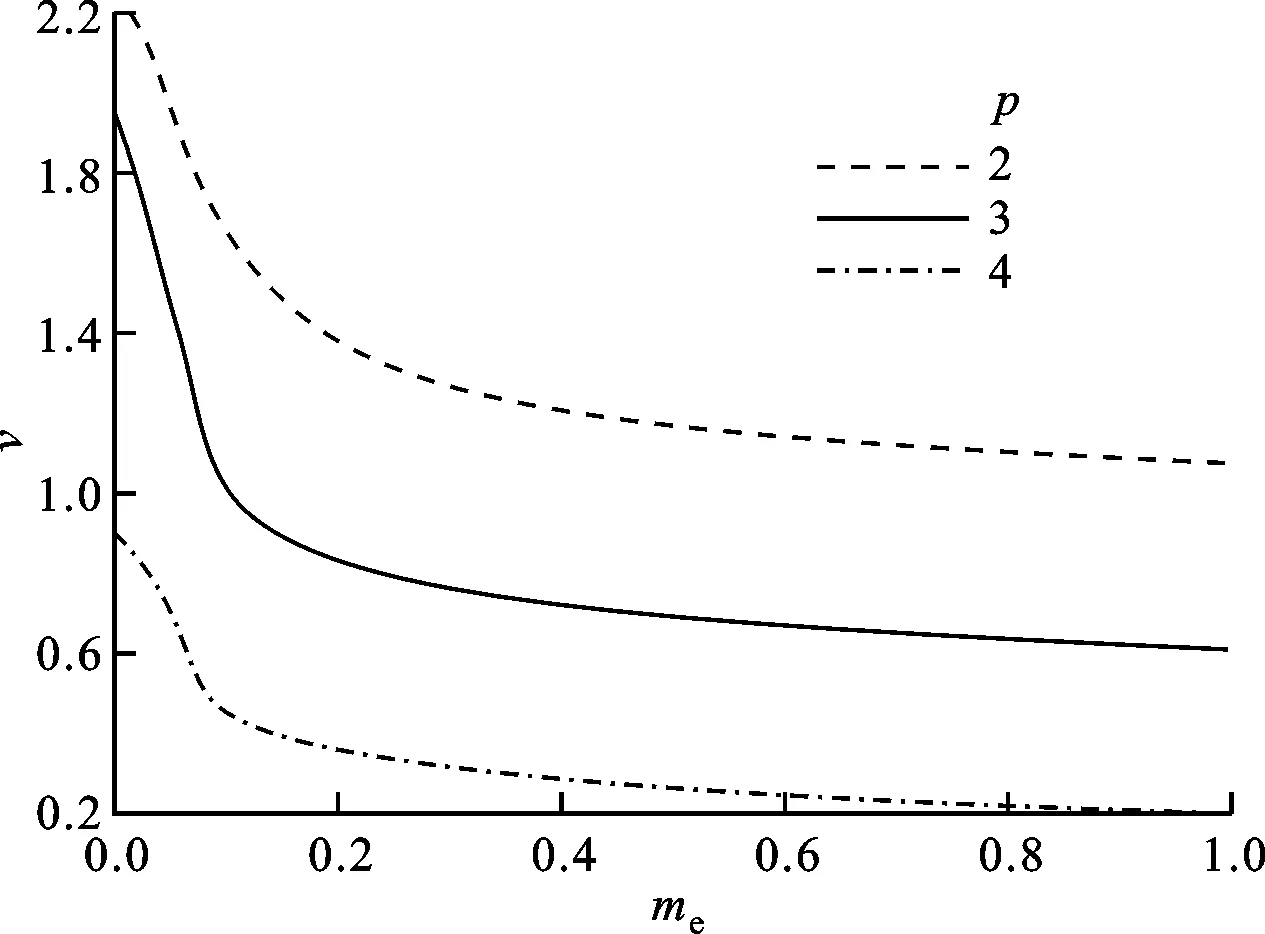
(b)颤振边界随集中质量的变化图14 γ=2、ye=1、xe=0时集中质量和推力对颤振边界的影响

图15 弯扭刚度比对颤振边界的影响

由图15可以看出,颤振速度随推力的变化趋势在γ=5时发生了改变,在这一刚度比下,尽管仍有颤振速度随推力增大而增大的发动机稳定效应范围,但是与γ<5时相比,颤振速度随推力变化的突变拐点不再存在,这是由于在该刚度比下,发动机推力和气动力中所包含的不稳定因素相互作用的机理发生了改变[4],导致不同弯扭刚度比值(γ=1,2,10)所对应的颤振包线变化趋势明显不同。