基于事件触发的海洋平台模糊H∞控制方法
2019-02-14熊佩雪张宝琳
熊佩雪,张宝琳
(中国计量大学 理学院,浙江 杭州 310018)
海洋平台作为海洋油气资源开发的基础性设施,长期处在海洋环境中不可避免地受到大风[1]、地震[2]等环境载荷的作用。这些外部载荷的作用可能导致海洋平台结构受损、寿命减少甚至威胁平台上工作人员的安全等。因此,研究海洋平台的结构振动控制方法来确保它的安全性和可靠性具有重要意义。海洋平台最常用的控制方法主要有三类:被动控制[3]、主动控制[4]和混合控制[5]。被动控制结构简单容易实现,半主动控制结合了被动控制和主动控制的特点,有良好的稳定性及较高的可靠性。然而,被动控制和混合控制往往具有性能较为单一、控制成本高、减振效果有限等局限性。主动控制方法通过在结构上添加主动控制装置实现主动减振确保结构系统的性能,其适应性较强,控制效果更优。因此,海洋平台的主动减振控制方法,例如鲁棒最优控制、滑模变结构控制、采样控制、模糊控制等方法的研究引起了学者们的重视[5-8]。
随着控制对象越来越复杂与分布区域日益扩大,传统点对点控制存在维护困难、维护成本高等局限性。因此,具有诸多优点的网络控制系统(Networked control system,NCSs)的理论和应用受到越来越多的关注。特别地,近年来,学者们提出并研究了基于网络化控制的海洋平台系统建模和主动减振控制问题[9-11]。注意到网络控制系统的控制器和执行器等系统组成部分通过通信网络联接,为有效地节约通信网络带宽资源,提高网络化控制系统的性能,研究基于事件触发的网络化控制系统分析与设计问题具有重要意义[12]。特别地,基于事件触发的海洋平台网络化主动减振控制方法研究值得深入研究。
本文研究基于事件触发的海洋平台模糊H∞主动减振控制方法。首先,针对受到外部波浪力扰动的具有主动质量阻尼器(Active mass damper,AMD)装置的导管架海洋平台,基于文献[8]给出的海洋平台T-S模糊模型,提出了一种基于事件触发的H∞模糊控制器设计方法,给出了海洋平台闭环系统渐近稳定的一个充分条件。最后,进行了数值仿真验证,仿真结果表明,本文提出的基于事件触发的海洋平台模糊H∞主动减振控制方法能有效减少平台在波浪力作用下的振动幅值,其减振效果优于已有的模糊状态反馈控制方法和滞后模糊状态反馈控制方法,而且所需要的控制力小,并能有效节约网络资源。
1 问题描述
为研究钢结构海洋平台在外部波浪力作用下的主动减振控制问题,本文考虑一类含有主动质量阻尼器(Active mass damper,AMD)的海洋平台简化模型,如图1所示。根据牛顿第二定律,考虑海洋平台主振动模态和AMD质量摄动的系统动力学方程可描述为:
(1)
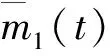
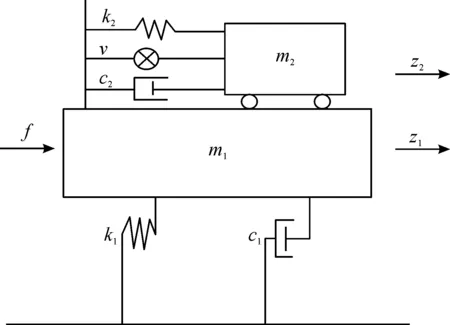
图1 海洋平台AMD模型[5]
令:
x1(t)=z1(t),x2(t)=z2(t),
xT(t)=[x1(t)x2(t)x3(t)x4(t)]。
于是,由式(1)可得海洋平台系统的状态空间模型为
x(0)=x0。
(2)
其中,
其中
设系统的输出方程为
z(t)=C1x(t)+E1f(t)。
(3)
其中
令
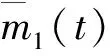
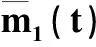
表1 模糊变量和的四种情形
注意到
(4)
显然,
进而,由式(2~4),容易得到海洋平台系统的模糊动力学模型如下:
模糊规则k:如果模糊变量为情形k,则
(5)

令

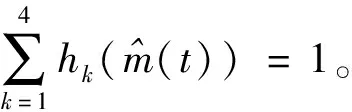
通过中心平均去模糊化方法,得到海洋平台系统的动态模糊方程为[8]:
(6)
为了得到本文主要结果,先给出下面引理。
引理1[11]设R为n×n常实矩阵,满足R=RT>0,ω:[a,b]→Rn。假设n×n矩阵Zi(i=1,2,…,6)和Lj,Tj(j=1,2,3),N1和N2满足
则下面不等式成立:
(v2+v3)T(T2-2N2)(v2+v3)。
进一步,令
i=1,2,…,6,j=1,2,3。
则有下面不等式:
其中
2 基于事件触发模糊H∞控制器设计

1)在采样时刻sh(s=1,2,…),如果下面事件触发条件成立,则释放当前数据包:
2)否则令s=s+1,转到步骤1)。

从事件生成器上释放的数据包通过通信网络被传输到控制器上,一旦控制器收到数据包(k,Py(kh)),控制器产生的控制信号数据包(ik,Yy(ikh))通过通信网络传输到零阶保持器进而驱动执行器,其中Y为待求的控制器增益矩阵。
为了设计基于事件触发的模糊H∞控制器,给出如下假设:
假设:所有的系统状态向量均是可测的,时滞τik有界,满足τm≤τik≤τM(k=1,2,…)。
考虑到零阶保持器的性质,控制律可写为
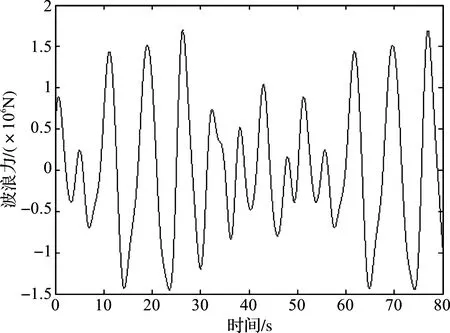
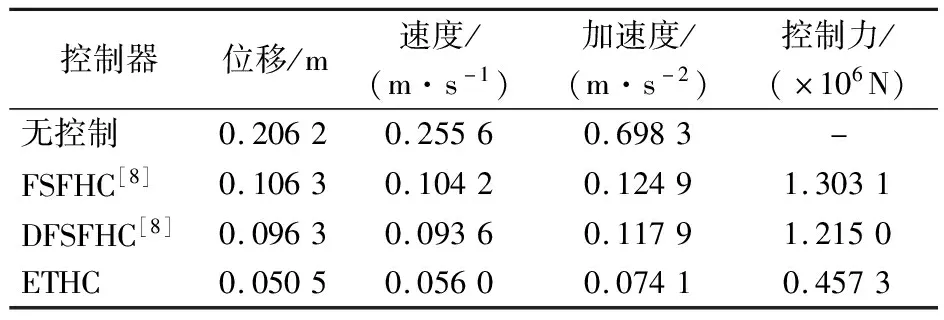
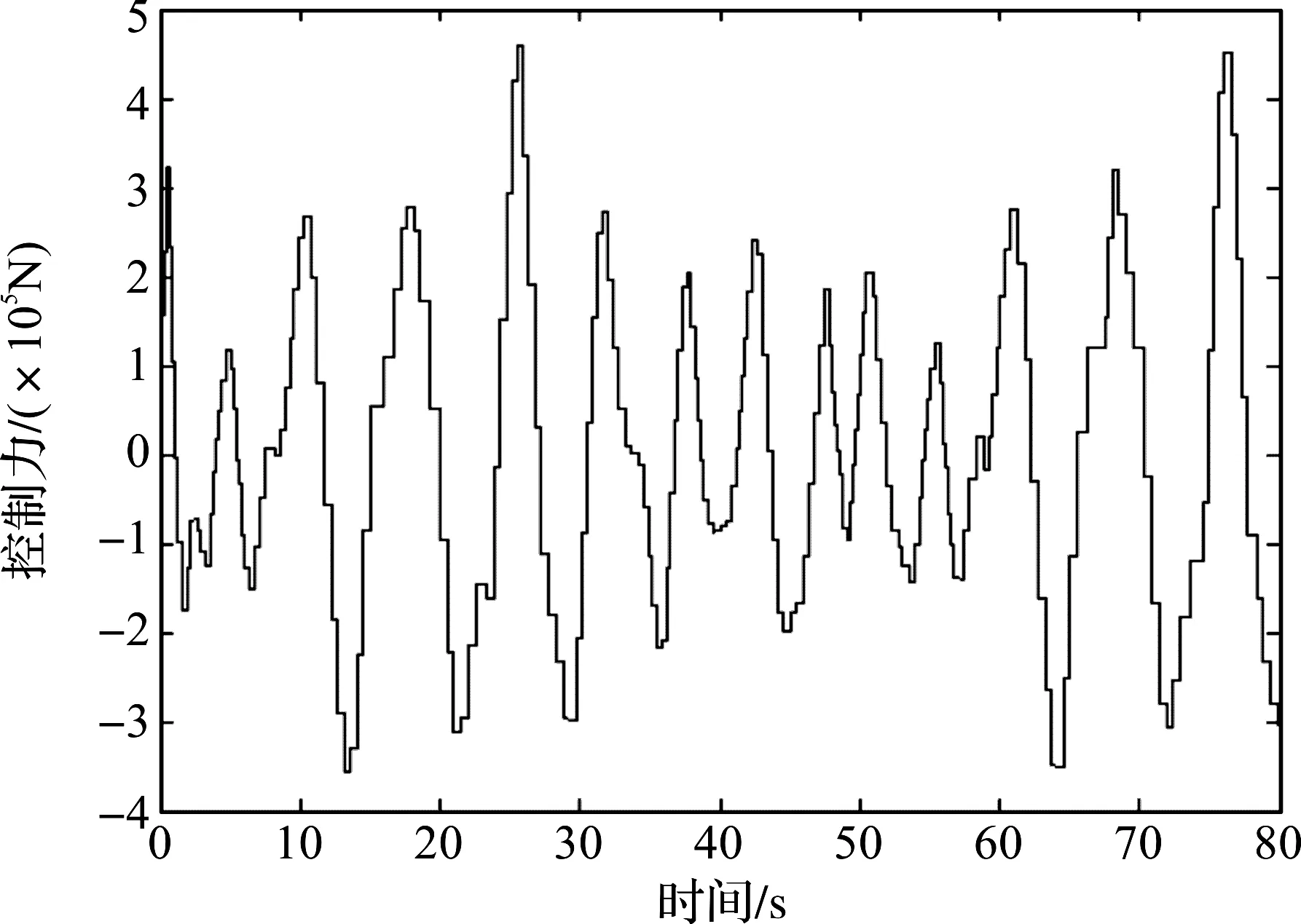
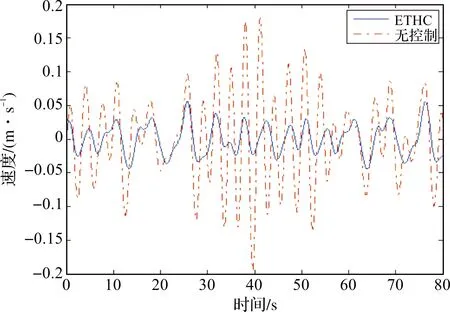
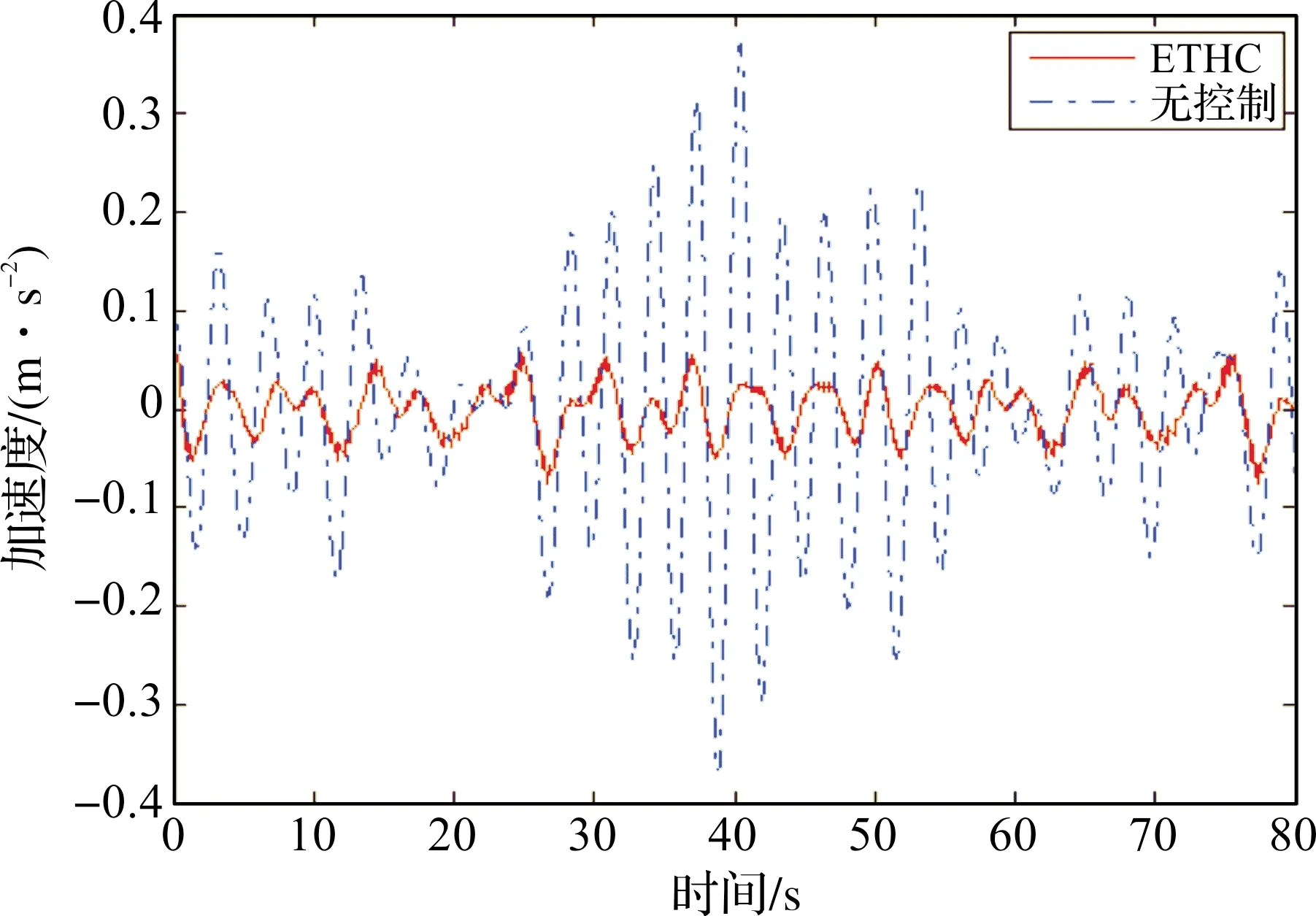
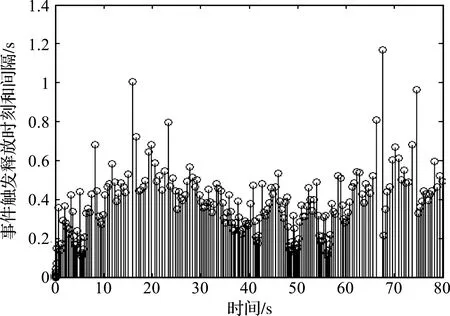
u(t)=Kx(ikh)=Yy(ikh),tk≤t 令lik=ik+1-ik-1,有[tk,tk+1)=Fik,0∪Fik,1∪…∪Fik,lik,其中 Fik,j=[(ik+j)h+τik+j,(ik+j+1)h+τik+j+1)。 令 τ(t)=t-(ik+j)h。 π(t)=y(ikh)-y(ikh+jh),t∈Fik,j。 则y(ikh)=π(t)+y(t-τ(t))。于是有 u(t)=Yy(ikh)=Y[π(t)+y(t-τ(t))],t∈Fik,j。 其中网络诱导时滞τ(t)满足: τ1≤τ(t)≤τ2。 其中τ1=τm,τ2=τM+h。 下面给出基于事件触发的H∞模糊控制器对应的模糊规则: 控制规则l:如果模糊变量为情形l,则 u(t)=Yly(ikh)=Yl[π(t)+y(t-τ(t))],t∈Fik,j。 其中,l=1,2,3,4,Yl是相应控制规则下的局部控制增益矩阵。进而,通过去模糊化可得到全局模糊控制律为 t∈Fik,j。 (7) 将基于事件触发的模糊H∞控制器(7)应用到海洋平台模糊系统(6),得到对应的闭环系统为: (8) 事实上,上述系统等价于: (9) 本文的目的在于设计模糊H∞控制器,使闭环系统(9)能满足以下条件: 1)在外部波浪力f(t)=0时,闭环系统是渐近稳定的; 2)在零初始条件下,闭环系统满足给定的H∞扰动抑制水平γ,即 ‖z(t)‖<γ‖f(t)‖。 (10) 对任意非零f(t)∈L2[0,∞]成立,这里γ>0为给定的标量。 为表示简单起见,令: l1=col{e1,e3,(τ2-τ(t))e7+(τ(t)-τ1)e6,τ1e5,τ1e8}, l2=col{e12,e11,e3-e4,e1-e3,e5-e3}, l3=e1+e3-2e5, l4=e1-e3-6e5+12e8, l5=e2+e4-2e7, l6=e2-e4-6e7+12e10, l7=e3+e2-2e6, l8=e3-e2-6e6+12e9。 其中,ei(i=1,2,…,10)是10n×10n单位矩阵的第i个n×10n块矩阵。 下面定理给出了海洋平台模糊H∞控制器的设计方法。 (11) (12) 则闭环系统(9)是渐近稳定的,且对于任意非零f(t)∈L2[0,∞],系统满足指定的H∞性能指标。其中 (13) 式(13)中 证明选取Lyapungov-Krasovskii泛函[13]如下: (14) 其中yt=y(t+θ),θ∈[-τ2,0],且: (15) 其中: 定义 其中: 根据(9)以及牛顿莱布尼兹公式,有 BY(y(t-τ(t)+π(t))-Df(t)]=0。 (16) 即 -2ξT(t)(e1+e12)T[(pe12- BY(e2+e13))ξ(t)-Df(t)]=0。 令 ζ(t)=[ξT(t)fT(t)]T。 (17) =2τ1[yT(t)ν1T(t)]Q1[yT(t) 0]T; 2(τ(t)-τ1)[yT(t)ν2T(t)]Q2[yT(t) 0]T+ 2(τ2-τ(t))[yT(t)ν3T(t)]Q2[yT(t) 0]T。 进而可得 (18) 其中 根据引理1,可得 从而,我们有 (19) (20) 下面,我们首先证明闭环系统(9)的渐近稳定性。为此,假设f(t)≡0。于是,由(17~20),容易得到 (21) 如果下列不等式成立 (22) 则对于τ(t)∈[τ1,τ2],有 下面证明在初始条件下,如果不等式(12)成立,对于任意非零项f(t)∈L2[0,∞),zT(t)z(t)<γ2fT(t)f(t)成立。 根据式(9),输出方程z(t)可写为 z(t)=Γζ(t),Γ=[C1Pe1D1]。 (23) 由式(20)和(23)可得 (24) 其中 运用Schur补和凸组合性质,有 ⟺ψ(τi)<0,i=1,2。 因此,如果不等式(12)和(13)满足,则ψ(τ(t))<0成立,进而ψ(τi)<0也成立。 由(24)式,可得 (25) 对(25)式两边同时关于t在Fik,j上积分,并将j从0加到lik,可得 令t0=0,将上述不等式关于k从0加到∞,结合零初始条件,有 即‖z(t)‖<γ‖f(t)‖。定理证毕。 (26) 图2 作用在海洋平台上的外部波浪力 假设网络诱导时滞是时变的,且在τm=0.01与τM=0.07之间变化。令事件触发参数σ=0.2,H∞性能指标γ=15。根据定理1,可以计算得到事件触发参数Ω和增益矩阵K分别为: Ω=103× 得到的基于事件触发的模糊H∞控制器,记为ETHC。当设计的ETFHC应用到上述海洋平台时,主动控制力的曲线以及海洋平台的位移、速度及加速度响应曲线分别由图3~6给出。表2给出了海洋平台在无控制情形、传统的模糊状态反馈H∞控制器(FSFHC)[8]、滞后模糊状态反馈H∞控制器(DFSFHC)[8],以及ETHC作用下的海洋平台位移、速度、加速度以及主动控制力响应的最大幅值。可以计算得到,在基于事件触发的H∞模糊控制器作用下海洋平台的位移、速度和加速度响应的最大幅值分别为0.050 5 m,0.056 0 m/s和0.074 1 m/s2,所需要的最大控制力为4.573 1×105N。同时,可以得到,在该控制器作用下海洋平台系统位移、速度和加速度的均方根值分别为0.023 9 m,0.022 4 m/s和0.026 0 m/s2,控制力的均方根值1.800 0×105N。显然,和FSFHC[8]、DFSFHC[8]相比,本文提出的模糊控制器ETFHC对减小海洋平台在波浪力作用下的振动幅值具有更好的效果,而且控制力更小。 表2 海洋平台在不同控制器下的位移、速度、加速度和控制力的响应值 Table 2 Maximum values of displacement, velocity, acceleration and control force of offshore platform under different controllers 控制器位移/m速度/(m·s-1)加速度/(m·s-2)控制力/(×106N)无控制0.20620.25560.6983-FSFHC[8]0.10630.10420.12491.3031DFSFHC[8]0.09630.09360.11791.2150ETHC0.05050.05600.07410.4573 图3 控制力响应曲线 图7给出了控制器执行过程中,事件触发信号的释放时刻与间隔信息。事实上,由计算知,采样数据包的传输率为2.84%,这表明在控制过程中只有2.84%的数据包通过通信网络传输,亦即,97.16%的网络资源得到了节省,这表明所设计的控制器在保证系统性能的同时还能够减少网络资源。 图4 海洋平台位移响应曲线 图5 海洋平台速度响应曲线 图6 海洋平台加速度响应曲线 图7 事件触发信号释放时刻与间隔 本文针对受到外部波浪力作用的含AMD结构的海洋平台,基于考虑平台质量和AMD质量的参数摄动建立的系统的T-S模糊动力学模型,根据李雅普诺夫泛函方法并采用积分不等式方法得到了海洋平台模糊系统稳定性的一个充分性条件,给出了海洋平台系统基于事件触发的模糊H∞控制器设计方法。仿真结果表明,本文提出的基于事件触发的模糊H∞控制方法能以更小的控制力达到更好的减振效果,同时能有效地节省网络资源。 DOI:10.1016/j.oceaneng.2019.106392.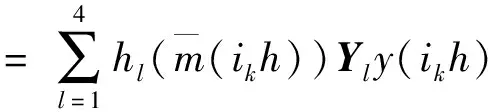

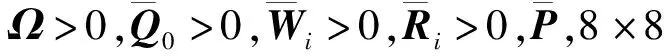
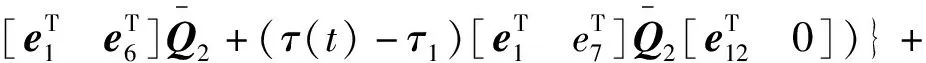




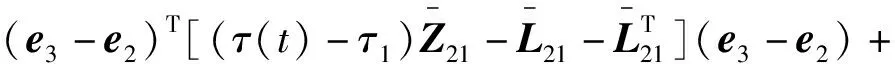

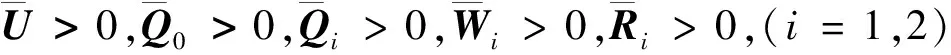












3 数值仿真

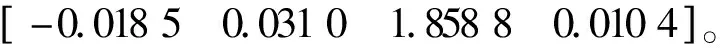

4 结 论
