卷积神经网络的压缩研究

姜懿家

（大连市第十三中学，辽宁大连，116000）

0 引言

近年来，卷积神经网络在语音识别，计算机视觉，目标检测以及制药、基因等领域取得了出类拔萃的效果。如图1所示，卷积神经网络[1]通过多个层次的特征学习，建立从底层特征到高级抽象特征的映射，使复杂的特征提取工作简单化，抽象化。这种比传统方法更符合人脑视觉机制的技术使深度学习能够学习到目标的一些隐形规律和规则，具有学习速度快，耗时小，识别率高的优点。

卷积神经网络规模庞大，消耗高昂的存储代价、能耗以及计算开销，严重制约了深度学习在嵌入式移动设备上的部署。同时卷积神经网络参数存在大量冗余，研究表明只需要训练完成后的一小部分参数[2]就可以保证深度网络的识别精度，这启发了卷积神经网络的压缩研究。有效的压缩方法提高了深度学习在分布式系统，嵌入式设备，FPGA等终端上的计算效率；比如，ResNet-50网络[3]拥有50层卷积计算，占用超过96MB的存储，大量的浮点乘法需要计算，如果舍弃冗余的参数，可以节约75%的存储空间和50%的计算代价。

本文介绍四种常用的卷积神经网络压缩方法：低秩近似[4]，剪枝与稀疏约束[5]，参数量化[6]，二值网络[7]。低秩近似是使用近似算法将大的矩阵乘法转为几个小的矩阵乘法计算，适合小规模网络及全连接层计算；剪枝与稀疏约束利用卷积神经了的参数冗余性移除掉不重要的神经元，是一种有效的通用压缩技术，但是训练比较复杂；参数量化使用码表代替原有权重，极大地降低了存储开销；二值网络是将权重量化到+1，能到最大限度地压缩网络，但性能损失也最为严重。

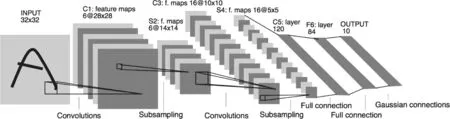
图1 卷积神经网络

1 低秩近似

卷积操作是深度神经网络的主要计算开销，因此减少卷积计算能够提高网络的压缩比率。例如，给定权重矩阵W ∈ Rm×n,若能将其表示为若干个低秩矩阵的组合，即，其中 Mi∈ Rm×n为低秩矩阵，其秩为ri，并满足ri<

低秩近似算法在卷积神经网络中取得了很好的压缩和加速效果。但是，矩阵分解是逐层计算，计算量较大；同时低秩近似修改了网络的原有结构，需要微调（ fi netune）网络。

2 剪枝与稀疏约束

由于训练后的卷积神经网络存在过参数化，通过剪枝去掉冗余的神经元，能够大幅压缩模型，同时提高网络的抗过拟合能力。比如，论文[9]提出无效数据剪枝方法来去掉冗余的神经元，论文[10]提出哈希网络模型利用哈希代价函数将权重映射到共享参数哈希表。于此同时，利用稀疏约束来对网络进行剪枝保证了神经网络的结构性。论文[5]在网络训练中引入稀疏正则项，使网络的部分卷积核权重趋向0，并剪枝这部分0值权重，这样保证了网络的结构性，同时只需要重训练一遍就能达到剪枝的目的。

在保持网络分类精度不下降的情况下，剪枝可以将网络参数压缩9～11倍。比如，在论文[5]将AlexNet网络的6千万参数量压缩到7百万，将VGG-16网络的1亿4千万参数量压缩到1千万，同时没有精度的损失。

总的来说，剪枝作为通用的压缩方法，能够应用到广泛的神经网络模型中，压缩率高同时精度损失很小。但是，剪枝特别是稀疏约束下的剪枝对网络的重训练要求较高，如何衡量神经元的重要程度以及是否剪枝是训练的关键。

3 参数量化

参数量化通过减少参数的比特数来达到压缩原始网络的目的。其中最简单的一种量化算法是标量量化[11]，该算法首先将权重矩阵转为标量形式，然后应用k-means算法对权重进行聚类。最后，只需要将k个标量存储在码表中，原始的权重矩阵只需要记录对应码表中的索引值。这样原始的浮点参数可以压缩为几个比特的索引值，能够将存储空间减少为原来的log2(k)/32,将原始网络模型压缩8～16倍。不过，当压缩率较高时，精度损失较为严重。

为了解决标量量化的精度损失问题，更加通用的结构化量化技术受到关注。其中QCNN[12]基于乘积量化方法，最小化每一层网络输出的重构误差，以此大幅压缩网络规模并保证了很小的精度损失。比如，QCNN将VGG-16网络的浮点参数减少4倍，规模减少20倍，同时精度只损失0.58%。

参数量化作为一种通用的压缩方法被广泛应用到FPGA,神经网络加速芯片，嵌入式设备中。其较高的压缩率和较低的性能损失使参数量化技术受到广泛关注，但是每一种参数量化方法需要专门的运算库来执行。无法应用到通用的卷积神经网络计算框架中（Caあe, TensorFlow等）,对于硬件也需要定制专门的计算单元来完成。

4 二值网络

由参数量化方法可知，降低参数的比特数是一种简单有效的压缩方法。如果将网络的参数压缩到1比特+1就能最大化压缩参数，这就是二值网络。二值网络可以分为三种类型：权重二值化，数据二值化，中间计算结果二值化。如果权重，数据及中间计算结果都二值化，那么网络的压缩率即最大，但这种方法目前不可实现，因为网络的精度会完全丢失。

常用的二值化方法是权重二值化，数据保持8～32比特。网络二值化的关键问题是如何训练二值化后的网络，因为网络大多基于梯度下降来反向训练参数。由于权重二值化，梯度将不能被计算。基于此，二值连接算法（binary connect[13]）采用单精度与二值相结合的方式来训练二值神经网络：网络采用二值计算前向过程，使用单精度权重进行反向的权重更新，从而加快网络的收敛过程。

同时如果在卷积计算中加入单精度缩放因子，可以有效降低网络的重构误差，实现在ImageNet数据集上与Alex-Net一样的精度。同时如果二值化数据，网络压缩率能进一步提高，但精度会下降12.6%。

5 总结

本文详细介绍了四种常用的卷积神经网络压缩技术：低秩近似，剪枝与稀疏压缩，参数量化，二值网络。如表1所示，低秩近似在全连接层应用最多，使用SVD可以压缩5～13倍；剪枝与稀疏压缩有效利用了卷积神经网络的过参数化特性，去掉冗余的神经元，能够减少大量权重，同时还可以增强网络的抗过拟合能力；参数量化方法是目前在FPGA和专用的硬件加速器中使用最普遍的方法，在不改变原始网络结构的基础上能够很好地压缩网络，节省大量存储空间；二值网络是压缩比最高的方法，但网络训练困难，精度损失大，二值网络是目前压缩研究的热点问题。卷积神经网络的压缩研究未来会集中在通用化、网络改动小、压缩比高、精度损失小等综合性能突出的压缩方法上，或者融合多种压缩方法应用到一个网络上，以最大化性能提升。

表1 网络压缩方法总结