混合驱动连续型机器人设计
2019-02-13康荣杰孙慈晶
康荣杰,孙慈晶
(天津大学机构理论与装备设计教育部重点实验室,天津 300350)
近年来随着机器人技术的发展,机器人已不仅用于工业生产在结构化环境中做重复性强的机械式工作,还拓展应用到了各种复杂的工况环境,比如灾难搜救、科学探测和微创手术等[1].在这些场景中,传统刚性机器人由于自由度和柔顺性不足,较难适应非结构化的环境,而兼具灵活性、多自由度、自适应性强的连续型机器人得到了施展空间,它的柔性本质更加适合人机环境共融的需求[2].
目前国内外已开展了许多关于连续型机器人的研究,比如意大利比萨圣安娜大学的 Menciassi等[3]设计了一种形状记忆合金(SMA)驱动仿蠕虫的爬行机器人.瑞士联邦理工学院的Shintake等[4]提出了一种电活性聚合物(EAP)制成的软体手.美国克莱姆森大学的 Walker等[5]开创了一系列气体驱动的连续型机器人.天津大学的 Kang等[6]也提出了一种采用可伸长的气动人工肌肉(PAM)组成的多关节连续型机器人.意大利圣安娜大学的Calisti等[7]研制了一种线驱动的连续型机器人.美国哥伦比亚大学的 Xu等[8]则采用 Ni-Ti拥有更高刚度的弹性杆来驱动机器人.通过电流直接驱动的SMA易于控制但是需要冷却时间,适合于低频的运动.同是电流控制的 EAP驱动器具备轻量化的优点,然而输出位移和输出力相对较小.气压驱动器可以产生大范围运动和较大输出力,但是欠缺一些精度.拥有很高的分辨率的线驱动仅能传递拉力,对于压力和侧向力的抵抗能力不足.换取了刚度的弹性杆驱动器则是以牺牲了一定程度的柔顺性为代价.回顾以上这些设计,可以看出单一的驱动方式难以兼顾精度、工作空间和输出力等各方面的性能.
为了提高机器人的综合性能,一种简捷有效的方法是采用混合驱动方式.Kang等[9]提出了一种内嵌驱动线的气动肌肉组成的连续型机器人.这种设计由气动肌肉主导输出力和大范围运动,内嵌的尼龙线提供额外精确的位置调整.然而由于驱动线过于柔软只能承受拉力,进行拉拽调整,而无法承受推力,限制了机器人精度的进一步提高.其他混合驱动器则关注变刚度的设计,目的是使机器人在穿越复杂的结构化环境时保持柔顺性,而在此之后自身刚度增强以便于进行精确的操作.康奈尔大学的 Brown等[10]创新性地提出了一种颗粒阻塞技术变刚度机械手,通过改变颗粒之间的摩擦力控制刚度.在此基础上,香港大学的 Li等[11]进一步提出被动颗粒阻塞的方法,简化了变刚度结构,然而这种颗粒阻塞的变刚度机构会增加机器人的尺寸和质量.国王学院的Shiva等[12]提出了一种基于拮抗原理的连续型机器人,利用气腔的伸长力与驱动线的拉力对抗来增加内力以达到变刚度的目的,但是它的刚度与姿态的控制是耦合的.
本文的目的在于提出一种兼顾各方面性能的机器人设计,综合考虑精度、柔性、工作空间大小等性能.正如上文所提到的,气动肌肉能提供大范围的运动,而弹性杆在不失柔性的基础上,相比尼龙丝线具有高的刚度(尤其是轴向刚度).笔者在本文的设计中结合二者的优势,将弹性杆嵌入到气动肌肉当中,形成一种新型的同心结构混合驱动器.运动时,气动肌肉提供快速的大范围运动,并且这个过程中机器人的柔顺性较高.到达指定工作位置附近时,由弹性杆驱动机器人进行精确定位,此时机器人刚度较高.本文还将分析机器人的静力学模型,建立输入气压与机器人构型的关系,并通过实验验证.
1 混合驱动机器人机械结构设计
在大自然中,章鱼的触手是一个典型的连续型结构.它的内部没有骨骼,而是靠内部并联的纵向肌和横向肌结构使它能够伸缩以及朝任意方向进行弯曲[13].本文的连续型机器人借鉴这种肌肉组织形式,并进行工程优化.通过并联布置 3组可伸长的驱动器,以实现机器人的弯曲和伸缩控制.由于连续型机器人形体细长、径向空间有限、侧向刚度较低、难以保持形状,因此本文提出一种气动肌肉内置弹性杆的创新设计以提高系统紧凑性和刚度.混合驱动机器人是由机械臂和驱动平台两部分组成,图1展示了机器人的整体结构.机械臂由 3个混合驱动器(以下简称驱动器)以及上、中、下 3个白色的连接盘组成.3个驱动器的轴向运动能使操作臂向任意方向弯曲和沿操作臂轴向伸长,连接盘使驱动器在任意姿态都能保持互相平行.
驱动器的结构如图 1所示,它由尼龙编织网套、橡胶管、弹性杆和气动接头等组成.在充入高压气体时,最外层的编织网套限制驱动器径向膨胀而只允许驱动器沿轴向伸长[14].弹性杆为 NiTi合金材料,具有超弹性,它起到驱动器的结构支撑作用,它的顶端与气动肌肉的顶端固连在一起,向下穿过气动接头到达驱动平台.笔者在弹性杆上布置了 5个限制模块用来使弹性杆始终处于气动肌肉的中心线位置,在气动接头里面布置了橡胶垫防止气体泄漏.机器人使用薄膜传感器(sparkfun)来测量弹性杆的位移,如图2所示,红色的传感器触头固定在弹性杆上沿着蓝色的导轨上下移动,这个位移也就是驱动器长度的变化量.表1列出了驱动器的具体几何参数.

图1 混合驱动机器人整体视图和驱动器结构Fig.1 Overall view of the hybrid-driven robot and the actuator structure

图2 传感器布置示意Fig.2 Schematic diagram of the potentiometer arrangement

表1 驱动器几何参数Tab.1 Geometrical parameters of the actuator
驱动器具有气压驱动和电机驱动两种工作模式.在气压驱动模式下,驱动器等同于气动肌肉,拥有较大的工作空间.而在电机驱动模式下,使用直线电机(Haydon,0.003175mm/步,4kg 推力)在竖直方向推拉弹性杆对驱动器进行控制,能够实现小范围的精确定位调整.机器人根据弹性杆是否与直线电机锁紧来区分驱动模式,驱动模式切换机构如图 3所示.锁紧弹性杆时,舵机驱动椭圆形凸轮旋转,由 3D打印的基座与凸轮从侧面共同夹紧弹性杆,从而将直线运动由电机传递到弹性杆.凸轮反转一定的角度即可松开弹性杆,使驱动器进入气压驱动模式.弹性杆的表面覆盖了一层硅胶套用以增加摩擦力防止夹紧时产生打滑现象.

图3 驱动模式切换机构Fig.3 Structure of the drive mode switching mechanism
2 控制系统设计
混合驱动系统的控制结构如图 4所示.每一个驱动器都是根据选定的驱动模式由电机或电气比例阀独立控制.使用 PC作为上位机,与单片机DSP(TMS320F28335)通过 RS-232进行串口通讯.由上位机发送期望的驱动器长度,由 DSP来控制电气比例阀(SMC ITV1051)、直线电机、舵机(EMAX ES08MAII)以及读取传感器回传的数据.

图4 控制结构Fig.4 Control architecture
混合驱动器的控制逻辑如图 5所示.当接收到期望长度信息时,首先需要传感器检测驱动器的实际长度并且与目标长度做比较.当实际与期望的误差大于设定阈值时,机器人对驱动器进行气压驱动,粗略地调整驱动器的长度.当误差等于或小于设定阈值时,保持气压不变同时舵机旋转夹紧弹性杆,切换至电机驱动模式,进行长度的精细调节.在这个控制过程中,如将阈值设定得太大,系统将过早地切换至电机驱动,这样会降低机器人的运动速度同时还会增加它的内力.如将阈值设定得太小,由于气压驱动的误差相对较大,粗略调节的过程将延长,损失了效率.在本文的样机设计中,综合考虑以上因素,将切换驱动的阈值设定为5mm.

图5 混合驱动器的控制逻辑Fig.5 Control logic of the hybrid actuator
3 驱动器长度模型
本文设计的混合驱动器中,由于弹性杆轴向刚度较高,因此认为电机驱动模式下弹性杆的轴向位移与驱动器的长度变化是一致的.但是,在气压驱动模式下,输入气压与驱动器长度的关系较为复杂.本节将建立反映输入气压与驱动器长度关系的数学模型,有助于后续控制系统的设计.
使用Fair表示气压造成的轴向伸长力,Frubber表示橡胶管的回弹力,Fmesh表示编织网套的轴向力,Fex表示驱动受到的外力.在驱动器达到静力平衡时,有以下等式成立.

使用l表示驱动器的实际长度,ˆ为原长,krubber表示橡胶管的刚度,有

使用p表示驱动器内气压值(与大气压强的差值),R表示橡胶管外半径,c表示管壁厚,有

使用ly表示组成编织网套的纤维其中一根的展开长度,n表示一根纤维绕驱动器的旋转圈数.根据文献[15-16],可知

将式(2)~(4)带入式(1),得
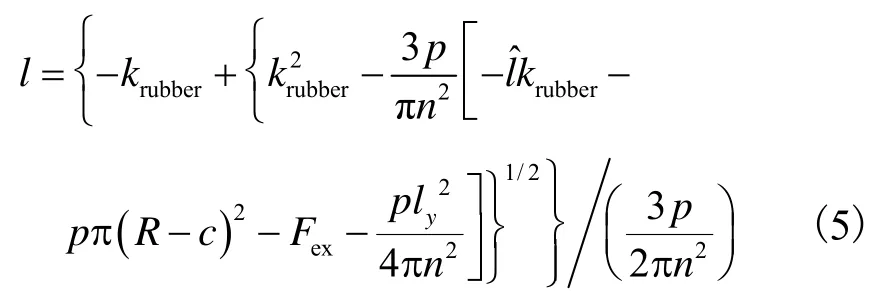
这是驱动器长度关于输入气压的显式表达.
4 实验与分析
4.1 单个驱动器测试
实验测试平台如图 6所示,将电磁位置传感器(3D Guidance tranSTAR,NDI)安装在驱动器末端来监测驱动器长度的变化.该传感器配套有电磁场发生器,而传感器本体在电磁场中的三维坐标位置可被感知.该传感器对位置的监测误差(RMSE)小于1.0mm.驱动器将在气压驱动和电机驱动模式下分别进行测试.在气压驱动模式下,以 0.025MPa的步长增加气压输入至0.250MPa,之后减小气压至0(与大气压强的差值).驱动器伸长和回复在40mm左右的一个范围内.而电机驱动模式适用于微调,该模式下驱动器的长度变化在 5mm 范围内,取步长 1mm通过直线电机来控制.实际样机中,krubber为501.4N/m,n为9圈,ly为443.3mm.

图6 驱动器测试平台Fig.6 Test platform for the actuator
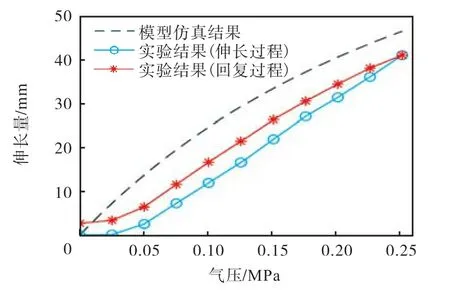
图7 气压驱动模式实验与模型仿真结果Fig.7 Experiment and model simulation results in pneumatic driving mode
气压驱动模式实验与模型仿真结果见图 7,横坐标代表气压值,纵坐标代表驱动器伸长量.实线为实验结果,虚线为本文式(5)所建立模型的仿真结果,其中假设所受的外力Fex为 0.可以看出在实验中一开始增加压力时驱动器并没有伸长,存在一段死区e,大约在 0.025~0.05MPa之间;在相同的气压输入下,回复过程中的驱动器长度总是大于伸长过程,最终当气压减至 0时,驱动器并没有恢复原长,存在明显的迟滞现象.其中气压为0.125MPa的点迟滞误差最大,为驱动器原长的 2.40%,气压为 0的点迟滞误差为1.34%;模型仿真结果显著大于实验结果,回复过程误差最大为7.94mm,在气压为0.10MPa的点.
死区存在的原因是样机中橡胶管与编织网套之间存在微小的间隙,一开始增加的气压只使驱动器发生径向膨胀,而轴向长度几乎不发生变化.提高工艺水平可以缩小死区的范围,如能将气动肌肉设计成为一体的结构有消除死区的可能,由于本文气动肌肉采用的分离设计则难以避免死区.迟滞现象则是由摩擦力产生的,包括橡胶管与编织网套之间的摩擦力、构成编织网套的每根纤维之间的摩擦力以及驱动器与外界环境之间的摩擦力.这些摩擦力总是与驱动器运动方向相反,造成了迟滞误差.而模型与仿真结果大于实验结果这个现象产生的原因是上文提到的死区,模型中微小的气压增加就能立刻引起驱动器长度的变化,因此可根据样机实验对模型做出修正.修正式(5)为

式中为死区的大小,根据实验数据取死区大小为0.035 MPa.修正后的模型仿真结果如图 8所示.将修正前后的模型仿真曲线与回复过程中死区之外的实验标记点对比,结果列在表 2中.可以看出实验与模型仿真结果的平均偏差相较于修正前从6.9mm下降到 1.1mm,这说明本文所建立的气压与驱动器长度关系修正模型是有效的.
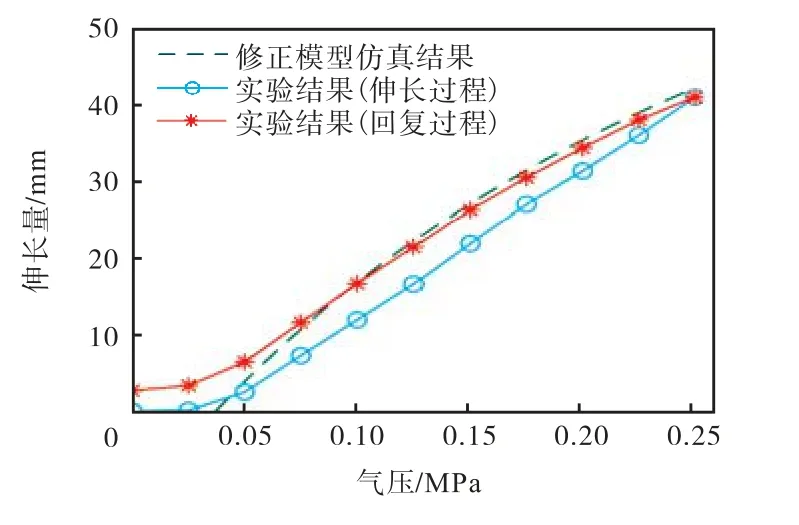
图8 气压驱动模式实验与修正后模型仿真结果Fig.8 Experiment and correction model simulation results in pneumatic driving mode

表2 模型与实验数据的比较Tab.2 Comparison between model and experiment data
电机驱动模式实验结果见图 9,横坐标为电机的位移输出量,纵坐标为驱动器伸长量.可以看出在该模式下,伸长曲线与回复曲线几乎完全重合,微小的误差可以认为是测量误差引起的,不存在迟滞现象.并且两条曲线保持 1的斜率有很好的线性度,对驱动器来说输入位移即是输出位移.这是由于弹性杆轴向刚度较大,本样机中它的弹性模量为 28GPa,近似于刚体,使得电机驱动本质上成为一种位置控制,直接控制驱动器的伸长量.而气压驱动本质上是力控制,通过控制气压达成对驱动器作用力的控制.因此,在电机驱动模式中即使同样存在摩擦力也不会产生滞环,证明了该模式适合于精确调节.

图9 电机驱动模式实验结果Fig.9 Experimental results in motor driving mode
4.2 机器人重复定位实验
为了观察机器人在两种驱动模式下的重复定位误差,采用与第4.1节实验相同的电磁位置传感器安装在机械臂的顶端连接盘上.定位实验在仅依靠气压驱动和依靠混合驱动(混合驱动模式即先进行气压粗略调节,电机再进行精确调节,如图 5所示)下分别进行10次,驱动器的长度设置为230mm、230mm和 210mm,采用闭环控制调节驱动器长度.实验结果见图 10,可以看到在两种模式下的定位点都存在散布,这是由于存在一些不确定因素,比如气体泄漏、摩擦力、迟滞和测量误差等.
从图10中能直观地看出气压驱动模式下定位点更为分散,电机驱动模式下更为集中.气压驱动模式中,定位点在x、y、z轴的坐标值标准差分别为7.05mm、2.47mm 和 9.44mm.而在混合驱动中,标准差为 2.86mm、1.14mm 和 1.63mm,平均下降了65.4%.这说明混合驱动系统有益于提高机器人的重复定位精度,原因是在切换为电机驱动模式后,机械臂的刚度提高了,抗未知因素干扰的能力得到了增强,这一点将在下一个实验中证明.

图10 重复定位实验中机器人末端点位置分布Fig.10 Distribution of the robot tip positions measuredfrom the repetitive tests
4.3 变刚度实验
本文定义机械臂的刚度为

式中:Fx为施加在机械臂顶端沿x轴方向的外力;Dx为机械臂顶端由于外力造成的在x轴上的位移量.该参数反映了机械臂抵抗外力干扰的能力.实验平台的设置如图 11所示(图中数值为驱动器长度),施加在机械臂顶端的力由力传感器读出,机械臂顶端位置的变化由电磁位置传感器监测.为了证明变刚度效果的一般性,实验选取了在 A、B、C 3种不同姿态下进行测试,如图 12所示.分别在气压驱动模式和电机驱动模式下(区别在于是否锁紧弹性杆),对机械臂顶端施加一个2N的沿x轴方向的水平力.机械臂的变形参数列在表 3中.可以看出,在气压驱动模式下,机械臂的平均刚度为 23.5N/m,本文所提混合驱动的方案依然能够保持机器人的柔顺性.在 B姿态电机驱动模式下机械臂的刚度相比于气压驱动模式变化最明显;而 A、C两种姿态下刚度较大,变化较少.这是由于B姿态下机械臂垂直,水平外力完全转化为弯矩;而 A、C这两种姿态下,水平外力的部分分力作用于机械臂的轴向.实验结果表明,3种姿态下机械臂刚度平均增加66.9%.产生变刚度的原理为在气压驱动模式下即未锁紧弹性杆时,驱动器的轴向刚度与气动肌肉无异.而在锁紧弹性杆切换为电机驱动模式之后,驱动器的轴向刚度为气动肌肉与弹性杆刚度相加,最终导致整个机械臂的刚度增加.这也证明了电机驱动模式适合于精确定位.

图11 机械臂变刚度实验平台Fig.11 Experimental platform of variable stiffness of the robot arm
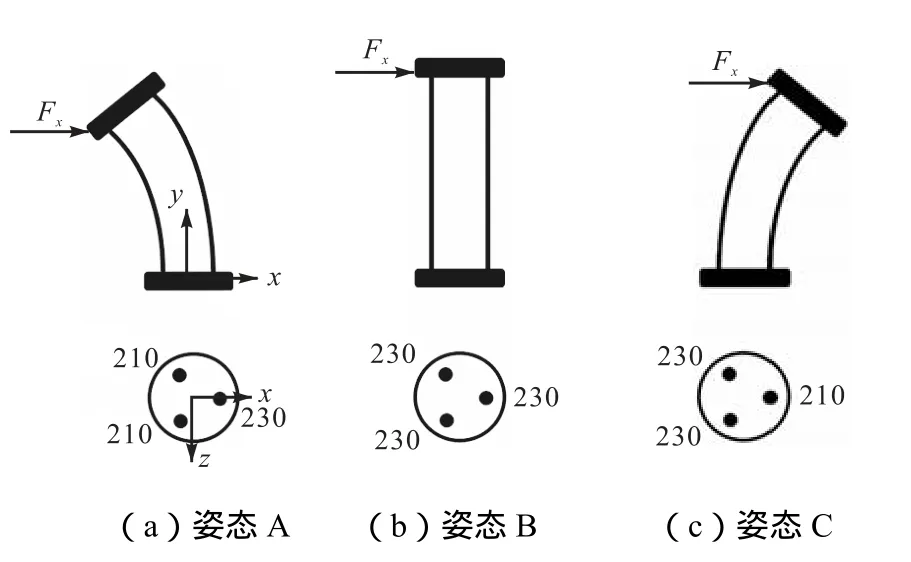
图12 机械臂刚度测试的3种姿态(单位:mm)Fig.12 Three postures of the robot arm for stiffness testing(unit:mm)

表3 机器人变形参数Tab.3 Robot deformation parameters
5 结 论
(1) 针对单一驱动方式性能不够全面的问题,提出了一种新型的混合驱动器,将弹性杆嵌入气动肌肉使它具有气压驱动和电机驱动两种驱动方式,能够通过机械的方式自由地切换.
(2) 提出混合驱动机器人,在大范围运动时采用气压驱动保持柔顺性以适应非结构化环境,在目标位置后切换为电机驱动模式,提高自身刚度并精确地调节机器人姿态.通过实验证明了混合驱动系统能够比单一气动方式降低 65.4%的重复定位误差,提高66.9%的刚度.
(3) 为提高气压驱动调节效率,建立了气压与驱动器长度的显式表达.通过实验发现了驱动器死区的存在并修正了模型.
未来的工作将基于本文提出的混合驱动机器人深入研究与之匹配的控制策略.
[1] Guglielmino E,Tsagarakis N,Caldwell D.An octopus anatomy-inspired robotic arm[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS).Taiwan,China,2010:3091-3096.
[2] Jones B A,Walker I D,Practical kinematics for realtime implementation of continuum robots[J].IEEE Transactions on Robotics,2006,22(6):1087-1099.
[3] Menciassi A,Gorini S,Pernorio G,et al.A SMA actuated artificial earthworm[C]//IEEE International Conference on Robotics and Automation(ICRA).New Orleans,USA,2004:3282-3287.
[4] Shintake J,Rosset S,Schubert B,et al.Versatile soft grippers with intrinsic electroadhesion based on multifunctional polymer actuators[J]. Advanced Materials,2016,28(2):231-238.
[5] Walker I D,Dawsona D M,Flash T,et al.Continuum robot arms inspired by cephalopods[C]// Proceedings of the 2005 SPIE Conference on Unmanned Ground Vehicle Technology Ⅶ.Bellingham,USA,2005:303-314.
[6] Kang R T,Branson D T,Zheng T J,et al.Design,modeling and control of a pneumatically actuated manipulator inspired by biological continuum structures[J].Bioinspiration & Biomimetics,2013,8(3):036008.
[7] Calisti M,Giorelli M,Levy G,et al.An octopusbioinspired solution to movement and manipulation for soft robots[J].Bioinspiration & Biomimetics,2011,6(3):036002.
[8] Xu K,Nabil S.Actuation compensation for flexible surgical snake-like robots with redundant remote actuation[C]// IEEE International Conference on Robotics and Automation(ICRA).Floarida,USA,2006:4148-4154.
[9] Kang R J,Guo Y,Chen L,et al.Design of a pneumatic muscle based continuum robot with embedded tendons[J].IEEE/ASME Transactions on Mechatronics,2017,22(2):751-761.
[10] Brown E,Rodenberg N,Amend J,et al.Universal robotic gripper based on the jamming of granular material[J].Proceedings of the National Academy of Sciences of the United States of America,2010,107(44):18809-18814.
[11] Li Yingtian,Chen Yonghua,Yang Yang,et al.Passive particle jamming and its stiffening of soft robotic grippers[J].IEEE Transactions on Robotics,2017,33(2):446-455.
[12] Shiva A,Stilli A,Noh Y,et al.Tendon-based stiffening for a pneumatically actuated soft manipulator[J].IEEE Robotics & Automation Letters,2016,1(2):632-637.
[13] Laschi C,Cianchetti M,Mazzolai B,et al.Soft robot arm inspired by the octopus[J].Advanced Robotics,2012,26(7):709-727.
[14] Pritts M,Rahn C.Design of an artificial muscle continuum robot[C]// IEEE International Conference on Robotics and Automation(ICRA).New Orleans,USA,2004:4742-4746.
[15] Leclair J,Doumit M,McAllister G.Analytical stiffness modeling and experimental validation for a pneumatic artificial muscle[C]//Proceeding of the ASME International Mechanical Engineering Congress and Exposition.Quebec,Canada,2014:V009T12A089.
[16] Doumit M,Fahim A,Munro M.Analytical modeling and experimental validation of the braided pneumatic muscle[J].IEEE Transactions on Robotics,2009,25(6):1282-1291.
