空间傅里叶分析在离心叶轮失速信号识别中的应用

刘正先，王生玲

(天津大学机械工程学院，天津 300350)

离心叶轮旋转失速和喘振造成了流场的不稳定性，限制了设备稳定工况范围，制约了设备安全高效运行．目前，主要通过观察性能曲线中峰值流量和静压脉动特征，运用时间傅里叶分析、行波能量法、相关系数法、小波分析和空间傅里叶分析对捕捉到的信号进行处理，从而判定叶轮是否进入失速状态及失速团运动规律．

Camp等[1]和 Day[2]通过观察性能曲线峰值点与失速点流量的关系，及机匣上静压是否发生突变判定失速，其准确度受经验和主观因素制约．吴艳辉等[3]通过对非定常压力频谱分析，根据失速扰动频率分析失速原因，但傅里叶变换结果是整个时间范围内的频率特性，而不能反映信号在某一时刻的本质特征．程晓斌等[4-5]、Lin 等[6]、符娆等[7]和 Zhang 等[8]等通过小波分析识别轴流叶轮内失速信号，可以在时频域内分析失速流场，但受时域和频域分辨率的制约和折中，对离心叶轮失速流场中复杂的压力信号不能得到理想的结果．

空间傅里叶分析计算简单，实时性好，不受采样频率影响，可以得到扰动信号空间不均匀程度随时间的变化规律．Garnier等[9]通过分析轴流叶轮失速实验数据的空间傅里叶结果，发现低速叶轮中振幅最大的为1阶扰动，高速叶轮中为2阶扰动，通过分析扰动相位变化，估算失速团周向运动速度．但受当时实验和计算条件限制，仅在壁面周向布置 8个静压探针，只能得到 4阶模态，无法指出阶数的物理意义.Joshua等[10]也在轴流叶轮失速实验中布置 8个周向静压探针，并通过分析1阶模态的相位变化计算失速团周向运动速度．通过实验研究虽然能够得到更真实的流场信息，但存在较大的测量局限性，使空间傅里叶结果不能细致反映流场信息．

计算流体力学的发展使叶轮全三维非定常计算开始应用于失速研究中，鞠鹏飞[11]对一轴流叶轮失速过程进行了全通道非定常计算，在周向布置与叶片数一致的 36个监视点，通过空间傅里叶分析，得出叶轮失速流场的周向不均匀度与失速团个数的关系，认为振幅最大的3阶模态对应3个失速团．

本文通过对 Eckardt[12]离心叶轮全通道非定常计算，在不同叶高、不同流向位置的周向曲线上均匀布置 1024个监视点，通过空间傅里叶结果的幅值和相位变化，研究失速流场分布和失速团运动规律，进行失速信号识别，为叶轮机械失速实时监测、主动控制、优化设计[13]和设备安全运行提供理论依据和指导．

1 数值计算

1.1 计算网格及方法

以 Eckardt离心叶轮为研究对象，选取入口段、叶轮和无叶扩压器为计算域，几何参数可参见Eckardt[12]实验测量叶轮，叶顶间隙为前缘 0.5mm、尾缘 0.7mm，设计转速为 14000r/min，设计流量5.31kg/s．通过图1所示的3种数目的网格独立性验证，考虑计算成本并尽可能显示失速涡分布，单通道网格数选择 150×104：入口段 8×104，无叶扩压器45×104，叶轮 97×104．其网格见图 2．将单通道网格绕旋转轴复制 20个形成完整叶轮网格，网格总数为3000×104，进行全通道非定常计算．

采用有限体积法数值求解三维 RANS方程并采用标准k-e湍流模型[14]．边界条件设置如下：入口轴向进气，总温 288K，总压 101325Pa，定常计算时动静交界面采用冻结转子法，以大流量工况为起始点，通过减小出口流量不断逼近失速工况．以定常计算结果作为初始条件，动静交界面选择瞬态转静子模型，给定流量出口，对设计工况点(D)、从实验失速点开始计算的两个失速工况点(S1、S2)进行全通道非定常计算，计算总时间为叶轮旋转 5圈经历时间21.427ms，时间步长为叶片通过周期的 1/20，叶片通过周期(blade pass time，BPT)定义为

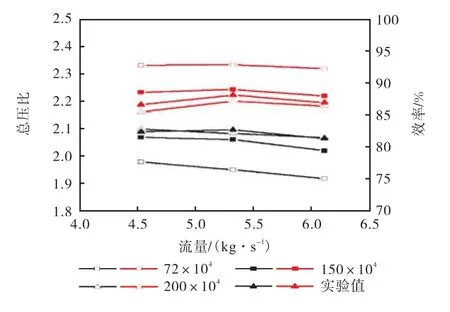
图1 网格独立性验证Fig.1 Grid independence test

式中：n为叶轮转速；Z为叶片数，对于设计转速下Eckardt叶轮，1BPT＝0.21427ms．

1.2 气动性能验证

为了验证数值计算结果的可靠性，下面进行气动性能的验证．表1给出了设计转速下离心叶轮3个工况的气动性能，与实验数据相比符合较好，最大误差仅2.21%．

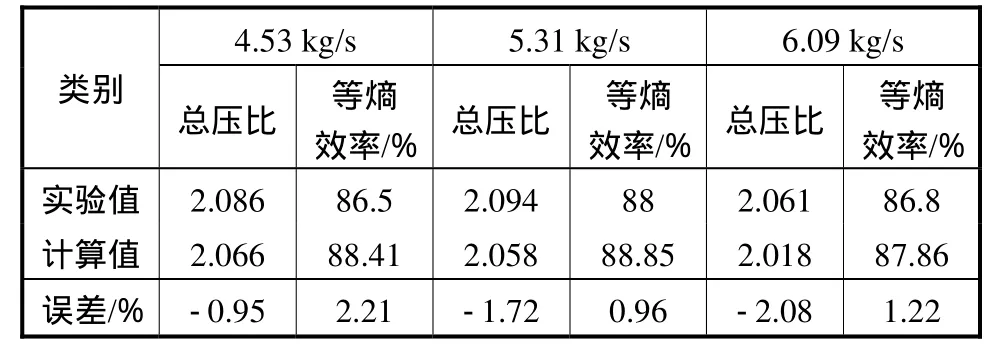
表1 CFX和实验性能对比Tab.1 Difference of performance between CFX and experiment

图 3为定常计算和全通道非定常计算总压特性曲线，计算结果与实验值[15]整体趋势符合很好，且非定常计算时均结果更接近实验值，说明本文的数值计算方法可以准确反映叶轮流场的总体特征．

图3 总压特性曲线Fig.3 Characteristics of total pressure rise

2 流场特征

为了分析叶轮不同工况下非定常流场特征，沿流向等距离做10个截面，在流向截面上给出Q准则的涡系强度，其定义为

式中Ω和S分别为速度梯度 2阶张量的对称张量(应变率张量)和反对称张量(涡张量)，其为正值时代表该区域旋转部分起主导作用．

图4为设计工况下流动涡空间分布，每个流道流动一致，在叶轮流向 70%下游开始出现由离心叶轮几何折转产生的二次涡(secondary vortex，SV)，且沿流向二次涡逐渐增大，从图 4(b)的放大图可以看出，在设计工况下叶轮下游吸力面侧(SV1、SV2)和压力面侧(SV3)存在二次涡，且沿流向到叶轮出口流动涡范围逐渐增大．

图4 设计工况流动涡分布Fig.4 Flow vortex distribution under the design condition

图 5表明在失速工况下，叶轮入口近叶顶区域80%叶高以上存在 4个周期分布的失速团(stall cells，SC)SC1～SC4，每个失速团影响范围为 5个流道，因此将叶轮每 5个通道作为一个研究对象，用黄色叶片隔开，并依次沿叶轮旋转方向(即θ正方向)编号为流道 1～5．从图 5(c)的放大图可以看出，受上游失速团的影响，叶轮流向 50%下游就开始出现二次涡，且每个流道二次涡强度不均匀，与设计工况(图 4(b))相比，失速流道 3和流道 4流动涡影响范围减小，主要在叶顶间隙区域，而上游没有失速团的流道 1和流道 2，流动涡范围与设计工况差别不大，仅位置发生改变．

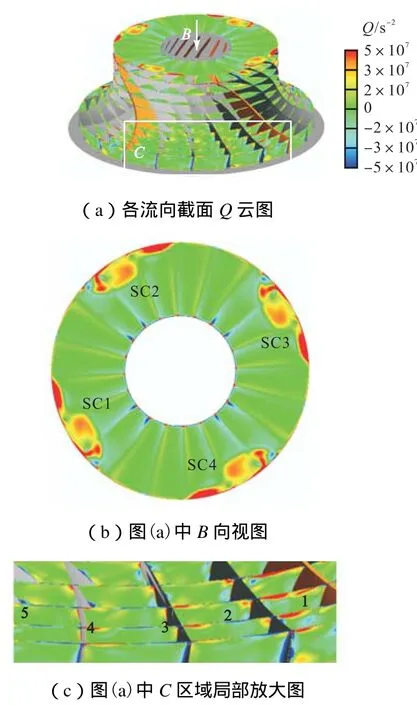
图5 失速工况流动涡分布Fig.5 Flow vortex distribution under the stall condition

3 空间傅里叶分析

3.1 流场数据监视点布置

为了较系统全面地分析失速团在径向、流向和周向的运动规律，以叶轮入口为基准，在流向(streamwise，st)定义叶轮入口为 0，出口为 100%，在径向(span，sp)定义轮毂侧为 0，轮盖侧为 100%．在90%叶高的 2%、40%和 80% 流向位置的 3条周向曲线，2%流向的 20%、40%、60%、80%、90%、95%和 98%叶高位置的 7条周向曲线上分别均匀布置1024个监视点，提取流场数据进行空间傅里叶分析；在相对坐标系中的3个流向位置某一通道内布置7个不同叶高的监视点，如图 6所示．其命名规则为流向位置用st表示，叶高位置用sp表示，即st80sp90表示80%流向90%叶高位置，以此类推．

图6 数据监视点布置Fig.6 Arrangement of the monitor points

3.2 空间傅里叶分析方法

空间快速傅里叶变换(spatial fast Frourier transform，SFFT)分析可以将周向分布的信号分解为空间坐标的简谐运动，得出各阶模态的幅值和相位．在叶轮周向曲线上布置N个监视点，其观测数据为，傅里叶级数的展开式表示为

其中各项傅里叶系数分别为

根据方程组唯一解条件可知经傅里叶变换可以得到m≤N/2阶模态．经快速傅里叶变换将N个信号分解为N/2+1个空间模态对应的复数形式的傅里叶系数，即

其幅值为

每个幅值的带宽为2/N，该信号的实际振幅

相位为

通过分析不同时刻的幅值谱，可以了解某一时刻脉动信号周向分布的不均匀度和周期性特征；通过分析幅值谱随时间的变化规律，量化失速流场随时间的变化规律；通过对主要模态的相位研究，计算得到非定常扰动传播速度和方向．

3.3 空间傅里叶分析结果

采用式(3)～(7)计算得到空间傅里叶结果的振幅，分析设计工况和失速工况叶轮入口不同叶高静压空间分布，图 7所示为 2%流向位置空间快速傅里叶变换结果．图 7表明，设计工况下只存在 20阶及其倍数阶模态，而失速工况下 20阶模态仍然存在，但明显小于4阶振幅，这与图5中显示的4个失速团一致．可见空间傅里叶分析主要模态的阶数代表该幅值的脉动信号在周向出现的次数，且幅值越大，说明该阶模态在周向周期出现的规律越显著，以此确定叶轮流场是否存在失速扰动和失速团个数．上述分析说明在设计工况下流场只受叶片通过频率影响，而失速工况下受4个失速团扰动频率的影响更强烈，且集中在 80%叶高以上，与上文失速扰动主要在叶轮入口近叶顶区域一致，且 90%叶高振幅最大，说明该位置失速团扰动最强．

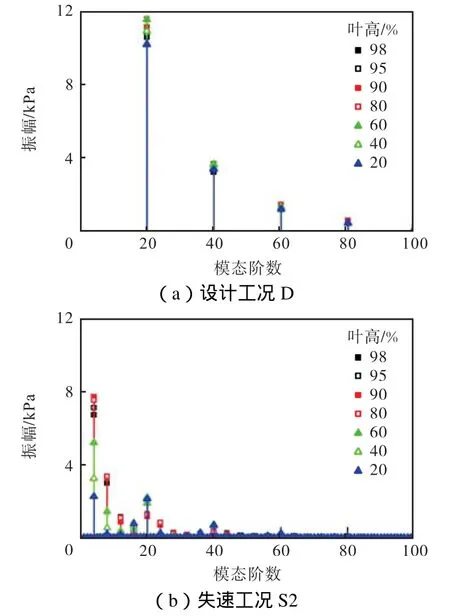
图7 2%流向位置静压空间快速傅里叶变换结果Fig.7 SFFT results of static pressure at 2% streamwise

接下来分析不同流向位置 90%叶高的空间傅里叶结果．从图 8可以看出，不同流向位置均存在振幅不同的4阶模态和振幅基本相同的20阶模态．在叶轮入口(流向 2%)，11倍叶片通过周期 BPT以前存在明显的4阶模态，即存在4个失速团，之后4阶模态振幅逐渐减小，4阶及其倍数阶模态开始在3kPa以下波动，说明此时叶轮入口出现更多(8、12或 16个)幅值更小的失速扰动；在叶片折转位置(流向 40%)，21BPT之前 4阶模态出现 4个局部峰值，说明此时失速团扰动已经影响到流向 40%位置，之后 4阶扰动开始逐渐增强，在 73BPT时达到最大值，并开始小幅波动，说明此时在该位置存在 4个明显的失速团；在叶轮下游区域(流向 80%)，17BPT之前，受上游失速团影响，4阶扰动出现了3个局部峰值之后振幅逐渐增大，在 79BPT时达到最大峰值后开始小幅波动，且该位置受叶片通过影响的20阶扰动更明显.

图8 90%叶高空间快速傅里叶变换振幅分析Fig.8 Amplitudes of the SFFT results at 90% span

综上所述，可确定叶轮中主要存在 4个失速团，且失速首先发生在叶轮入口近叶顶区域，并随着失速团的脱落、破碎逐渐向下游移动，在 14BPT之后失速团移动到叶轮流向 40%位置，在 17BPT之后失速团影响到叶轮流向 80%位置，60BPT之后叶轮流道内4阶模态振幅在6kPa以上小幅波动，此时叶轮进入深度失速工况．

为了进一步分析失速团周向传播速度，通过失速团扰动相位变化计算其角速度．

叶轮旋转的角速度计算式为

可计算出叶轮旋转角速度为1465.33rad/s．

失速团运动角速度为

可得失速团相对叶轮旋转速度的比值为

图 9给出了空间傅里叶结果 4阶扰动的相位变化，图中圆点大小代表振幅．

图9 4阶扰动相位Fig.9 Phases of the 4th mode

通过式(8)～(11)可得失速团周向运动速度，在叶轮入口时斜率更大，即运动速度更大，为0.73倍叶轮转速；30BPT时40%流向位置出现速度为0.62倍叶轮转速的失速团；40BPT时失速团到达流向 80%位置，60BPT之后，叶轮进入深度失速工况，流道内不同流向位置失速团运动速度基本一致，约 0.62～0.64倍叶轮转速．

3.4 时间傅里叶分析验证

图10 静压FFT结果Fig.10 FFT results for static pressure

为验证第 3.3节空间傅里叶方法分析失速团运动规律的可行性，对3个流向位置不同叶高监视点的静压时间信号进行 FFT分析，并用其振幅最大值归一化，最终结果见图 10．从图中可以得出，不同流向位置叶轮失速扰动信号主要集中在80%叶高以上，并且由于监视点位于相对坐标系中，没有出现振幅较大的叶轮旋转频率 233.33Hz和叶片通过频率4666.66Hz．在叶轮入口，主要存在频率为 1980Hz和2333Hz的非定常扰动，且存在振幅为0.5左右的频率分别为175Hz、757～1160Hz的扰动，说明入口失速扰动在整个数值计算时间范围内周期性不明显，存在速度大小不等的失速扰动．在叶轮折转位置和叶轮尾缘区域的失速扰动频率一致，最大振幅频率均为784Hz，且存在一个频率175Hz的扰动．

综上所述，整个叶轮中均存在175Hz的频率，应为叶轮旋转1周后失速团再次经过该监视点引起，可估算出该失速团速度约为 0.75倍叶轮转速；叶轮入口振幅最大的频率应为失速团移动一个通道引起，可估算出该失速团速度约为0.7倍叶轮转速，且存在很多其他频率的扰动，笔者推测是由于叶轮入口仅在11BPT之前存在强度较大的 4个失速团，而之后失速团脱落破碎为更多强度较小失速团，使各失速团运动速度不相等．在叶轮流道内，失速团扰动频率大约为 0.66倍叶轮转速，与空间傅里叶相位分析结果基本一致，说明空间傅里叶分析不仅可以识别失速团个数，还可以给出失速团运动规律．

4 结 论

通过对 Eckardt离心叶轮全通道非定常不同叶高、不同流向位置周向静压数据的空间傅里叶分析，以及与失速涡分布及时间傅里叶结果的对比，得出以下结论．

(1) Eckardt离心叶轮在失速工况下，周向存在4个失速团，主要集中在 80%叶高以上．叶轮失速首先发生在叶轮入口近叶顶区域，并逐渐向通道下游移动，当下游存在 4个强度稳定的失速团时，表明此时叶轮进入深度失速工况．

(2) 通过对不同流向位置周向空间傅里叶相位分析，得到失速团在周向的运动规律，失速团首先在叶轮入口以 0.73倍叶轮转速周向运动，随着失速团向下游移动，速度逐渐减小为0.63倍叶轮转速．

(3) 在离心叶轮失速流场中，失速团运动规律复杂，存在周向、流向和径向的三维运动．

综上所述，空间傅里叶分析能准确识别叶轮失速流场中的不均匀性及失速信号周向运动规律随时间的变化，可用于实时监测和失速预警，对防止失速故障、进行失速主动控制和确保设备安全运行具有重要工程指导价值．

[1] Camp T R，Day I J.A study of spike and modal stall phenomena in a low-speed axial compressor[J].Journal of Turbomachinery，1998，120(3)：393-401.

[2] Day I J.Stall inception in axial flow compressors[J].Journal of Turbomachinery，1993，115：1-9.

[3] 吴艳辉，安光耀，陈智洋，等.跨声速压气机转子近失速工况非定常流动及相关机理研究[J].推进技术，2016，37(10)：1847-1854.

Wu Yanhui，An Guangyao，Chen Zhiyang，et al.Numerical investigation into unsteady flow and its associated flow mechanism in a transonic compressor rotor at near stall conditions[J].Journal of Propulsion Technology，2016，37(10)：1847-1854(in Chinese).

[4] 程晓斌，聂超群，陈静宜.轴流压气机旋转失速先兆过程中的频率阶跃现象[J].工程热物理学报，2000，21(1)：29-33.

Cheng Xiaobin，Nie Chaoqun，Chen Jingyi.The frequency step-up of rotating stall precursors in two axial compressor[J].Journal of Engineering Thermophysics，2000，21(1)：29-33(in Chinese).

[5] 程晓斌，陈静宜.基于小波变换的离心压气机旋转失速先兆时频分析[J].工程热物理学报，2000，21(3)：289-293.

Cheng Xiaobin，Chen Jingyi.The time-frequency analysis of rotating stall inception in the centrifugal compressor based on wavelet[J].Journal of Engineering Thermophysics，2000，21(3)：289-293(in Chinese).

[6] Lin F，Chen J，Li M.Wavelet analysis of rotor-tip disturbances in an axial-flow compressor[J].Journal of Propulsion and Power，2004，20(2)：319-334.

[7] 符 娆，雷 勇.基于小波分析的压气机失速初始扰动信号处理[J].西北工业大学学报，2010，28(3)：421-424.

Fu Rao，Lei Yong.Applying wavelet analysis to processing precursor signals in compressor to obtain early warning of stall[J].Journal of Northwestern Polytechnical University，2010，28(3)：421-424(in Chinese).

[8] Zhang H D，Yu X J，Liu B J，et al.Using wavelets to study spike-type compressor rotating stall inception[J].Aerospace Science and Technology，2016，58：467-479.

[9] Garnier V H，Epstein A H，Greitzer E M.Rotating waves as a stall inception indication in axial compres-sors[J].Journal of Turbomachinery，1991，113(2)：290-301.

[10] Joshua D C，Scott C M.Analysis of axial compressor stall inception using unsteady casing pressure measurements[J].Journal of Turbomachinery，2013，135(2)：21036-1-21036-12..

[11] 鞠鹏飞.压气机旋转失速数值模拟研究[D].北京：北京航空航天大学，2001.

Ju Pengfei.Numerical Investigation of the Compressor Rotating Stall[D].Beijing：Beihang University，2001(in Chinese).

[12] Eckardt D.Detailed flow investigations within a high speed centrifugal compressor impeller[J].Journal of Engineering for Gas Turbines & Power，1976，98(98)：391-402.

[13] 刘正先，韩 博，鲁业明.目标优化算法在叶片参数化设计中的应用[J].天津大学学报：自然科学与工程技术版，2017，50(1)：19-27.

Liu Zhengxian，Han Bo，Lu Yeming.Application of the objective optimization algorithm in parametric design of impeller blade[J].Journal of Tianjin University：Science and Technology，2017，50(1)：19-27(in Chinese).

[14] 刘正先，苗永淼.有曲率影响的湍流流场中几种k-z模型的数值模拟[J].天津大学学报，2000，33(1)：98-101.

Liu Zhengxian，Miao Yongmiao.Numerical simulation of the effect of streamline curvature on turbulent flow field with threek-zmodels[J].Journal of Tianjin University，2000，33(1)：98-101(in Chinese).

[15] Eckardt D.Instantaneous measurements in the jet-wake discharge flow of a centrifugal compressor impeller[J].Journal of Engineering for Gas Turbines & Power，1975，97(97)：337-345.