橡皮胶粘球拍裂缝对乒乓球反弹轨迹偏移影响研究

邓晓明

摘要：乒乓球作为我国的国球，是我国最为普及的运动之一。橡皮胶是一种高弹性聚合物材料，变形能力较强，将其运用于球拍中能让球拍有很好的弹性。乒乓球的反弹轨迹会受到球拍和乒乓球的材料、速度等物理因素的影响。文中主要运用有限元模型法，通过研究乒乓球三个不同阶段的速度，研究橡皮胶粘球拍缝隙对乒乓球的反弹轨迹影响。

关键词：乒乓球;橡皮胶;反弹;有限元模型

中图分类号：TQ339 文献标识码：A 文章编号：1001-5922（2019）12-0123-05

乒乓球球拍是复杂的分层混合材料，包括粘合在木制片上的两个聚合物片：弹性体致密泡沫和结构化橡胶（包括规则排列的小圆柱体），即所谓的紧凑型。橡皮胶是具有可逆形变的高弹性聚合物材料，在室温下富有弹性，在很小的外力作用下能产生较大形变，除去外力后能恢复原状[1]。对于球拍对乒乓球的影响研究，武秀根等人利用商用有限元软件MSC.MARC，通过对乒乓球与球拍碰撞过程的数值模拟，着重研究由传统木材和碳纤维复合材料板叠合而成的乒乓球拍的微结构对碰撞乒乓球运动规律的影响，为优化设计新型球拍提供理论依据[2]。习星等人认为乒乓球运动是一项学生习惯且熟悉的体育运动项目，其与物理学研究有着密切的联系。以该运动项目为情境，分析了乒乓球运动过租中的受力特点，并结合平抛运动和斜抛运动的规律探索它的轨迹特征和落点规律[3]。将橡皮胶用于乒乓球拍的裂缝中能起到很好的作用，当乒乓球撞击在球拍上时其反弹效果会如何呢？文中将采用有限元方法系统地研究乒乓球对橡皮胶粘裂缝的球拍的自由影响，并揭示球的详细动态特征。

1 有限元模型

图中1a和b分别为乒乓球的示意图和有限元模型，该乒乓球自由地撞击到具有初始速度VO的静止球拍上，其中R和h分别表示乒乓球的平均半径和壁厚。

在2000年悉尼奥运会举办之前，国际标准乒乓球的外径和质量分别为D=38mm和m=2.5g，然后由ITTF正式监管为D=40mm和m=2.7g，以减缓比赛期间乒乓球的速度，使游戏对观众更具吸引力。乒乓球通常由赛璐珞制成，这是一种轻质且柔韧的塑料，具有高拉伸强度。据文献报道，赛璐珞材料的密度约为p=1400～1600kg/m3，因此，38mm或40mm乒乓球的平均壁厚约为h=0.4mm，对于38mm球，平均半径约为R=18.6mm，对于40mm球，R=19.6mm[4]。

由于成分和制造工艺不一致，所出现的赛璐珞材料的机械性能因情况而异，尚未正式提供。为简单起见，在本研究中，乒乓球的赛璐珞假定为线性弹性且完全是塑性的，而材料的密度，弹性模量和屈服应力取p=1400kg/m3，E=2.2GPa和Y=50MPa。因此，材料的屈服速度为VY=28.5m/s。

ABAQUS/Explicit用于在本研究中进行模拟。对乒乓球的碰撞和回弹过程进行了模拟，并且已经证实半球模型的模拟结果与完整球的模型非常相似，只要從轴对称变形模式到非轴对称变形模式的过渡不是一个模型。因此，只有一半乒乓球在ABAQUS/CAE下建模以节省计算成本，同时施加适当的对称边界条件[5]。使用壳体元件S4R（4节点通用壳体，有限膜应变，减少积分和沙漏控制）和S3（3节点三角形通用壳体），通过墙壁有五个高斯积分点，球的壳体离散化一模拟弯曲变形的厚度。为了节省计算成本，球的表面在ABAQUS/CAE中被划分，并根据变形梯度分配不同水平的网状种子，如图中1b所示，并且指定给接触区域的最细网格尺寸是约为平均半径R的1/50。球与球拍之间的相互作用被建模为具有正常“硬”接触的表面对表面接触对，并且切向力学性质被认为是无摩擦的，而效果是系数偏离的详细研究。

在ABAQUS/Explicit中引入了两种形式的体积粘度，线性体积粘度和二次体粘度，以提高高速事件的建模精度。结果发现，当乒乓球在碰撞过程中发生屈曲时，ABAQUS中提供的线性体积粘度0.06的缺陷值是不合适的，这意味着在模拟过程中“人为”消耗了相当大量的粘性能量，导致能量不合适耗散和不准确的恢复系数（COR）。因此，当乒乓球弯曲时，线性体粘度参数调整为0.01-0.001。

COR在测量碰撞期间的全局能量损失中起着关键作用，如应力波传播，材料粘度和可能的塑性变形等结果。通常通过以下三种方式之一来定义COR：

其中e1，e2和e3分别表示牛顿（运动学）、泊松（动能）和高能COR，Vr和Vi是碰撞前后碰撞体的相对速度，IC和IR是压缩持续时间tC内的脉冲。并且恢复时间tR、Er和Ei分别是碰撞前后碰撞体的动能。在这些表达中，定义（1a）是最直接和最广泛应用的，因此在本文中使用。

ABAQUS中提出了Python脚本，一种面向对象的脚本语言，用于在仿真模型复杂或重复时提高ABAQUS/CAE的预处理和后处理效率。因此，本研究开发了基于python的代码，以有效的方式处理众多的仿真案例。

2 结果

基于对问题的尺寸分析，很明显，以下三个无量纲参数主导了球的碰撞和回弹轨迹行为：①壁厚与平均半径之比，η=h/R;②球的初速度与材料的屈服速度之比，v0=V0/VY;③材料的屈服应变，εY=Y/E;事实上，可以很容易地证明εY=VY/Ve其中Ve= 表示材料的弹性波速。

因此，在以下各节中将仅全面模拟和讨论这三个参数的影响。首先在模拟中选择前一节给出的球的几何和材料属性，然后逐渐增加球的初始速度。所产生的球的碰撞和回弹轨迹行为在很大程度上取决于初始冲击速度，而不同的特征则与以下三个冲击速度范围有关。

2.1速度范围I：弹性碰撞，无屈曲

图2示出了当球的初始速度为V0=0.5m/s时，在乒乓球的不同位置处与橡胶粘接裂缝的球拍的冲击力（F）和位移（u）。这里，相互作用力F0=Kh和碰撞特征持续时间τ将在下面给出。

根据初步模拟结果，在压缩球时可以合理地引入以下假设：①如图3示意性所示，球的帽部分ACB通过碰撞到球拍上而变平，然后搁置在其上;②球的变形局限于冲击端周围（即，在帽ACB内），这意味着如图3所示，球的剩余部分ADB保持不变形并朝向刚性移动目标与初始速度;③相互作用力与扁平化引起的位移之间的关系与静态压缩下的相同。

从图2c可以清楚地看出，在压缩阶段和恢复阶段期间F/F0几乎等于δ/h。即使初始速度非常低，冲击力也会发生冲击，压缩阶段和恢复阶段的冲击力非常大。不同的路径，导致COR在理想的彈性碰撞下远远低于1.0。

2.2速度范围II：具有可恢复屈曲的动态变形

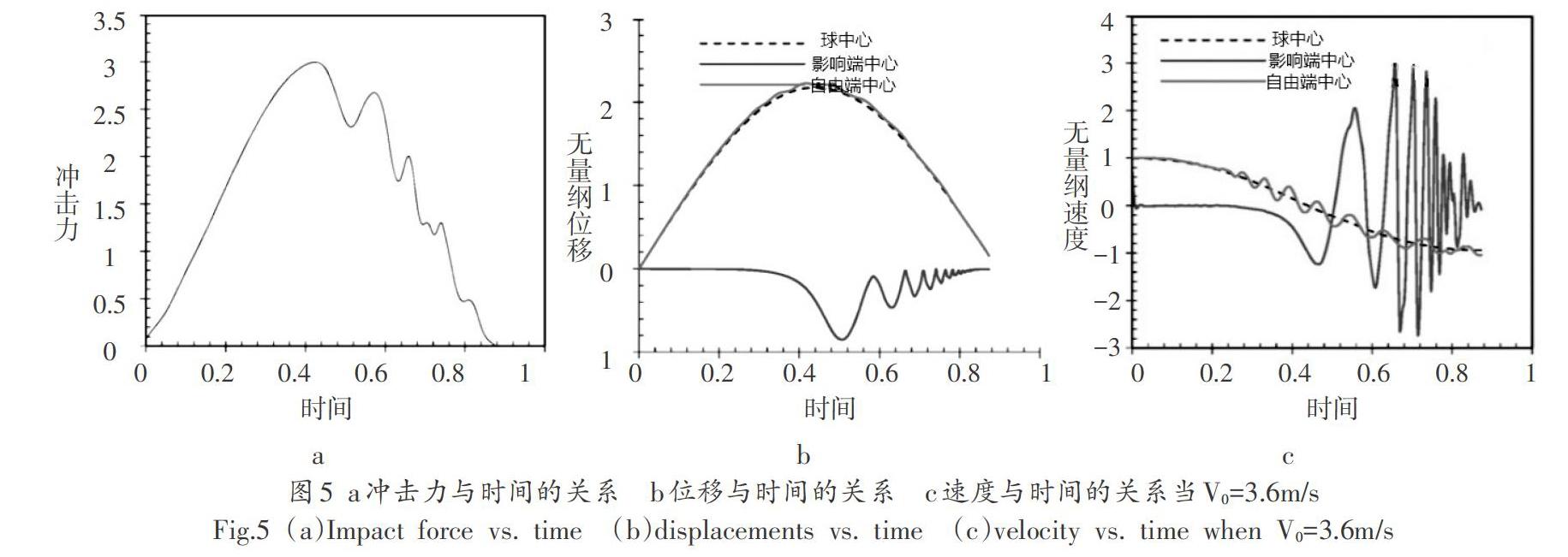
随着初始速度的增加，图4和图5分别显示了当初始速度为V0=3.4m/s和V0=3.6m/s时球的不同位置的冲击力、位移和速度。可以看出冲击端的中心在压缩阶段结束时，它开始向球的内部移动，如图4和图5所示。如图4b和5b所示，然后在恢复阶段期间振荡，图4c和5c表示帽的弯曲或向内翻转。此外，冲击端的中心的振动速度可以达到整个球的初始速度的三倍。它也可以从图中找到。在图4a和5a中，由于盖子的振荡和弯曲，当初始速度从V0=3.4m/s增加到V0=3.6m/s时，在恢复阶段期间在冲击力中出现一些突刺。因此，使空心球弯曲的最小初始速度约为V0=3.5m/s。

当球的位移到达临界值δ=ah时，球的帽开始弯曲，其中因子α在2和3之间，主要取决于球的厚度比η=h/R和材料纯弹性时的泊松比。通过球拍静态压缩球的模拟，发现具有上述给定性能的乒乓球的α接近α=2.2，而帽的屈曲几乎是弹性的，因为在移除加载板后它可以完全恢复。还应该从图1和图2中注意到，在图4b和5b中，在静态压缩下获得的屈曲条件δ=αh对于速度低时的碰撞情况仍然有效。可以推出临界速度几乎与材料的弹性波速度成比例，并且与球的厚度比h/R的3/2幂成比例。

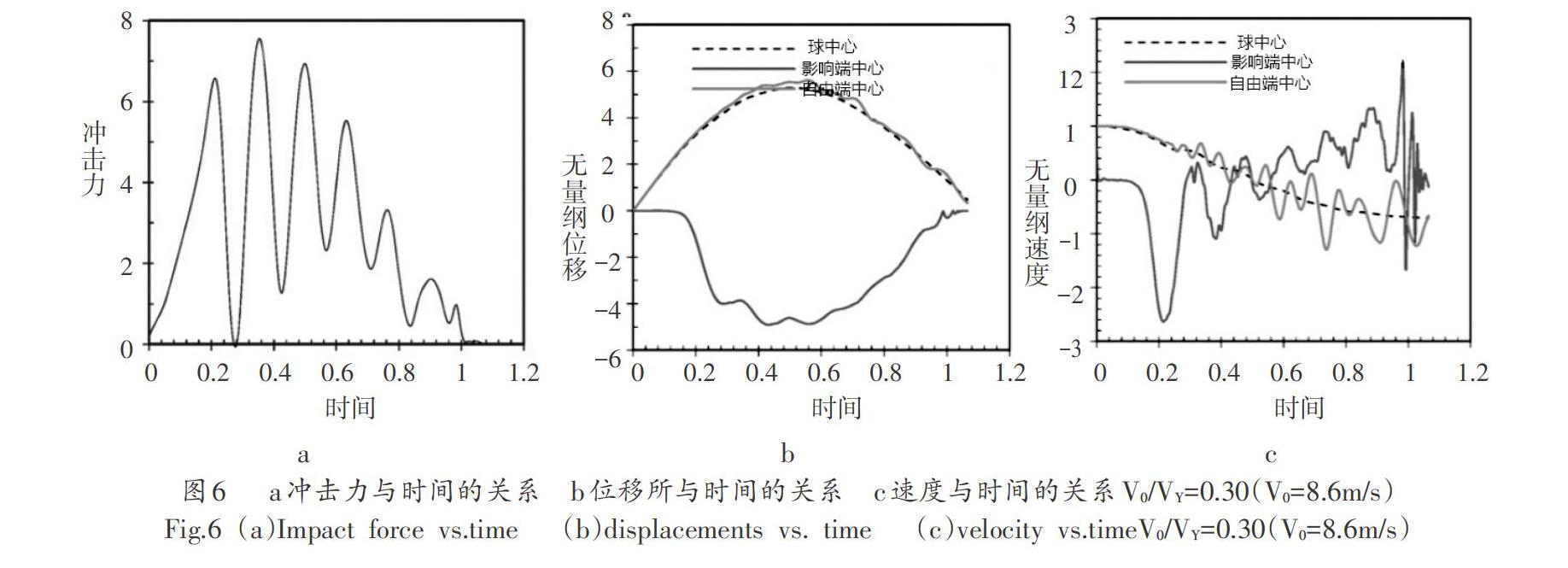
当初始速度达到V0/VY=0.30（即V0=8.6m/s）时，如图6所示，球的顶盖在压缩阶段开始非常快地弯曲并且撞击明显振荡力可以在图6a中找到。球从刚性目标完全弹回后球的变形可以恢复，但是球的回弹速度远低于初始速度，如图6c所示，这是球能量转移到弹性振动的结果（特别是盖子的那个），以及盖子向内翻转期间可能的塑性能量耗散。由于帽的振动，球和球拍在它们第一次分离后不久可能相互接触数次。这导致多次撞击的发生，因此恢复持续时间将增加。

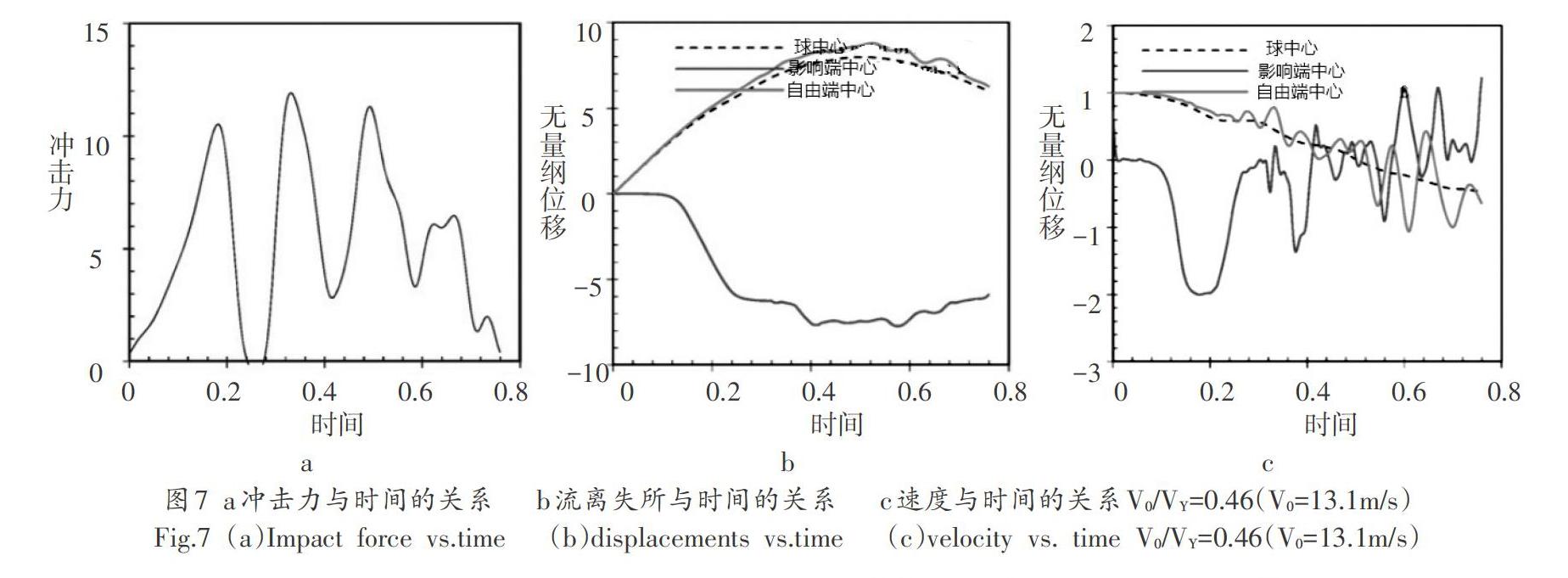
2.3速度范围III：具有永久凹痕的轴对称屈曲

当初始速度达到V0/VY=0.46（即，V0= 13.1m/s）时，如图7所示，乒乓球的屈曲将不可恢复并且由于塑性变形而将留下永久性凹痕，而恢复阶段的多重影响消失。此外，发现球完全从目标反弹后的永久性凹痕是轴对称的。由于大量的初始动能通过帽内和帽周围的塑性变形消散，因此发现球的回弹速度低于球的初始速度的1/4，导致COR小于1/4。

3 结语

综上所示，对乒乓球在橡皮胶粘裂缝的球拍上碰撞时的反弹情景进行研究，通过实验研究法和数学模型的方法，知道了乒乓球厚度与半径比、材料屈服应变和无量纲初始速度会对其与球拍碰撞的反弹轨迹产生影响，当速度越快时，由于乒乓球向内凹更多，其反弹轨迹的误差会更小。而且橡皮胶粘接的球拍缝隙能够有助于乒乓球的运行。

参考文献

[1]杨凯，沈一丁，马国艳.天然橡胶制备无毒有机乒乓球拍面粘合胶水的研究[J].高分子通报，2017（9）：40-44.

[2]武秀根，郑百林，贺鹏飞.乒乓球拍微结构对乒乓球与球拍碰撞过程的研究[J].体育科研，2006，27（2）：59-61.

[3]习星，曾澎.乒乓球的轨迹与落点研究[J].中学物理教学参考，2018（18）：78-79.

[4]唐玉生，顾军渭，李洪春，等.β-SiCw/赛璐珞纳米复合材料的制备与研究[J].塑料工业，2007，35（10）：22-25.

[5]谢聪锋，李春，任杰，等.新材料乒乓球碰撞动力学分析[J].天津体育学院学报，2017，32（1）：22-25.