基于神经网络模型的固体火箭发动机试验数据智能诊断方法
2019-02-06卫莹王凯南林
卫 莹 王 凯 南 林
中国航天科技集团第四研究院401所 陕西 西安 710025
1 引言
固体火箭发动机地面试验是一项高风险、高投入、高能耗、不可逆的试验项目。随着试验技术的发展,试验测控系统流程可靠性不断提高,能够做到主要参数获得完整无失误。但在试验过程中工况较为复杂,不可避免地受发动机工装、传感器损坏、线缆高温烧蚀、测量块掉落等因素影响,导致试验数据歧义。
对于定型阶段的发动机,性能参数稳定,试验环境、统计特征不随时间变化而变化。因此,在工程实际应用中,将固体发动机地面试验过程看作平稳随机过程,可以应用多种数据处理方法,如人工神经网络模型、时间序列等目前应用较为广泛的机器学习、人工智能方法,此类方法已经在航空领域和液体火箭发动机数据分析中有了一定的应用。但目前,尚未在我国的固体火箭发动机试验领域展开应用,基本上仍然采用传统的数据处理方法,当试验数据出现歧义时,无法判断故障原因属于测控系统故障还是发动机本身故障,需专家进行经验判读,有一定的误差。
2 歧义参数的检验方法
2.1 神经网络模型检验歧义参数的方法 固体火箭发动机试验各参数之间具体的函数关系形式较难获得,而人工神经网络模型具有非线性映射与泛化能力,一个3层BP神经网络能够实现对任意非线性函数进行逼近(根据Kolr nogor ov定理),如下图1所示。
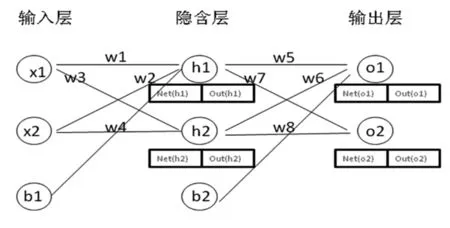
图1 三层神经网络
选择对发动机设计影响较大的推力数据作为输出神经元节点,输入层选择与输出层相关的压强、位移、应变、温度这些参数。设此系统方程具有m维输入向量和n维输出向量,xi{ }为各输入参数点值,fi{ }为输出参数点值,x=(x1,x2,…,xm)T,f=(f1,f2,…,fn)T,网络对 应m个 输 入节点、n个输出节点,zi为系统识别函数,也称为激活函数,可以选择线性函数,s形函数等。系统方程如下所示:

设神经网络有M层,第i层的节点数为ni,为第l层节点i的输出,则

此时,根据现有的人工神经网络BP算法,系统方程中的权重系数,使用有导师学习方法,给定目标函数为g w()min:
即在给定输入参数{X,F}后,使得目标函数最小
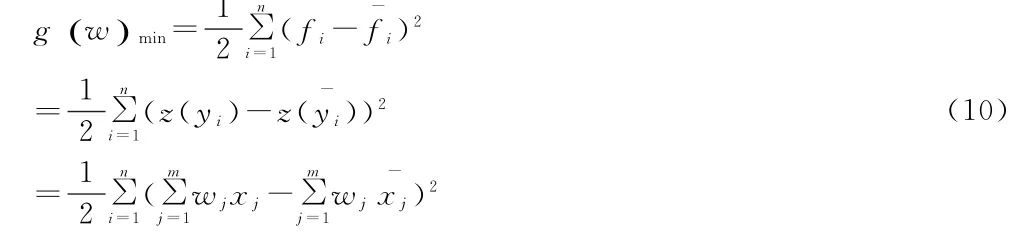
本文改进人工神经网络BP算法,将权向量的估计方法改为最大似然估计,新算法命名为BP-ML算法,
因为各参数值xi{ }均是随时间变化而变化的过程量,假定xi{ }是一个Gaussian过程,满足AR(P)模型,即用此时的公式(11)代替BP算法中的公式(9),

其中假设白噪声εm~i.i.d.N(0,σ2),(X1,X2,…,XM)满足均值为μ,协方差为Σ的正态分布。设(xp+1,xp+2,…xp+m)T为AR(P)序列的一个输入样本。则:

其中Σ为协方差矩阵:
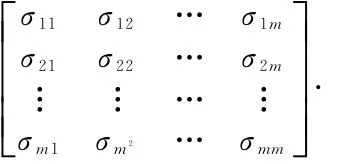
我们的目标为基于观测值xp+1,xp+2,…xp+m,估计未知参数σ2,a1,a2,…,ap的值,记θ=(σ2,a1,a2,…,ap),令x1,x2,…,xp为未知参数。公式(11)可变为:

所以基于观测值xp+1,xp+2,…xp+m,我们可得
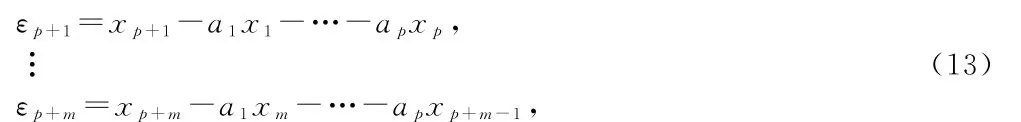
则(εp+1,εp+2,…,εp+m)的联合概率密度为

则似然函数为
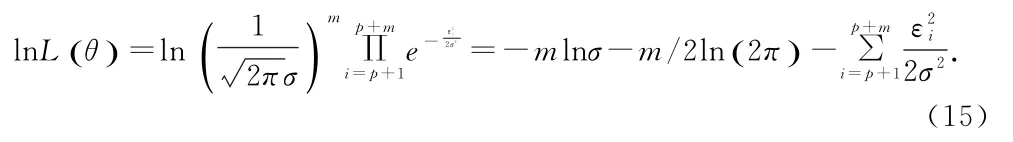
进而似然方程为

其 中1≤i≤p,1≤l≤p。
首先由于我们假定模型为p阶自回归模型,所以a1,a2,…,ap≠0,根据=0,1≤i≤p可得εp+1=εp+2=ε2p=0。进而能够解得σ2的极大似然估计为:

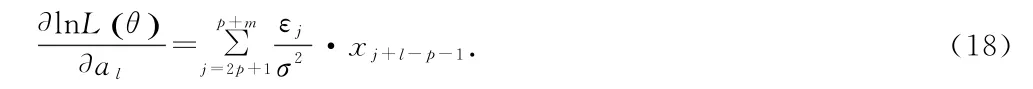
当l=1,2,…,p时

其中εj=xj-a1xj-p-a2xj-p+1-…-apxj-1,将此式代入(19)得

由(20)可解出参数a1,a2,…,ap的值,进而可以得到参数μ,Σ的值。
即目标函数g w()min中,公式(9)的方程已通过建立AR(P)模型,并通过极大似然估计方法求解出未知参数,此时ai值即为wi值,代入方程(10)中,即可求出g( w)min最小时,输出样本值,达到信号重构目的。
BP-ML算法步骤:
1.给定系统一个样本输入值{Xi,Fi};其中xi{ }为输入层,对应发动机试验中的压强、位移、应变、温度这些参数,为已知,fi{ }为输出参数值,为未知,为期望输出参数值,对应为发动机试验中采集到的推力数据。
2.计算xi{}各输入参数点值的AR模型系数,此系数即为wi;
3.选择激活函数Zi,构造系统方程Fi=Zi(Xi),计算网络输出Fi;
5.对每个样本值重复步骤1-4,直到对整个样本集,误差不超过规定范围。
在具体应用中,因为上文的BP-ML算法估计权值过程较为复杂,在精度要求较高的情况下适用,因此,下文实例中还是应用BP方法实现。
3 实证分析
判定标准
恢复值的误差判断由信号均方根作为评判标准,
信号均方根(SMSE)公式如下:

根据神经网络得到恢复值的效果采用不同时延的相关系数(DDCC)来评定,可以判断恢复值和目标值的相关程度,DDCC值越接近于1,表明相关程度越高,恢复值得到的精度越高,建立的神经网络越准确。给定相关系数阈值为5%,即≤0.05,则认为相关性高。
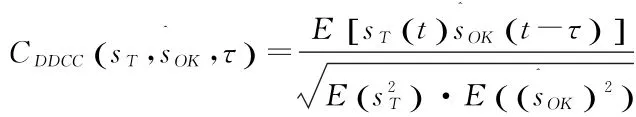
其中:sT为目标输出,为恢复值,τ为时延值。
下面通过具体的实施例子并结合附图对本文作进一步详细的描述:
步骤一:建立神经网络,训练得出网络权重值;应用三层BP人工神经网络,选取十二发某批抽型号试验数据的主要参数推力F与压强P作为研究对象,分别选择8发数据的推力F值与压强P值,输出层选择反映发动机工作状况的关键参数压强值P1作为目标输出,隐层神经元节点数选择需综合考虑训练效率与训练效果,节点数选择为50,训练效果最理想;激活函数选择双极s形函数,因为其值域在[-1,1]之间,而最大压强值达到105k Pa,因此将所有输入值与目标值均缩小10-5即可。
初始权值矩阵赋随机数,开始训练网络,当误差达到预定要求后,将此时的权值保存,即可输入发动机试验数据作为测试样本,代入权值计算,进行参数检测。
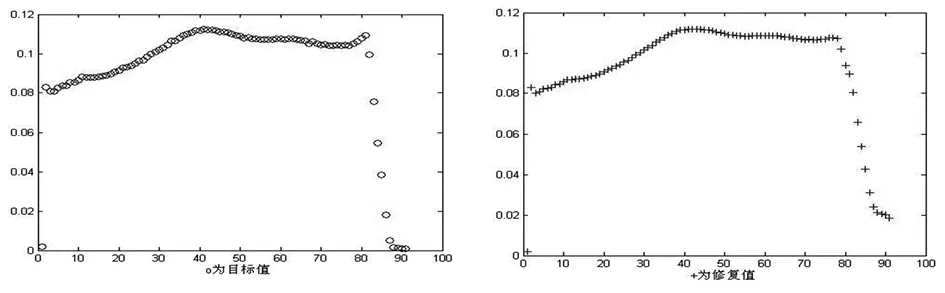
图2 目标值与修复值
图3 表示了目标值与修复值相关性,可以看出源信号与分离后信号相关程度较高,;并且在不同的时延下,相关系数有不同程度的提高,在τ取7时,CCDD的值最大,表明相关程度最高。SMSE=2.8687。C=1.0008,即目标值与修复制的误差精度在0.08%。
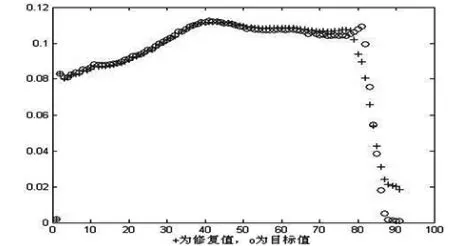
图3 目标值与修复值相关性

图4 CCDD相关系数
步骤二:歧义参数判别;为避免将正常数据误判为歧义,检测时误差阈值应大于训练误差阈值。将此时的权值保存,我们将P9中的40个点值人为扩大十倍,构造歧义的参数wP9,输出目标值为P1,得到修复后的P1见下图所示,无论时延值τ取任意值时,≥0.05,即修复后的P 1与目标值P 1相关性较差,由此可反推出输入值中有歧义参数。同理,在我们构建的神经网络模型的前提下,想判定某一发的F、P是否有歧义,则将输入值中的F、P值替换为需要判定的参数,输出目标值不变,得到修复后的值进行比较,观察相关系数是否在规定的阈值内,即≤0.05,若满足,则无歧义参数,若不满足,则有歧义参数,进一步替换检测值,判定具体的歧义参数。

图5 目标值与修复值相关性
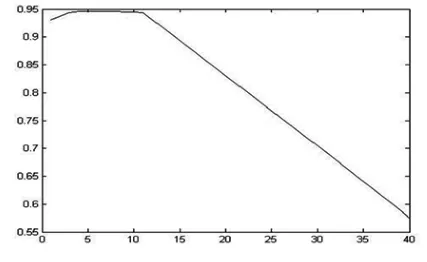
图6 CCDD相关系数
步骤三:歧义参数修复;根据我们训练的神经网络模型,判定出w P9为歧义参数后,
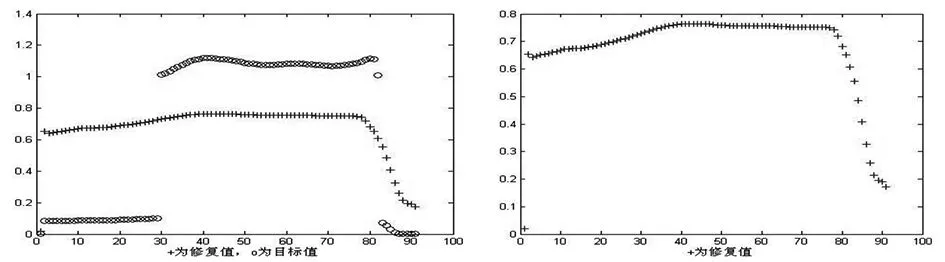
图7 歧义参数w P 9修复后的值与目标值对比图
需要进行歧义数据修复,则将图1中的输出层神经元节点设为要恢复的目标参数wP9,输入层神经元节点中去掉目标参数,分别建立各关键参数的数据,重构神经网络,训练方式同前。
4 结束语
本文研究了一种可以对固体火箭发动机试验中歧义数据的智能自动化诊断系统,第一步应用t检验检查出歧义点值,第二步设计BP-ML算法,根据三层神经网络检验出歧义参数,并进行参数值重构,减少人为经验判断的误差,建立歧义数据故障诊断系统。并改进了传统人工神经网络中权重的获得方法,改为将输入发动机各参数值xi{}假定是一个Gaussian过程,满足AR(P)模型,通过极大似然估计法求得权重值。与现有技术相比本文具有的特点是符合固体发动机试验数据特性;应用广泛;构造完整的歧义数据检验系统;完成歧义数据重构过程。
