基于改进模糊聚类分析的电力系统不良数据辨识

高金兰， 康迪， 雷星宇， 朱佳丽

(东北石油大学 电气工程学院，黑龙江 大庆 163318)

0 引 言

电力系统不良数据的检测与辨识是电力系统状态估计的重要功能之一，它能够排除量测采样数据中偶然出现的少量不良数据，提高状态估计的可靠性，确保电力系统正常稳定的运行。目前，不良数据检测与辨识的方法主要是基于状态估计的方法，包括目标函数极值检测法、加权或标准化残差检测法和量测量突变检测法等方法[1]。这些方法的缺点是很可能出现残差污染和残差淹没现象，从而引起不良数据的误检和漏检。

近年来，越来越多的新理论、新方法被应用到了电力系统不良数据检测辨识当中。文献[2]提出了利用模糊数学中的ISODATA方法和隶属度概念来判定不良数据，一定程度上克服了残差污染和残差淹没现象。文献[3]引入基于贝叶斯数据处理策略的扩展卡尔曼滤波算法及局部加权投影回归策略对电网参数进行在线检测辨识，该方法具有较高的精度。文献[4]将图论和蚁群优化算法结合起来，依据灵敏度分析法进行不良数据检测辨识，具有较快的计算速度。

模糊C-均值算法(Fuzzy C-means Algorithm, FCM)[5-6]是解决模糊聚类问题的经典算法，该方法是将聚类分析归结为一个带约束条件的非线性优化问题，相对于其他的聚类算法，FCM算法有着设计简单、应用范围广泛等优点。但模糊C-均值算法也存在对算法初始值敏感，易陷入局部最优的缺点。万有引力算法(Gravitational Search Algorithm, GSA)作为一种智能寻优的新算法，具有较强的全局搜索能力。本文在传统万有引力搜索算法的基础上提出增强型万有引力搜索算法(Enhanced Gravitational Search Algorithm, EGSA)，以标准残差和两相邻采样时刻的量测数据差值作为特征值进行聚类，以EGSA算法获得的较好的初始划分为基础，运用FCM算法进行模糊聚类，获得良性数据和不良数据的分类，最后通过COS聚类有效性判定指标判断最优聚类数目，得到最佳聚类结果，辨识出量测数据中的不良数据，将该方法应用于IEEE14节点电力系统和大庆某区域电网中，结果表明本文所方法能够有效避免误检和漏检的发生，检测结果更加准确。

1 万有引力搜索算法

1.1 传统GSA算法

万有引力搜索算法(GSA)[7-8]是通过模拟个体间的万有引力作用引导搜索。在该算法中个体j在第t次迭代中作用于个体i的力定义为：

(1)

个体i在第d维空间上受到其他个体的合力及其加速度：

(2)

(3)

式中：randj取[0,1]区间内的一个随机数，以增加算法的随机性;Mii(t)表示个体i的惯性质量。

(4)

(5)

G是关于t的一个函数：

(6)

式中:G0是万有引力常量G的初始值;α为衰减系数，通常取20;T为最大迭代次数。

引力质量和惯性质量通过下式更新：

Mai=Mpi=Mii=Mi,i=1,2,…,N

(7)

(8)

(9)

式中:fiti(t)表示个体i在时间t的适应度值。best(t)和worst(t)定义如下：

(10)

(11)

1.2 增强型万有引力搜索算法(EGSA)

在传统GSA算法中，搜索算子位置的更新是由其受到的引力作用决定的，表现形式则为加速度a的值直接影响算子的搜索步长，决定算法的全局搜索和收敛性能，并且GSA算法中α取值一般根据经验为一个定值，这导致算法在处理某些多峰目标函数时收敛过快而陷入局部解。为此改进α的取值方式，在算法前期使其取较小值，即增大了每次迭代的搜索步长，使得搜索域变大，增强全局搜索性能。在算法后期取较大值，减小搜索步长，使得精细搜索得到最优解。

同时，引入种群多样性指标ED[9]，该指标能有效反应个体在种群搜索空间内的分布情况，通过其分布情况体现算法的成熟度。其表达式如下：

(12)

多样性指标ED的取值范围是(0,1)，ED值越小，则种群多样性较低，反之则种群多样性较高。同时引入进化程度指标参数CM，其表达式如下：

(13)

式中:fitave(t)为t时刻粒子适应度之和的平均值。

进化程度指标的取值范围是(0,1)，其值越高则种群进化成熟度越高，反之则越低。

基于以上，改进的EGSA算法中衰减系数α的取值如下：

α(t)=α(t-1)+C2×(ED-CA)+C3×(CB-CM)

(14)

式中:α(t)为第t次迭代的衰减系数;α(t-1)则为t的上一次迭代的衰减系数;C2和C3分别为多样性和成熟度的修正系数;CA和CB为多样性和成熟度的对比系数;CA和CB一般取值为(0.3,0.7)。

通过式(14)获得每次迭代衰减系数的修正值，进而得到万有引力常量的修正值。同时本文提出一种新的个体的速度更新方式，计算公式如下：

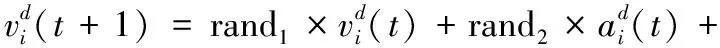
(15)

式中:随机数randi∈[-1,1];i=1,2,3;pbi表示个体i搜索到的个体最优位置;c为学习因子，控制c的大小可以调节个体向着个体历史最优位置移动的速度。

2 增强型万有引力搜索-模糊c均值算法(EGSA-FCM)

在EGSA-FCM算法中，为将个体的搜索位置与样本的隶属度建立起对应关系，将个体的位置矩阵表示样本与各个聚类簇的隶属程度，用一个n行c列的矩阵代表每一个搜索个体的位置：

(16)

其中由EGSA个体的速度更新公式得到个体新的位置,更新式(4)为矩阵计算。其中，需要确保矩阵中的元素满足如下约束条件:

μij∈[0,1],i=1,2,…,n,j=1,2,…,k

(17)

(18)

(19)

当位置矩阵中的元素违背以上约束条件时，采用以下方法修改矩阵中的元素：

(1)修改矩阵中的负值元素，将其赋值为零。

(2)当矩阵中某一行元素全为零时，则随机生成一组[0,1]的数，且使该组数的和为1。

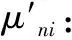
(20)

EGSA-FCM算法计算流程如下：

(1)输入聚类数目c、模糊指数m、群体规模M、最大迭代次数等参数。

(2)初始化种群以及种群中每个个体的位置和速度。

(3)计算个体的适应度值，并记录适应度值和个体历史最优位置。

(4)更新万有引力常量和惯性质量，并计算个体受到的F和a。

(5)更新个体的位置，满足迭代终止迭代次数时转步骤6，不满足时回到步骤3。

(6)更新隶属度矩阵U和聚类中心V。

(7)满足迭代终止条件时输出聚类结果，不满足时回到步骤6。

3 基于EGSA-FCM算法的电力系统不良数据辨识流程

在不良数据的辨识中，以标准残差RN和两相邻采样时刻的量测数据差值ΔZ作为特征值，得到原始样本数据集。对包含标准残差RN和相邻采样时刻量测数据差值ΔZ的特征指标矩阵实施离差标准化处理，变换公式如下：

(21)

采用EGSA-FCM算法对经过规格化处理的数据进行聚类，得到样本集不同聚类数目下的聚类划分，本文采用COS聚类有效性指标判定最佳聚类数目，最终获得最佳聚类结果，其中COS聚类有效性指标定义如下：

(22)

COS聚类有效性指标包含了C,O,S三个聚类度量因子[10]。当该指标函数值越大时，得到的模糊聚类划分结果越好，同时该极大值指标对应下的聚类数目即为最佳模糊聚类数。

基于EGSA-FCM算法的不良数据辨识流程如下：

(1)初始化特征矩阵U0。

(2)初始化最大迭代次数Nmax及其他参数，初始化种群，初始化个体的速度和位置。

(3)通过EGSA算法更新个体的位置直到满足最大迭代次数。

(4)初始化COS聚类有效检验指标中的参数。包括类内紧致阀值、类间重叠阀值等，获取COS指标值。在一次FCM算法得到聚类划分后，计算COS有效性指标值，记录不同聚类数目下的指标值。

(5)对比所有COS指标值，取最优COS值对应的聚类数目，即为最佳聚类数。

(6)输出最优聚类数目下的聚类结果，得到不良数据分类。

基于EGSA-FCM算法的电力系统不良数据辨识的简要流程如图1所示。

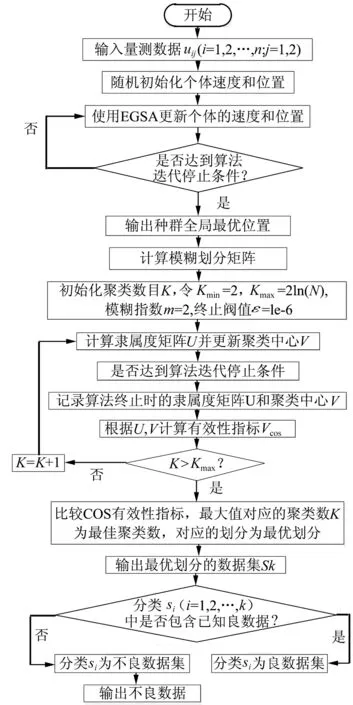
图1 基于EGSA-FCM算法电力系统不良数据辨识流程图

4 算例仿真

4.1 IEEE14节点电力系统

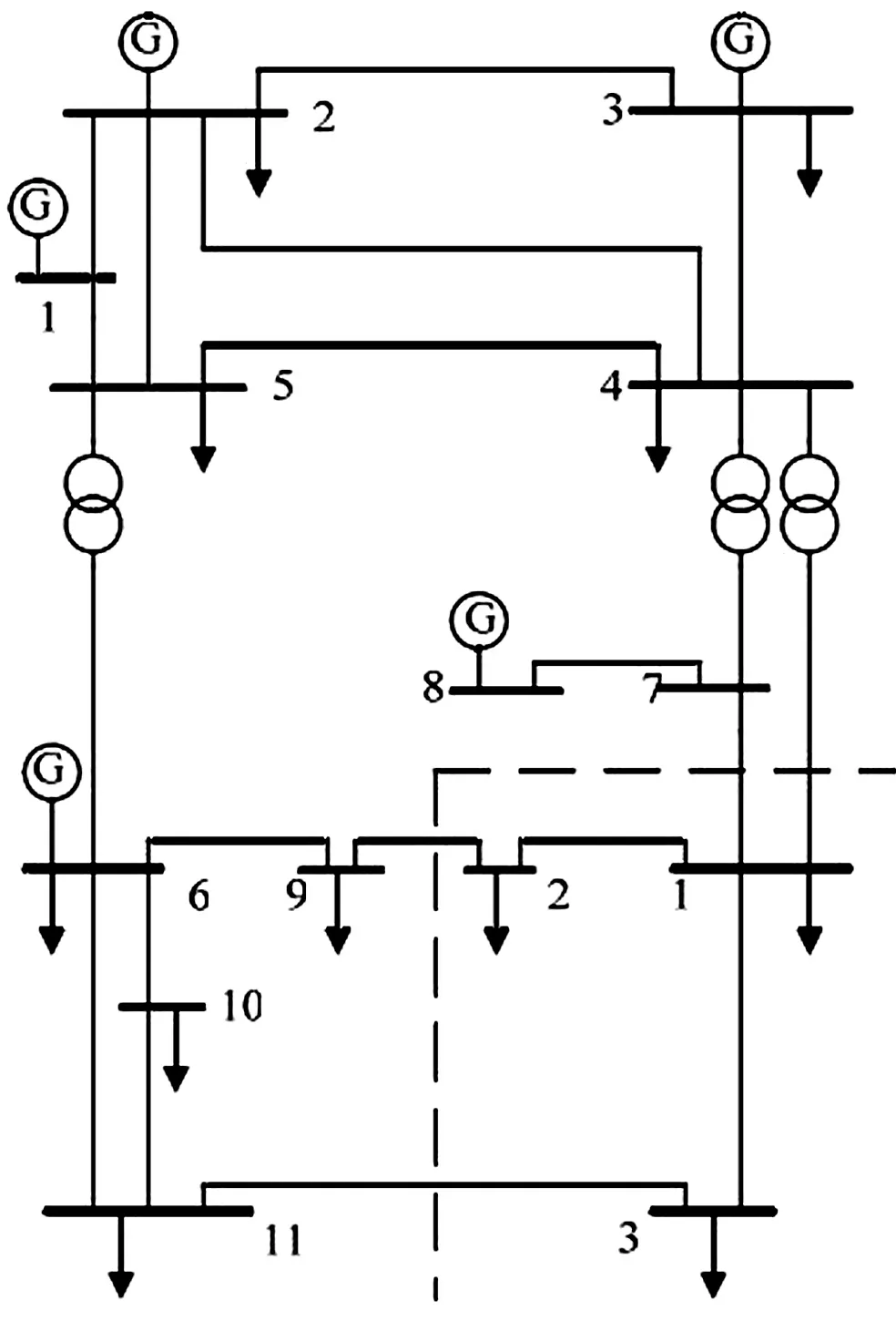
图2 IEEE14节点系统模型接线图

为了验证本文算法的有效性，将其应用于IEEE14节点模型并进行仿真分析，IEEE14节点系统接线图如图2所示，总计70个量测数据，选RN和ΔZ作为特征向量。

在EGSA-FCM算法中，设置种群数maxt为30，万有引力常量初值G0为100，最大迭代次数为30，同时设置模糊聚类中m的值为2，最大迭代次数为100，ε=10-5，初始分类矩阵的选择为当γN≥2.81时，取不良数据集隶属度μA=0.85，良数据集隶属度μB=0.15反之μA=0.15,μB=0.85。

1)量测量中多不良数据存在特征相近

在节点5处，设置注入有功功率P5的不良数据为ΔP5=20 MW，其量测量编号为5，在节点1和节点2间的无功潮流设置不良数据ΔQ12=30 MW，其量测量编号为15，其他量测量设置服从正态分布N(0.1)的随机干扰。检测结果如表1所示。

表1 不良数据检测结果1

2)量测量中多不良数据特征差异较大

在节点5的注入有功功率处设置不良数据为ΔP5=10 MW，其量测编号为5，在节点4的注入无功功率Q4的不良数据为ΔQ4=30 MW，其量测编号为38，在节点4和节点5之间的无功潮流设置不良数据ΔQ4-5=25 MW，其量测编号为55，其他节点设置服从正态分布N(0,1)的随机噪声扰动。检测结果如表2所示。

由检测结果可以看到，当量测数据集中有数据特征迥异的不良数据存在，导致最优聚类数目大于2时，本文方法成功得到最佳聚类结果，最佳聚类数目的为K=3，在该聚类数目下得到的聚类有效性指标值为VCOS=3.328，该值明显优于其他聚类数目下的有效性指标值，算法最终检测辨识出多个不良数据为5号、38号和55号量测。

表2 不良数据检测结果2

4.2 大庆某区域电网

图3 某地区电网变区

大庆某区域电网中，龙新变经由双回线为胶北变和胶南变供电，胶北变下面带有北一变，北六变，北三变，胶南变下面带有南三变，南九变，南四变，南十二变，南十三变，同时变电站下继续带有负荷。其线路图如图3所示。

以该地区电网SCADA系统实时量测数据进行试验测试，选取已经过了数据预处理的部分节点量测数据，包括11座变电站，总计72个测量值，对每个节点和线路有功和无功功率量测值进行了标号。试验中，选择胶北变至北六变支路有功功率量测(量测量编号为40)、北三变注入节点有功功率量测(量测量编号为6)、南九变节点注入有功功率量测(量测量编号为10)三处量测数据设置为不良数据，对其设置超过正常值20%但少于30%的不良数据。经过基于EGSA-FCM算法不良数据检测辨识，检测结果如表3所示。

在设置K=3的聚类数目下，聚类有效性检验指标VCOS=2.761，其数值明显优于其他聚类数目下的有效性检验指标值，最终成功获得的不良数据为第6,10,40号量测。同时可以较为明显地看到在聚类数目K=2和K=4时，检测结果出现误检的情况，在聚类数目K=5时，量测6和量测40分别为北三变注入节点有功功率量测(量测量编号为6)和胶北变至北六变支路有功功率量测(量测量编号为40)，量测量存在明显的相关性，导致残差淹没而发生漏检和误检的情况。

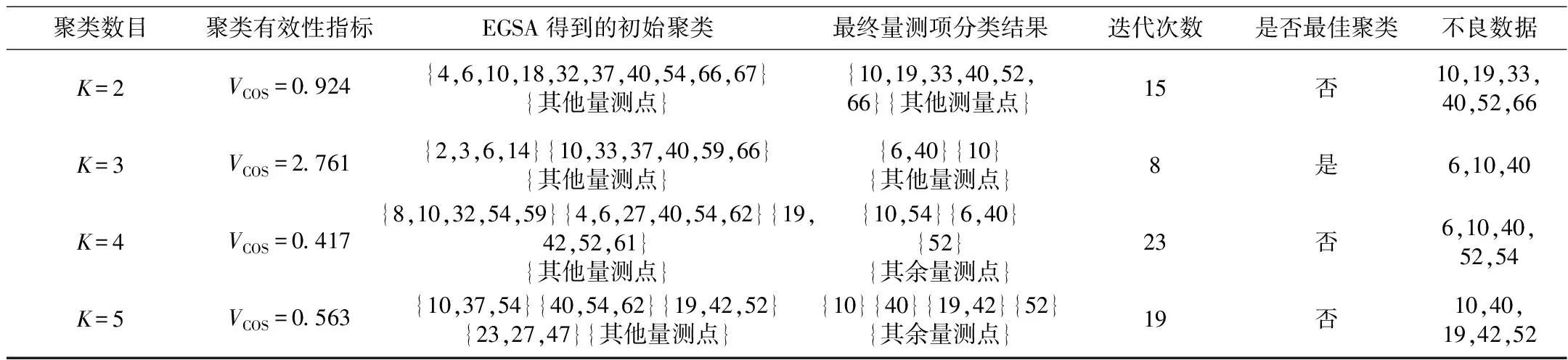
表3 不良数据检测结果3

5 结束语

本文首先提出了增强型万有引力搜索算法，采用改进的速度更新方式和万有引力常量更新方式，大大提高了万有引力搜索算法的搜索性能，针对传统FCM算法对初始化敏感的问题，提出了基EGSA-FCM算法的电力系统不良数据检测辨识的新方法，采用增强型万有引力搜索算法先期搜索，为模糊聚类提供较好的初始解，提高了聚类效果，采用COS有效性指标判定最佳聚类数目，得到最佳聚类结果，最后将其应用到IEEE14节点电力系统和大庆某区域实际电网中，仿真结果表明了本文方法的有效性。