双超声波干涉偏移法测量流体流速
2019-01-30陈水桥王宙洋
陈水桥, 郑 远, 王 鲲, 王宙洋, 何 亮
(浙江大学 物理学系, 浙江 杭州 310027)
常见的流体流速测量方法有:流体通过孔板产生微压差法测量流体流速,优点是实现方法简便,缺点是测量受外界干扰比较大;热线法测量流体流速,利用了热线电流与流速的关系,优点是直观,缺点是仪器调节比较繁琐,误差较大;多普勒频移法测量流体流速,需要测量粒子的速度,实现难度较大[1]。除此之外,超声流量计也是一种比较好的测量流体流速的方法,它常利用波束偏移法、相关法、噪声法等实现流量测定。超声波具有频率高、方向性好、抗干扰能力强等特点,所以在许多科技领域都起到了重要的作用。在大学物理实验教学中,利用超声波的干涉可以精确地测量空气中的声速[2]。在工业应用中,超声波也可以用来测量风速和流体流量。常见的超声风速仪一般基于时差法(包括相位差、频差等)来实现[3-5]。其中,传统的波束偏移法是基于单个超声波波源下,利用两个接收器收到的信号强度的差异来计算发射器发出的波束偏移角,进而推算出介质的流速[6],这种方法适用于流体流速较大的情况,但在低流速情况下,其测量灵敏度低,测量误差较大,而且响应慢,抗干扰能力也弱。本文基于两个超声波波源的双超声波干涉原理,并利用介质流动造成的偏移效应测量流体流速。为了提高测量精度,还用计算机模拟和分析了流体流速和超声波信号强度的关系,并利用CASSY Lab系统平台对气体的流速进行了测量。双超声波干涉偏移法在测量流体低流速情况下具有优势,而且其对多变的流速响应较快,测量数据获得的时效性也较强。
1 双超声波干涉偏移原理
1.1 干涉方程
如图1所示,设有两个发射正弦波的相干波源(超声换能器)S1和S2,在距其所在直线距离为L的位置有一个接收器R,W为通过流体介质的玻璃管道,图中u为流体流速。L1、L2分别为两个相干波源到接收器的距离,d为两波源的间距,x为接收器横向中心轴和两波源对称轴的位移。
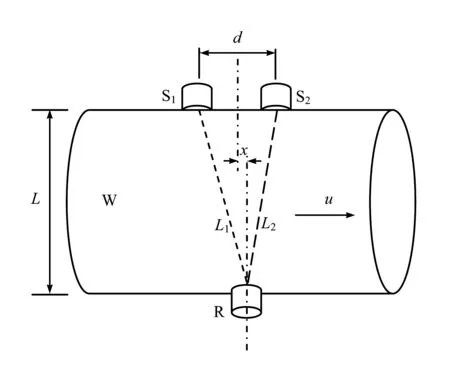
图1 双超声波干涉偏移法原理示意图
两相干波的振动方程分别为
y1=A1cos(ωt+φ0)
(1)
(2)
其中,v为波速,f为波频率,ΔL为两束波到接收器位置的波程差(ΔL=|L1-L2|),根据图1可以推导出:
(3)
由于波源的方向性和超声波在传播中的衰减,A1、A2一般随方向角和距离变化。则在该点的合振动强度有效值为
(4)
考虑积分时间T远大于振动周期,有:

(5)
其中ΔL由(1)式给出。
1.2 计算机模拟与分析
对(5)式代入初始条件(原型实验的环境变量,下同),并固定A1和A2,用Wolfram Mathematica作出I~x的图像如图2(a)。对该图中第一极小值处进行放大(局部范围内可认为A1、A2变化不大),当A1和A2取不同比值时可得图2(b)—(d)。从图中可以看出,无论两者比值如何,在极小值点两侧均有一段区域线性度较高。对图2(b)、(c)两种情况求出I的导函数,得到图2(e)、(f)。
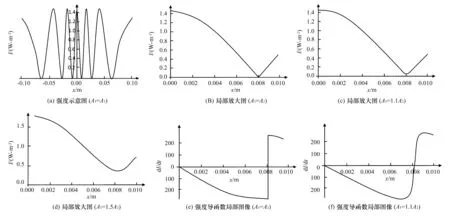
图2 信号强度随位移变化的模拟图像
由计算机模拟和分析可知,在零级两侧线性度较高。
1.3 波束偏移效应
当介质以垂直于发射器、接收器正对方向的速度u流动时(见图1),其携带的声波将发生漂移,设漂移距离为Δxi,则
(6)
其中si为一束声波i从发射器到接收器的传播距离。当u≪v时,可以忽略si的变化。
当接收器位于x位置时,(6)式可写成
(7)
如果x和d比L小一个数量级及以上,则可以认为Δxi和x无关,即
(8)
在接收器所在的横向直线上,这表现为干涉图像的漂移,且漂移距离和介质流动速度u成正比。
2 近似方程和测量方案
2.1 近似方程
在实际测量时,如果信号和被测量存在或近似存在线性关系,将大大降低系统设计和使用过程中的复杂程度。由前述的讨论可知,可以选择第零级两侧线性度较高的区域作为工作区间。由于x≪d,此时(3)式近似为
(9)
代入(5)式得到
(10)
在A1、A2相差不大的情况下,令A1=A2=A,可以进一步简写
(11)
设无气流时的接收器位置为x*,称为工作点。设I的第一极小值点对应位置为xm。取
(12)
线性近似的工作方程可以表示为
(13)
取工作方程斜率:
(14)
流速和信号强度的关系为
(15)
2.2 测量方案分析
当前条件下介质中的声速需要事先测量得到,本文利用CASSY Lab系统平台测得。另外,温度变化会导致声速变化。考虑空气和气温对声速变化起主要作用。一般来说,对于1个标准大气压、50%湿度、0.04%的CO2浓度的空气[7],15℃和35℃的声速误差为3.7%。对于液态水,根据J.Lubbers等的经验公式计算[8],15℃和35℃ 的声速误差为3.6%。所以在精度要求不高的工业应用中,可以不予考虑[9]。但在精度要求较高的场合下,需要对(15)式中的声速v进行温度修正,即
(16)
为了简化测量,本文在实验时保证了在恒定温度下测量,所以,在计算时不考虑温度的影响。
3 实验与分析
3.1 仪器系统
仪器系统主要包括CASSYLab系统平台、80W离心风机和816型风速计,其中CASSYLab系统平台主要由控制器、信号发生器、放大器和换能器等仪器组成。图3为整个仪器测量系统示意图。
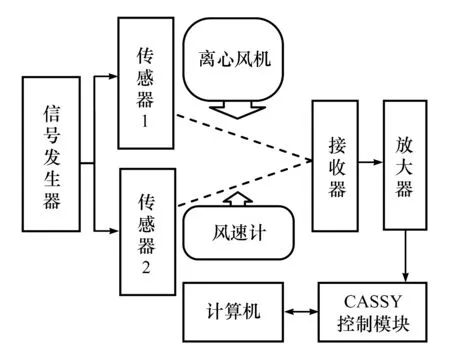
图3 仪器系统布局示意图
3.1.1CASSYLab
CASSYLab系统是Leybold公司开发的、支持CASSY系列传感器和采集模块的软件。通过CASSYLab软件可以直接测量发出和接收声脉冲的时间差。将计算机的串行通信接口与CASSYLab系统采集模块连接,就可利用CASSYLab系统中的传感器自动采集实验数据。同时,还可用该软件对数据进行实时处理。极大地方便了实验的数据测量与处理。
3.1.2 主要参数
实验中主要仪器参数及环境数据见表1。

表1 主要参数
3.2 实验与分析
3.2.1 实验设计
在无风情况下,先测量接收器所在直线上的信号强度最大值,即零级峰值ymax,并在信号发生器无输出的情况下测量背景噪声ydark(0)。调整接收器位置,使干涉强度约为峰值一半,测量信号记为ysig(0)。启动离心风机,以不同转速使换能器间的空气基本匀速流动,分别测量信号发生器有输出或无输出下的接收器信号强度ysig(u)和ydark(u),并用风速计测量空气流速umeas,并确定误差umeasEr(考虑测量误差以及风速计标称准确度)[10-11]。在空气流速为u的情况下,净干涉强度(以电压表示)为
(17)
零级峰值强度为
γmax=ymax-ydark(0)
(18)
3.2.2 实验结果
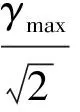

表2 实验数据
空气流速u和风速计测量空气流速umeas曲线图见图4。
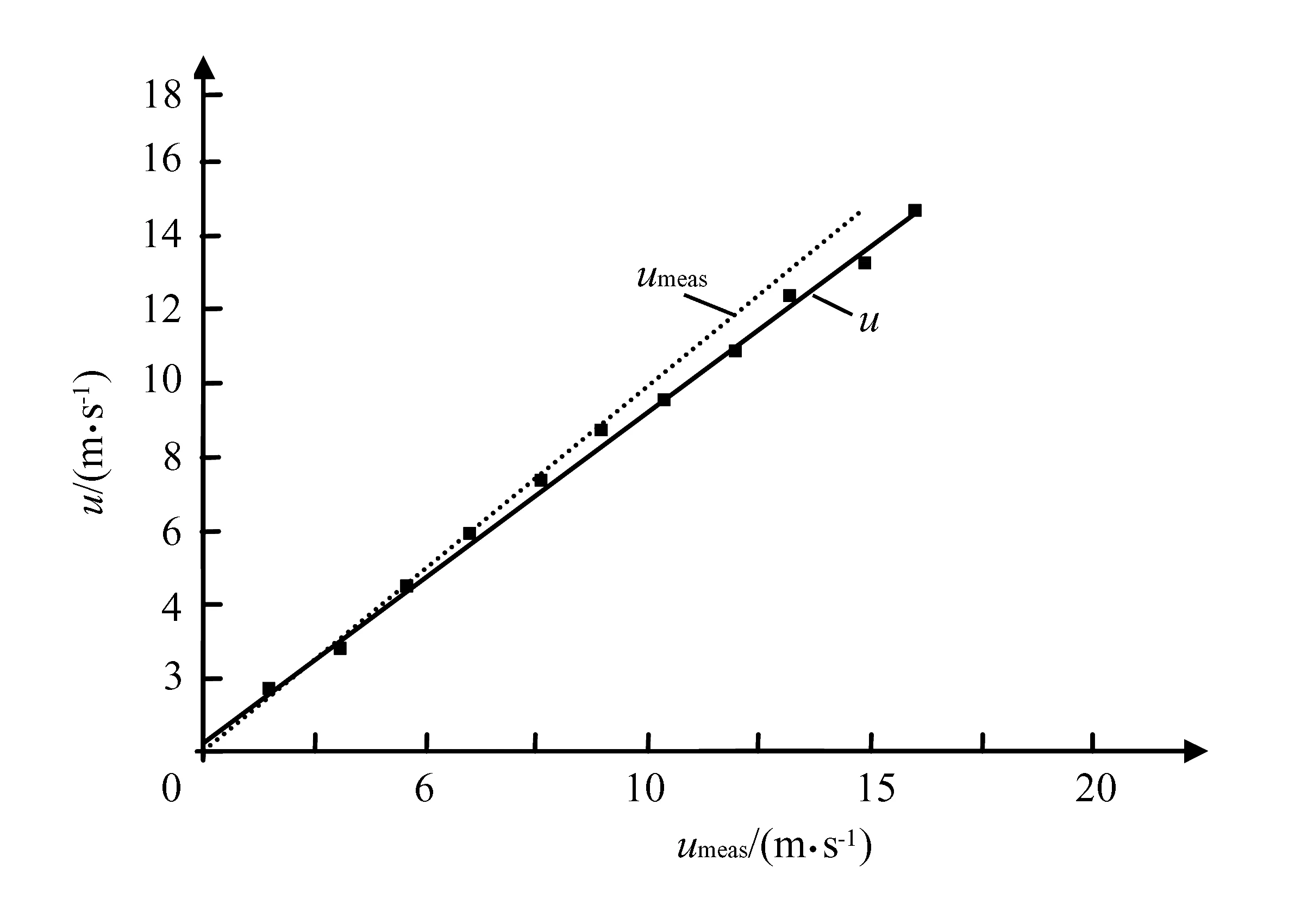
图4 流速比较
由式(15)计算得出的空气流速u和用风速计测量空气流速umeas比较曲线图可见,两者测得的数据基本吻合。平均相对误差为5.5%。
3.2.3 误差分析
本实验的主要误差来源于所使用的标定仪器,尤其是816型风速仪,其测量头体积较大(转叶式设计),影响灵敏度[12-13]。实验中对不同风速进行了多次测量,获得了比较理想的数据,并采用了多次测量取平均值的方法来减小风速测量带来的误差。
实验中,风机刚刚开启时会产生一个频率约为18kHz的明显的噪声信号,随着风速变大,该信号频率变化不大。由于测量流速通常不需要让换能器间隔很大距离,超声波在介质中传播的衰减不明显,故采用更高频率的换能器将有助于减小误差。
实验的另一个误差来源于CASSYLab系统平台的硬件条件,本文采用的是40kHz的超声换能器。在管道中,40kHz左右的环境噪声最强[14]。虽然本实验中各组数据已经减去了相应的环境噪声强度,但是噪声对超声波干涉波形产生的影响是无法消除的[15]。为了减小这些误差,实验中利用宽拾音范围的麦克风和示波器,在切断换能器信号源的情况下对风道噪声进行了定性测定。
4 总结
利用双超声波干涉偏移法测量流体流速系统具有以下特点:方法简单、测量响应快,能测量低流速下的流体介质的流速;实验数据表明,推导出的近似公式的线性度较高。如果需要进一步扩大测量范围,则可以对数据进行非线性拟合,这将是下一步研究的重点。另外,本系统以换能器输出电压为被测量,故其绝对误差不受风速的限制。一定范围内流速和电压的关系可以作线性近似处理。本装置已经申请到国家发明专利。
