基于EKF的PMSM无传感器控制研究
2019-01-30季传坤钱俊兵
季传坤,钱俊兵
(昆明理工大学机电工程学院,云南 昆明 650500)
0 引言
永磁同步电机(permanent magnet synchronous motor,PMSM)具有结构简单、体积小、效率高、响应快、调速范围宽等优点[1],被广泛应用于国防、航空航天、工业控制、农业生产等领域。但PMSM的永磁体所用材料价格昂贵,大大限制了PMSM的发展。随着永磁体材料汝铁硼的出现,PMSM进入一个全新的发展时期。PMSM通常采用磁场定向矢量控制,控制系统需要安装机械传感器来测量转子的位置和电机转速。然而,安装高精度的机械传感器不仅会增加电机的成本,且不能保证在复杂状态下的测量精度和准确度[2]。因此,PMSM无位置传感器控制成为研究的热点[3]。PMSM无位置传感器控制常用的方法有:状态观测器、模型参考自适应、高频注入、智能控制等[4]。
模型参考自适应算法虽然控制方法比较简单,但是辨识的位置和速度以及控制系统的工作效率主要取决于参考模型能否得到准确的参数[5]。高频信号注入法适用于凸极比较高的电机,且高频响应和相位延迟对算法精度的影响很大[6]。智能控制算法,如神经网络、遗传算法等[7-8],算法比较复杂,实现较为困难。本文提出的扩展卡尔曼滤波(extended Kalman filter,EKF)控制方法具有较强的自适应性和抗干扰性,且操作简单易行。仿真结果表明,本文提出的基于EKF控制的无传感器控制方法具有很好的抗负载性和系统响应性。
1 PMSM矢量控制数学模型
矢量控制又称磁场定向控制。其基本思想是:模拟直流电机的控制方法,利用坐标变换将PMSM的定子电流分解成励磁电流分量和转矩电流分量(两个彼此相互垂直的分量),实现励磁分量和电磁转矩分量的解耦控制,完成对电机的磁链和电流的单独控制[9]。PMSM矢量控制方法有:id=0控制、cosφ=0控制、最大转矩电流比控制和弱磁控制。因id=0控制方法控制系统简单且转矩性好,故本文采用id=0控制方法。
基于id=0永磁同步电机矢量控制框图如图1所示。

图1 基于id=0永磁同步电机矢量控制框图
由图1可知,基于id=0的矢量控制方法是双闭环控制。其中:电流环为内环,转速环为外环。转速环中电机反馈转速n和电机给定转速nret的误差,经PI控制器获到q轴给定电流iqref。在电流环中,CLARK变换将电机的三相电流Ia、ib、ic转变为αβ轴电流iα、iβ;然后再经PARK变换得到轴反馈电流id、iq、dq电压。udref、uqret是dq反馈电流分别与电机的给定电流0、iqref的误差经PI控制器得到的。经过PARK逆变换之后,获得α、β轴电压uαref、uβref,并且由空间矢量脉宽调制(space vector pulse width modulation,SVPWM)模块产生脉宽调制(pulse width modulation,PWM)波以驱动逆变器,进而由逆变器产生三相电压驱动电机并输出三相电流,从而形成闭环控制。
αβ坐标系下表贴式PMSM的电压方程为:
(1)

(2)
式中:Rs为相电阻;L为相电感;ω为电机转子电气角速度;φf为永磁体磁链;θ为电机转子电气角度。
2 EKF算法的原理
卡尔曼滤波是一种递推计算方法,它是在线性最小方差估计基础上发展起来的,并且还是一种线性系统的随机观测器[10]。其基本思想是利用观测数据对状态变量的预测估计进行修正,以得到状态变量的最优滤波估计,即最优滤波估计=预测估计+修正[11-12]。EKF算法是线性系统状态估计在非线性系统的扩展应用。
EKF的状态估计可分为两个步骤,即预测和校正。具体运算流程如下。

(3)
式中:Ts为采样周期。

TsF(k)T]+Q
(4)
③计算EKF的增益矩阵K(k+1):
(5)

(6)


(7)
3 基于EKF的永磁同步电机实现
离散化的卡尔曼滤波模型为:

(8)
式中:x(k)、y(k)、u(k)分别为系统状态变量、输入矢量和输出矢量;V(k)为系统噪声;W(k)为测量噪声。
系统噪声主要包括系统参数误差、模型误差及扰动信号等。假设V(k)和W(k)均为值为零的高斯白噪声,其协方差为:
(9)
由式(1)、式(2)可得基于EKF的电机模型为:
(10)
其中:x=[iαiβωθ]T;u=[uαuβ]T;y=[iαiβ]T。
(11)
(12)

(13)

(14)
(15)
式中:P为电机极对数;ωm为电机的机械角速度,rad/s;n为电机转速,rad/min。
4 仿真分析
为了验证EKF算法的可行性,本文搭建了基于MATLAB/Simulink的PMSM仿真模型。仿真所用表贴式PMSM的具体参数为:电机额定转速n=3 000 rad/min,额定转矩TL=2.4 N·m,定子相电感Ld=Lq=L=6.552×10-3H,定子相电感Rs=0.901 Ω,转子永磁体磁链φf=0.038 4 Wb,转动惯量J=1.2×10-4kg·m2,极对数P=4,阻尼系数B=0。
基于EKF的PMSM无传感器控制系统如图2所示。

图2 基于EKF的PMSM无传感器控制系统图
由图1和图2可知,基于id=0的矢量控制方法和基于EKF的无传感器控制方法的不同点是:基于EKF的无传感器控制方法是将αβ坐标系下的电流和电压作为输入变量,经过EKF算法估算出转子转速和转子位置的数值,取代了基于id=0的矢量控制方法中的转速和位置(机械)传感器。



电机在空载条件下,电机转速由100 rad/min变化到1 600 rad/min的仿真结果如图3所示。
由图3(a)和图3(b)可知,在转速上升阶段实测与估计转速误差比较大,最大转速误差为100 rad/min。但随着EKF算法的推进,转速误差慢慢减小,电机趋于稳定状态,估计转速与实际转速曲线基本重合。由图3(c)和图3(d)可知,随着电机转速误差的减小,转子位置误差也慢慢变小,进一步证明了EKF算法具有收敛性。

图3 PMSM空载仿真结果
电机在负载条件下,电机转速由100 rad/min变化到1 600 rad/min的仿真结果如图4所示。
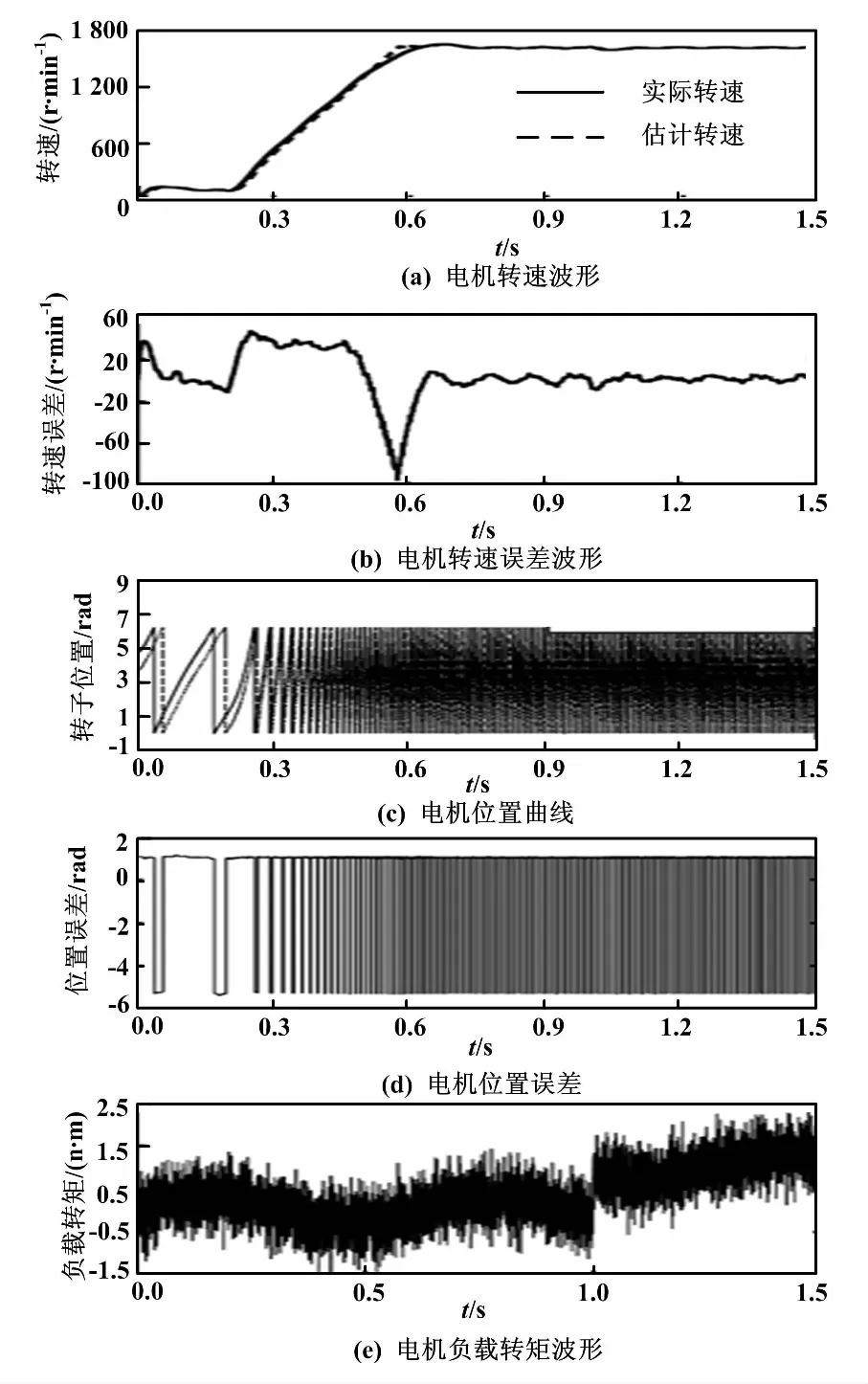
图4 PMSM负载仿真结果
由图4(e)可知,负载值是随机变化的,并在t=1 s时对电机突加负载TL=1 N·m。由图4(a)和图4(b)可知,电机在负载情况下,EKF算法依然能准确的估算出电机的转速。在1 s时给电机突加负载,转速值存在波动,但在0.08 s内恢复到稳定状态,证明EKF算法有较强的抗干扰能力。由4(c)和图4(d)可知,在负载状态下,转子估计位置和实际位置误差在电机到达稳定状态后也逐渐较小。由图3和图4可知,转速误差值和转子位置误差值并没有在负载状态下有太大的波动,证明EKF算法有一定的收敛性和抗负载性。
5 结束语
本文在PMSM矢量控制的基础上,提出了一种基于EKF的PMSM无传感器控制方法,并利用Matlab /Simulink 仿真软件进行了仿真分析。仿真结果表明,该控制方法在电机随机负载和空载情况下均能准确地估算出电机的转速和转子位置。虽然在电机启动阶段误差较大,但是由于EKF算法的收敛作用,误差快速减小,电机在较短时间内恢复到稳定状态。在电机突加负载的情况下,该算法也具有较好的抗负载性和系统响应性。
