直流电机控制系统性能评价及控制优化

辛悦夷，李奇达

(1.东北大学信息科学与工程学院，辽宁 沈阳 110819；2.东北大学流程工业综合自动化国家重点实验室，辽宁 沈阳 110819)

0 引言

随着现代工业的不断发展，工厂中的控制回路越来越多。一个控制系统由许多回路组成。这些控制回路数量庞大，而且在运行一段时间后，由于运行过程中操作条件的改变、过程的非线性和机器设备故障等原因，会使得控制系统性能下降。因此，对控制系统进行性能评价，并对控制器进行优化非常必要。

单输入单输出(single in single out,SISO)回路则是系统中典型的控制回路。Harris提出的最小方差算法能够估计回路的最小方差基准值[1]。该方法只需知道控制系统的运行数据和被控过程的时延知识，不要求掌握控制过程的模型，因此在工业上得到了广泛的应用。同时，利用极点配置技术来矫正线性系统的动态响应特性，是现代控制领域研究较多的问题之一。开环周期系统能够用一组合适的状态反馈，实现闭环单值性矩阵特征值的任意配置。本设计讨论了具有时变状态或者输入维数的线性离散周期系统的极点配置问题，并利用存在于状态反馈增益个数中的自由度，实现了鲁棒极点配置。利用状态观测器，将所测量到的输出量和控制量重构出全部状态。本设计中采用预报观测器，利用输入量及模型参数进行预报。观测器的极点配置使状态重构具有较快的跟踪速度。利用Ackermann公式计算出状态反馈控制规律L和观测器增益矩阵K。采用Z变换，计算出状态观测器模型，从而完成系统设计。

1 控制系统性能评价

1.1 控制系统性能评价步骤

对控制系统进行性能评价，可以分为以下步骤[2]。

①采用相关性分析法得出系统时延d。

将最小方差估计值与输出方差实际值相除，获得系统的性能评价指标。

1.2 单输入单输出控制系统最小方差准则

SISO控制系统框图[3]如图1所示。

图1 SISO控制系统框图

由图1可知，系统输出为：

(1)

将扰动传递函数采用丢番图方程展开，此时系统输出可改写为：

Fat+Lat-d

(2)

由于白噪声是相互独立的，所以对等式两边同时取方差；可以看出，当且仅当L=0时，系统的输出方差达到最小值Var(Yt)=Yar(Fat)。此时，可得单回路最小方差控制规律为：

(3)

此时，系统输出为Yt=Fat。由于F与控制器的传递函数Q无关，因此Fat不随控制器参数的变化而变化，也就是最小方差控制下单变量控制系统的输出。根据最小方差控制性能评价思想，定义经典的Harris性能指标为：

(4)

(5)

1.3 SISO控制系统性能评价算法研究

由图1可得输出表示式为：

(6)

可将等式右边第二项表示为一个阶次为m的自回归模型，则式(6)可表示为：

Yt=Fat+φ1Yt-d+φ2Yt-d-1+…+φmYt-d-m+1=

(7)

记录下系统的闭环输出数据，并将其表示为矩阵形式：

Y=Fat+XΦ

(8)

其中：

Φ=[φ1φ2…φm]T

由最小二乘法，可得参数估计值为：

(9)

则系统的最小方差估计值可表示为：

(10)

系统的输出方差实际值为：

(11)

则系统的性能评估指标[4]为：

(12)

2 直流电机的物理模型、参数及设计要求

2.1 物理模型

本设计的被控对象所采用的是直流电机，实现闭环调速控制器的设计。其物理模型[5]如图2所示。

图2 直流电机物理模型

双闭环控制电流调速系统的特点是电机的转速和电流分别由两个独立的调节器控制，且转速调节器的输出就是电流调节器的给定。因此电流环能够随转速的偏差调节电机电枢的电流。当转速低于给定转速时，转速调节器的积分作用使输出增加，即电流给定上升，并通过电流环调节使电机电流增大，从而使电机获得加速转矩，电机转速上升。当实际转速高于给定转速时，转速调节器的输出减小，即给定电流减小，并通过电流环调节使电机电流下降，电机因为电磁转矩减小而减速。当转速调节器饱和输出达到限幅值时，电流环以最大电流限制实现电机的加速，使电机的启动时间最短。

调速系统原理框图[6]如图3所示。

图3 调速系统原理框图

2.2 电机参数

电机参数如下。

①电机型号：DJ15。

②额定参数：PN=185 W,UN=220 V,IN=1.2 A,n=1 500 rad/min,λ=1。

③电枢电阻R=25.714 3 Ω，电枢电感L=0.734 7 s。

④电机飞轮惯量：GD2=0.10 N/m2。

⑤电枢回路电磁时间常数TL=0.032 8 s，系统的机电时间常数Tm=0.08 s，电动机电势时间常数Ce=0.114 7 s，转矩常数Cm=1.095 3 N·m/A。

⑥电流反馈系数：β=4.615 V/A。

⑦转速反馈系数：α=0.04 V/(r/min)。

2.3 设计要求

设计控制器，使得系统的单位阶跃响应性能指标为：

①调节时间小于0.2 s；

②系统超调量小于2%；

③无稳态误差。

3 直流电机模型建立及特性测试

直流电机转矩和电枢电流的关系为：Tr=Cmi。电枢旋转产生反电动势e与旋转运动角速度ω的关系为：e=Kεω=Cen。根据牛顿第二定律，可得运动平衡方程式[7]为：

(13)

式中：b为电机摩擦系数，此处忽略不计。

根据回路电压法，电机电枢回路方程式为：

(14)

(15)

式中：m为一个旋转体上的一个质点的质量，为质量G和重力加速度g之比；R和D分别为旋转体的半径和直径。

电机电枢回路电压平衡和电机运动平衡的一组微分方程式[8]为：

(16)

(17)

设系统的状态变量为x1=i,x2=n。以输入电压u为输入、转速n为输出，可得状态空间表达式为：

(18)

代入系统参数，可得：

当设置给定电压是220 V时，系统阶跃响应曲线如图4所示。

图4 系统阶跃响应曲线

由图4可以得出：最大峰值转速为2 012 rad/min，稳态值为1 920 rad/min，所以原系统的超调量为4.79，调节时间Ts=0.237 s。

对系统进行能控性判断与能观测性判断：

由此可知，系统是完全能控能观测的。因此，求出原系统在空载的情况下超调量为4.96%，调节时间(2%的误差带)Ts=0.228 6 s，系统的稳态误差Ess为0.1%。

从以上数据计算结果可得，系统并不满足设计指标。所以，有必要设计一个状态观测器来修正原系统，使新系统指标达到所要求的设计指标。

4 基于状态空间模型的直流电机控制器的设计

4.1 期望配置极点的确定与状态观测器的设计

根据上述设计指标要求，选择调节时间(2%的误

x1,2=-22.45±18.074

z1,2=-0.035 25±j0.146 92

4.2 建立离散的状态空间模型

使用MATLAB语言，将连续状态空间模型转化为离散的状态空间模型。使用[F G] =c2d(A,B,0.1)命令，可得：

由z1,2求出αc(z)=z2+0.049 4z+0.011 11，分别利用如下公式求出反馈控制率矩阵L、状态观测器反馈增益矩阵K、前馈增益矩阵Lr：

L=[0 … 1] [GFG…Fn-1G]-1αc(F)

(19)

(20)

(21)

将以上各式代入控制器的模型表达式中：

同时，利用Z变换求出x1(z),x2(z)，结果分别为：

x1(z)=[-0.001 4x2(z)+0.012 5uz)-0.000 3(y(z)-

x2(z)=[37.698x1(z)+7.707 4u(z)-0.089 1(y(z)-

u(z)=0.538 3x1(z)-0.006 0u(z)+0.108 7r(z)

根据上述参量之间的关系，建立Simulink仿真框图，整理成传递函数的形式，如图5所示。

图5 传递函数形式的仿真框图

当给定阶跃信号为1、H(1)=1及加上增益时系统阶跃响应曲线如图6所示。

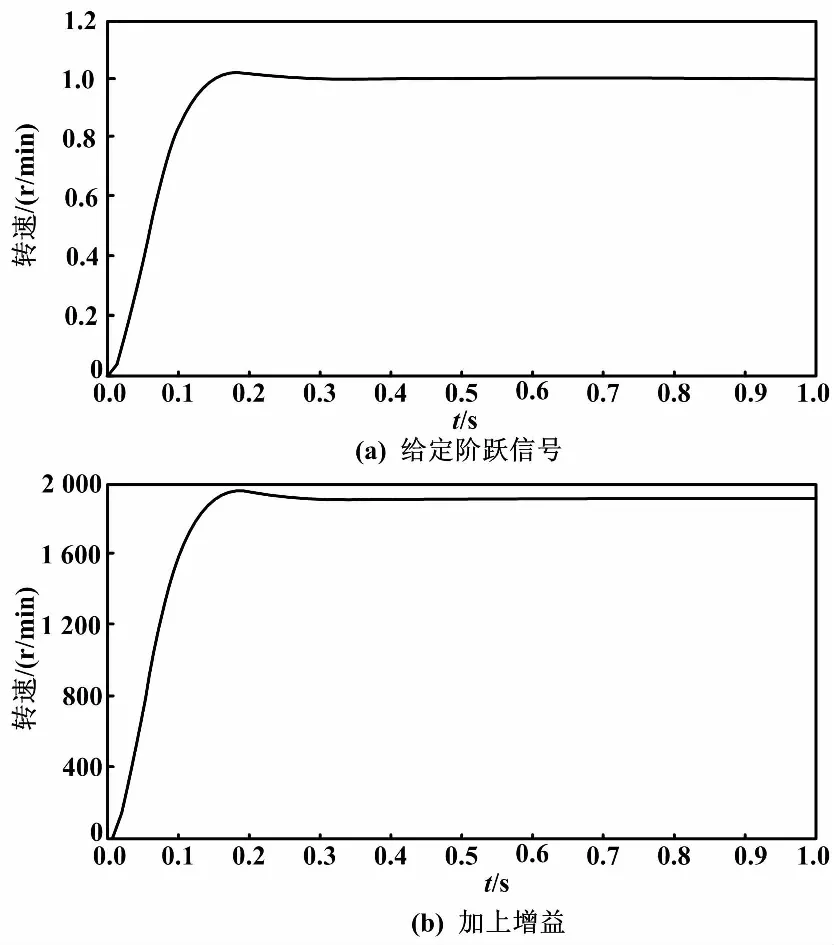
图6 系统阶跃响应曲线

由图6可得出：最大峰值转速为1 955 rad/min，额定转速为1 918 rad/min，所以超调量为1.93%，满足设计要求。系统到稳态值的时间为0.31 s，所以调节时间满足设计要求。稳态转速为1 918.16 rad/min，额定转速为1 918 rad/min，所以稳态误差Ess<0.01%，满足设计要求。

由以上分析可知：三项指标均满足设计要求，说明极点配置合理。与原系统相比，新系统的超调量更小，响应时间更快，系统稳定性更好。

5 基于传递函数的电动机控制器设计

5.1 设计原理

基于传递函数模型设计控制器。采用传递函数的多项式计算来代替状态空间模型的矩阵形式计算。在上述讨论中，采用的方法是前馈与反馈相结合的跟踪系统控制结构[9]。首先，根据被控对象的状态空间模型，采用极点配置的方法分别设计观测器和控制规律[10]。然后，根据分离性原理，组成控制器。最后，将其写成传递函数的形式，得到由前馈控制器和反馈控制器组成的复合控制器。

5.2 计算R(z)和S(z)

5.3 建立极点配置复合控制器模型

极点配置复合控制器模型如图7所示。

图7 极点配置复合控制器模型

当给定信号为220、H(1)=8.718时，仿真结果如图8所示。

图8 系统阶跃响应曲线

5.4 分析

根据上述讨论的结果仿真分析得知，前馈控制器与反馈控制器建立的模型和基于状态空间模型设计得到的结果基本相同。这就说明基于传递函数模型和基于状态空间模型设计得到的控制器具有一致性。

6 结束语

本文首先对控制系统进行性能评价，通过时间序列分析技术找出反馈不变项，作为性能评价的基准值，从而得出性能评价指标。本设计中采用两种方法对直流电动机的模型进行设计闭环调速系统控制器，分别为基于状态空间模型极点配置的控制器设计和基于传递函数模型的复合控制器的设计。通过MATLAB仿真并对两种设计方法进行比较，可知在控制性能上两种方案能够达到完全一致的效果，满足设计要求。随着现代工业的不断发展，工厂中的控制回路越来越多。在实际的工业过程中，工况会随着时间的推移而发生变化，此时，原控制器已无法满足当前系统的控制要求，会使得系统的控制性能大幅度下降，不仅导致产品质量随之下降，还可能造成安全事故。因此，对控制系统进行性能评估与优化的研究具有非常重要的意义。