RBF整定 PID在永磁同步电机控制中的应用研究
2019-01-30聂启鹏唐明新
聂启鹏,唐明新
(大连交通大学电气信息工程学院,辽宁 大连 116028)
0 引言
当前,环境问题越来越受到人们的重视。随着社会的发展,传统燃油汽车将逐渐退出历史舞台。如何实现对电动汽车驱动电机的稳定、精确调速控制,已成为各个汽车厂商重点研究的问题之一。交流永磁同步电机启动时间较短、功率密度大、启动转矩较高,因此被大多数汽车厂商用作电动汽车的驱动电机。与直流电机不同的是,交流永磁同步电机具有非线性、耦合性等特性。传统的控制方法是首先对其进行解耦处理,采用比例积分微分(proportion integral derivative,PID)加矢量控制的方法实现调速控制。但是电动汽车的工作环境复杂多变,而且有风阻、负载变化等因素影响。传统的控制方法往往存在较大误差。径向基函数 (radical basis function,RBF)神经网络有很强的非线性函数逼近能力和自学习能力,在系统中可以不断减小因不确定因素导致的误差。因此,本文在电机的控制中引入了RBF神经网络,利用参数线性化的方法来实现对被控对象不确定参数的辨识,并根据被控对象的参数变化情况随时调整网络权值。RBF神经网络具有良好的抗干扰能力和自适应能力。
1 PID参数整定及应用
从经典控制理论、现代控制理论到目前的智能控制理论,自动控制领域出现了很多先进的控制算法。在此过程中,PID控制因其结构简单且控制效果良好,在控制系统中得到广泛应用[1]。设计PID控制器的核心内容是根据被控对象的特性确定它的比例系数、积分时间和微分时间。在线性系统中,PID控制相对于其他多数控制算法具有无可取代的优势。即使是稍复杂的非线性系统,在对系统进行简化和线性化之后,PID控制器也能达到比较好的控制效果。
随着科技发展,被控对象变得越来越复杂,传统的PID控制器在实时性和自适应性方面存在欠缺。对此,人们通过整定PID控制参数来实现对非线性系统的控制。电动汽车中,永磁同步电机和其速度控制系统具有明显的非线性和快时变等特点,并且易受外界干扰[2]。针对上述问题,本文提出了RBF神经网络在线自整定PID控制。RBF神经网络结构简单,由输入层、隐层和输出层组成。从输入层到隐层的映射是非线性的,从隐层到输出层的映射是线性的。隐层神经元的变换函数即为径向基函数,其特点是对中心点径向对称且衰减,是一个局部响应函数。因此,采用RBF网络,可大大加快学习收敛速度并避免局部极小问题,能满足实时控制的要求[3]。
2 永磁同步电机数学模型
永磁同步电机由永磁体作为转子。通过永磁体励磁产生同步旋转磁场,三相定子绕组在旋转磁场的作用下通过电枢反应,感应三相对称电流。要实现对这样一个复杂矢量系统的调速控制,首先要将矢量系统通过坐标变换的方法等效为类似于直流电机的简单标量系统,获得像直流电机一样的良好动态和静态特性[4-5]。为了便于建立永磁同步电机的数学模型,先作如下假设:①永磁材料的电导率为零;②转子没有阻尼绕组;③忽略铁芯饱和,不计涡流和磁滞损耗;④相绕组中的感应电动势为正弦波。
对于正弦波调速永磁同步电机而言,大多数情况下,转子不存在阻尼绕组,因此电机的电压、磁链和电磁转矩方程在两相旋转坐标系下可分别简化为式(1)~式(3)的形式[6]。
电压方程:
(1)
磁链方程:
(2)
电磁转矩方程:
Te=pn(Ψdiq-Ψqid)=pn[Ψfiq+(La-Lq)idiq]
(3)
在永磁同步电机的控制中,一般取id=0,可以得到电机的转矩方程:
Te=pnΨfi
(4)
永磁同步电机结构如图1所示。
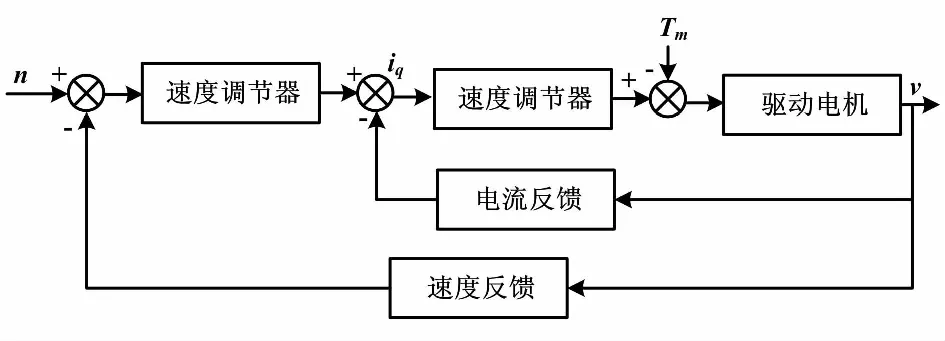
图1 永磁同步电机结构图
在有负载存在的情况下,永磁同步电机的机械运动方程为[7]:
(5)
式中:iq为q轴电枢电流;Te为电磁扭矩;Tm为负载;Kf为扭矩系数;M为电机动子质量;F为黏滞阻尼。
因此得到电流iq、系统速度输出v和负载阻力Tm之间的关系为:
(6)
为了能在Matlab语言中实现对电机的控制,需要得到电机的离散化数学模型。在控制对象的输入侧加入保持恒定值的零阶保持器G(s):
(7)
推得离散化方程:
(8)
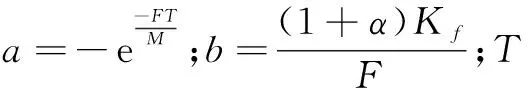
3 RBF神经网络
RBF网络结构如图2所示。RBF网络一般只有三层。其中:输入层和中间层计算输入的x矢量与样本矢量c欧式距离的RBF值,输出层计算线性组合的和。一般取高斯函数作为RBF。

图2 RBF网络结构图
3.1 RBF网络的学习算法
RBF网络的学习算法流程分为以下几个步骤。
(1)基于聚类(K-mean)算法[8],求取基函数中心。
①将网络初始化,随机选取h个训练样本作为聚类中心ci(i=1,2,…,h)。
②聚类算法简图如图3所示。灰色菱形表示选定的聚类中心。由于 RBF 只对选定样本附近的输入有反应,输入的训练样本集合按最邻近规则分组,即圆内的所有菱形为一组。按照输入样本xp与中心点ci之间的欧氏距离,将xp分配到输入样本的各个聚类集合Xp(p=1,2,…,P)中。RBF使样本只被附近圆内的输入激活。

图3 聚类算法简图
③重新调整聚类中心。
通过计算,得到各个聚类集合Xp(p=1,2,…,P)中样本的平均值。该值即为新的聚类中心ci。如果它的值和之前一样,那么所得到的ci就作为RBF神经网络最终的基函数中心;否则,返回步骤②,进入下一轮的聚类中心求解。
(2)求解方差。
取高斯函数作为RBF神经网络的基函数,其方差为:
(9)
式中:cmax为所选取聚类中心之间的最大距离。
(3)如式(10)所示,利用最小二乘法计算得到隐含层到输出层神经元之间的连接权值w:
(10)
RBF网络学习算法流程如图4所示。

图4 RBF网络学习算法流程图
3.2 RBF神经网络逼近非线性函数
为了表明RBF网络在非线性函数逼近上具有独特的优势,给定一个非线性函数Matlab随机产生输入变量x1、x2。建立RBF神经网络后,利用RBF对其进行函数逼近,得到的RBF逼近非线性函数,如图5所示。从图5可以看到,由RBF神经网络[6-12]得到的仿真结果图像与目标函数图像之间存在很小的误差。利用RBF,可以很好地逼近非线性系统函数。

图5 RBF逼近非线性函数
4 RBF网络整定PID
4.1 RBF网络信息辨识
RBF整定PID首先需要利用RBF神经网络对被控对象进行Jacobian信息辨识。在RBF网络结构中,网络的输入向量为X=[x1,x2,…,xn]T。将RBF网络的径向基向量设为H=[h1,h2,…,hm]T。其中,hj为高斯函数:
(11)
网络的第j个结点的中心矢量为:
Cj=[cj1,cj2,…,cji,…,cjn]T
(12)
设网络的基宽向量为:
B=[b1,b2,…,bm]T
(13)
式中:bj为大于零的数。
作为节点j的基宽度参数, 网络的权向量为:
W=[w1,w2,…,wj,…,wm]T
(14)
辨识网络的输出如式(11):
vm(k)=w1h1+w2h2+…+wmhm
(15)
在对永磁同步电机的控制中,辨识神经网络的输入向量为:
X=[v(k),v(k-1),iq(k-1)]
(16)
式中:v(k)和iq(k)分别为速度和电流信号。
RBF辨识器的性能指标函数为:
(17)
网络的输出权值、节点中心值以及节点基宽参数的迭代算法根据梯度下降法计算如下。为了加快J1的收敛,加入了一个动量项,α为动量因子,η为学习速率。
wj(k)=wj(k-1)+η[yout(k)-ym(k)]hj+
α[wj(k-1)-wj(k-2)]
bj(k)=bj(k-1)+ηΔbj+α[bj(k-1)-bj(k-2)]
cji(k)=cji(k-1)+ηΔcji+α[cji(-1)-cji(k-2)]
Jacobian阵(即被控对象的输出对输入控制信息的灵敏度信息)的计算方法为:
4.2 RBF网络PID整定原理
在对比了几种PID控制器后,本文采用增量式PID控制器。其控制误差为:
error(k)=r(k)-v(k)
(18)
PID控制器的三项输入为:
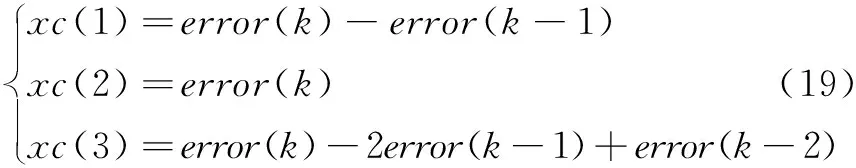
控制算法如式为:
iq(k)=iq(k-1)+Δiq(k)
(20)
Δiq(k)=kp[error(k)-error(k-1)+kierror(k)+
kd(error(k)-2error(k-1)+error(k-2)]
RBF神经网络对PID控制器整定的指标函数为:
(21)
采用梯度下降法,调整kp、ki、kd的变化量:
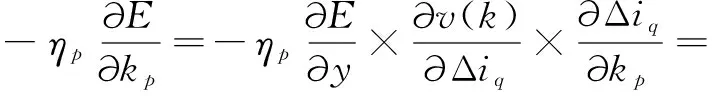
(22)

(23)

(24)
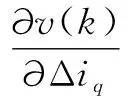
RBF整定PID控制如图6所示[9-12]。

图6 RBF整定PID控制图
5 仿真结果及分析
永磁同步电机参数如表1所示。

表1 永磁同步电机参数表
经过计算,得到的永磁同步电机离散化数学模型:
v(k)=0.5v(K-1)+0.1iq(k-1)-Tm(k-1)
(25)
根据上述算法,用m语言编写出RBF整定PID控制电机的程序。经过反复修改神经网络学习率、神经元个数等参数,优化出一个精确且高效的控制系统。空载状态控制如图7所示。空载状态PID参数整定如图8所示。

图7 空载状态控制图

图8 空载状态PID参数整定图
通过观察图7可以看出,在给定电机一个转速时,常规PID控制的速度输出在8 s左右才逐渐达到给定的转速,而RBF在线整定PID控制的速度输出在2.5 s左右就达到了给定的转速。由此说明,RBF在线整定PID控制相比常规PID控制更高效。PID控制的三个参数kp、ki、kd在RBF网络的在线整定下的变化情况如图8所示。
在仿真试验的第10 s给电机加上30 Nm的负载,持续1 s。加负载控制如图9所示。加负载PID参数整定如图10所示。
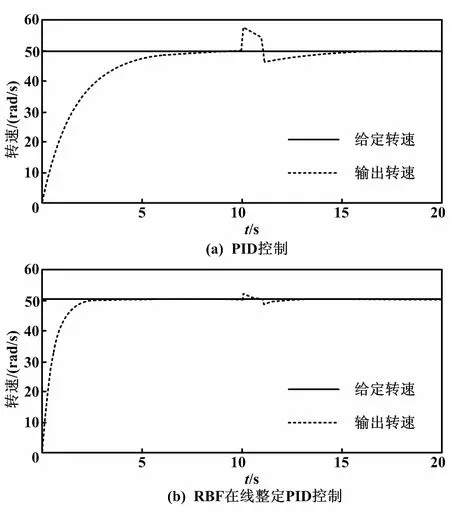
图9 加负载控制图
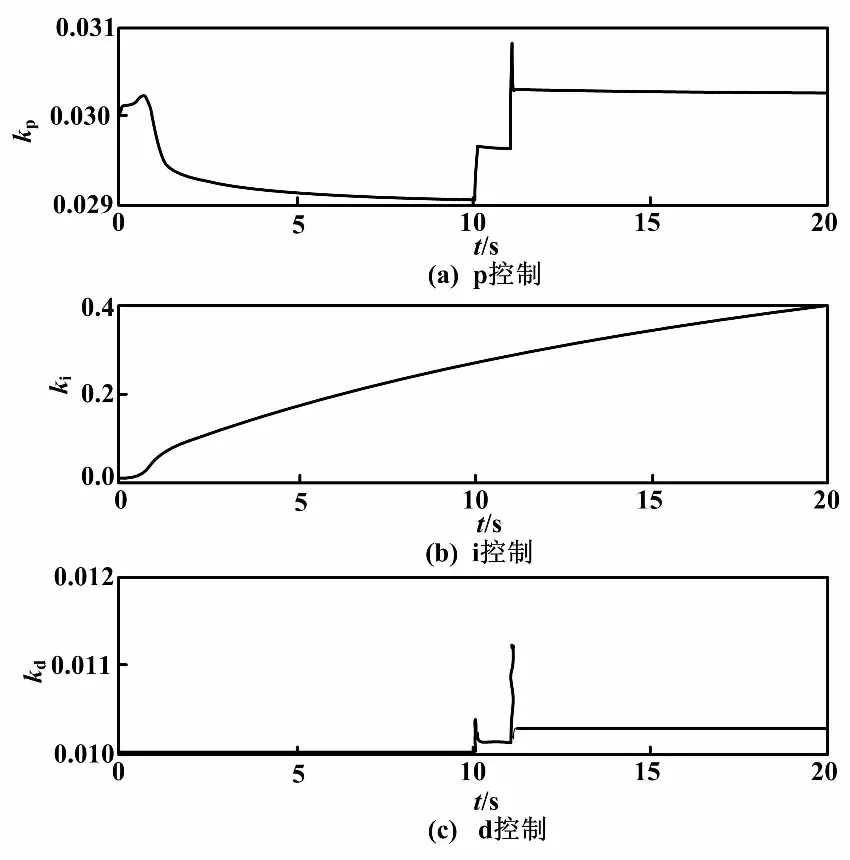
图10 加负载PID参数整定图
从图9可以看到,常规PID控制在突然给电机加上负载的那一刻,电机的速度输出发生了比较明显的变化,一直到第13 s左右才逐渐恢复稳定。而在RBF在线整定PID控制的情况下,电机的速度输出几乎没受到什么影响。从图10可以看出,在加上负载的那一刻,PID控制参数在RBF的整定作用下发生了突变,以实现对电机的自适应控制。因此可以说明,相比常规PID控制,RBF在线整定PID控制,能更好地减小电机在工作过程中遇到的负载变化所带来的影响。
6 结束语
本文针对电动汽车中永磁同步电机,建立了速度电流双闭环矢量控制的数学模型,并在Matlab平台上用m语言编写了RBF神经网络在线自整定PID控制参数的程序。通过反复测试并修改网络的神经元个数和学习率等参数,得到了一个较为高效的控制系统。仿真试验结果表明,在具有多变量和非线性特性的永磁同步电机系统的速度控制中,RBF在线自整定PID控制相比常规PID控制具有较好的控制效果,能够很好地实现电机速度控制的实时性、抗干扰能力和自适应能力。
