高中生物理科学论证能力表现——基于Rasch模型的测试评价

郑 颖 张军朋 张玉发

(1. 华南师范大学物理与电信工程学院,广东 广州 510006； 2. 广东省新兴县惠能中学，广东 云浮 527400)

21世纪以来的科学教育研究特别重视科学论证,认为科学论证是诠释科学思维的关键要素,指向科学学习的科学论证可以帮助学生发展科学探究能力、建构科学知识并促进科学概念转变和理解、提升科学认识论水平、提升推理能力、批判思维能力和交流能力[1].在这样的大背景下,我国新修订的《普通高中物理课程标准》将科学论证纳入了学科体系,使之成为物理学科核心素养中科学思维的一个重要构成要素;标准认为科学论证是物理课程中的重要内容和学习方式,也是物理教学中的重要教学目标,要求学生具备科学论证的意识和能力[2].因而,基于物理学科背景,对学生科学论证能力发展状态的精准评价与诊断就显得尤为重要.本研究基于Rasch模型开发测试工具、检验测试工具的质量,尝试利用工具测量样本学生的“物理科学论证能力”,并分析其发展特征.

1 物理科学论证能力的内涵及其水平构建

本研究在概述能力与科学论证的内涵和研究基础上,提出了物理科学论证能力的定义,即物理科学论证能力是指学生能基于对物理问题情境的描述和分析,依据现有证据,进行合理推理,支持正确观点或反驳相异观点所必须的、稳定的心理特征.其中,观点是指基于对物理问题情境的描述与分析而做出的判断;证据是指支持观点的物理知识,包括物理模型与规律等;推理过程是指联系观点和证据的因果关系链,包括演绎推理和归纳推理等;反驳是指运用物理知识对相异观点以及支持该观点的证据或推理过程的质疑和批判,其过程本身也是在论证[3].

对于学生物理科学论证能力的表现评价则是借鉴了SOLO分类理论的思想[4],从学习行为变化结果上考查学生的物理科学论证能力,即从观点、证据、推理过程、反驳4个方面将学生的行为结果分为5个不同的水平来评价学生的表现,并将其作为后续测试工具编制、评分标准制定、数据分析与讨论的理论框架和重要依据.划分的水平如表1所示.

表1 物理科学论证能力水平划分[3]

需要说明的是,由于本研究主要是基于物理问题情境对学生的物理科学论证能力进行测评,且测评的知识载体并不涉及物理课程之外的知识,故试题的编制没有涉及水平5这一层级的考查,对学生的作答情况只根据前4个水平进行处理.

2 物理科学论证能力表现测试工具的开发

物理科学论证能力作为一种内隐的心理特质,需要通过外显的行为来进行诊断和评估,即可以基于对学生解决物理问题时的外在表现的描述和分析,进而对学生的科学论证能力水平作出合理推断.本研究采用书面测试题的方式来开发测试工具,进行物理科学论证能力表现评价.

2.1 测试工具的开发过程

测试工具开发的科学有效性就直接关系到测试结果的可靠性,因此,必须以严格的命题程序来保证测试题的质量以及评价的效度.本研究的测试工具开发过程主要包括以下环节:综合核心知识和物理科学论证能力表现规划命题双向细目表;基于双向细目表选择情境素材以命制试题,试题类型采用开放性试题;基于物理科学论证能力水平制订评分标准,采用等级评分;邀请物理教学专家和参加省培的物理骨干教师对编制的试题提出修改意见,同时请部分学生试做并提出相应意见,根据专家和师生意见对试题进行初步修改;编码试题并组卷,然后进行试测;运用Winsteps软件对测试结果进行分析,即基于Rasch模型对测试工具的信度、试题与模型匹配度(MNSQ)等相关质量指标进行考察,对不符合要求的试题进行修订,然后再次进行试测,直到整个测试工具满足Rasch模型的参数要求.

2.2 测试工具的质量评估

为了检验并优化测试工具的质量,本研究共进行了两轮试测,测试时间均为40分钟.第一轮试测的被试学生为南宁市某高中高二两个班级共110人,回收的有效测试卷为106份,有效率为96.3%.用Winsteps软件对第一轮试测结果进行分析,结果表明,测试工具的总体信度为0.96,非常理想.而对应于每道试题的信度,在Rasch模型中表现为各试题的MNSQ值;当MNSQ的值在0.7到1.3之间时,说明试题信度符合要求[5].本轮测试中有部分试题的MNSQ值不符合MNSQ的取值范围,因此对这部分试题进行改编与修订,再进行第二轮试测.第二轮试测的被试学生为梧州市某高中高二两个班级共112人,回收的有效测试卷为107份,有效率为95.5%.同样运用Winsteps软件对测试结果进行Rasch分析,结果表明,测试工具的总体信度为0.92,较为理想.试题MNSQ值最大值为1.20,最小值为0.77,即所有试题的MNSQ值在0.7到1.3之间,表明试题与模型的匹配度较好,测试工具可用于实测来评价学生的物理科学论证能力.

3 物理科学论证能力表现的测评分析

实测选取了云浮市某高中高二的5个班级,其中2个为实验班,3个为普通班,共发放测试卷250份,回收的有效份数为208份,有效率为83.2%.其中男生128人,女生80人.首先,进一步检验了测试工具的质量.运用Winsteps软件对样本学生实测所获数据进行Rasch分析,结果表明,测试工具的总体信度为0.97,且所有试题的MNSQ值均落在0.7到1.3之间,满足信度要求,这说明测试所获数据能用于后续的表现评价分析.

3.1 样本学生物理科学论证能力总体表现水平

运用Rasch模型对全部测试数据进行处理可得到个体能力值(即logit得分),也可得到样本学生总体物理科学论证能力表现的怀特图(Item-map).表2是样本学生总体物理科学论证能力的描述性统计数据.由表可知,样本学生的物理科学论证能力的logit得分全距为4.65,标准差为0.71,样本学生能力水平分布广,差异显著;而能力均值为-0.14,均值的标准误为0.05,说明数据具有较高的可信度.

表2 样本学生总体物理科学论证能力的描述性统计

基于样本总体的怀特图来划分样本学生的物理科学论证能力水平,划定的水平分界值具体如下:当学生的能力值小于-1.20时,可认为学生的物理科学论证能力水平位于水平1;当学生的能力值在[-1.20,-0.24)时,则位于水平2;当学生的能力值在[-0.24,0.77)时,则位于水平3;当学生的能力值大于等于0.77时,则位于水平4.总体学生在各水平上的人次百分比如图1所示.

图1 样本学生物理科学论证能力水平分布

由图1可知,全体样本中有3.85%的学生处于水平1;有35.58%的学生处于水平2;有48.56%的学生处于水平3;有12.02%的学生处于水平4.总体来看,样本学生的物理科学论证能力主要集中在水平2和水平3,总人数占到84.14%.

3.2 不同班级学生物理科学论证能力表现的比较分析

将两个实验班分别编号为1班和2班,3个普通班分别编号为3班、4班和5班,然后对5个班级的学生的能力值做统计平均,得到学生的能力均值结果如表3所示.

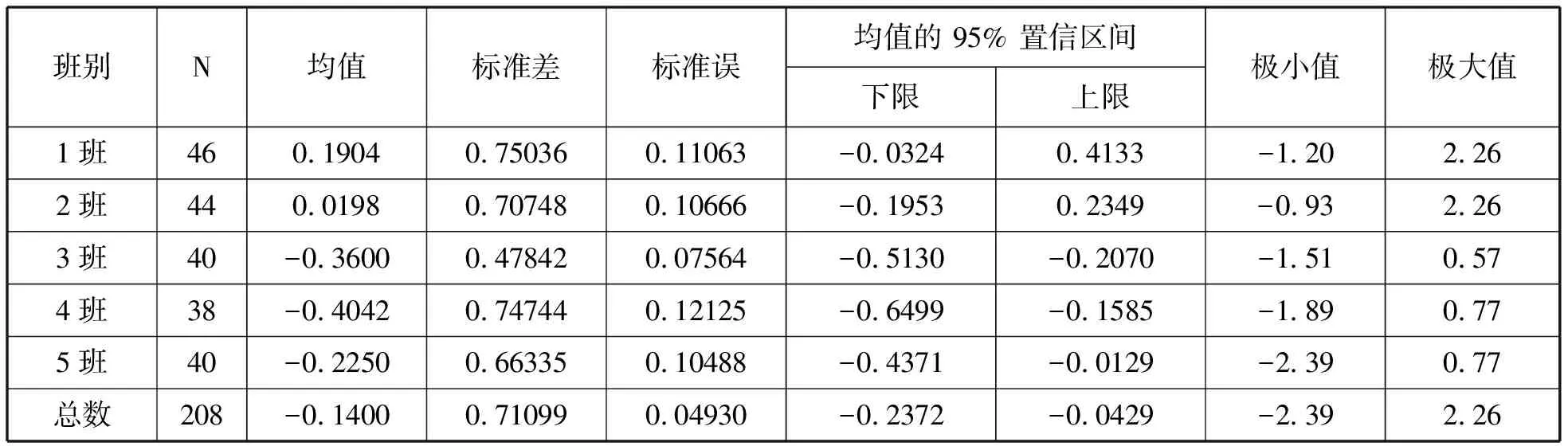
表3 不同班级学生物理科学论证能力的描述性统计

由表3可以看出,在实测中,1班学生的能力均值为0.1904,整体水平处于水平3;2班学生的能力均值为0.0198,整体水平处于水平3;3班学生的能力均值为-0.3600,整体水平处于水平2;4班学生的能力均值为-0.4042,整体水平处于水平2;5班学生的能力均值为-0.1400,整体水平处于水平3.总体而言,实验班的能力表现比普通班好.另外,各班级学生的能力均值估计标准误均小于0.20,保证了样本学生具有较好的代表性.图2则更直观地显示了各个班级学生的能力均值.

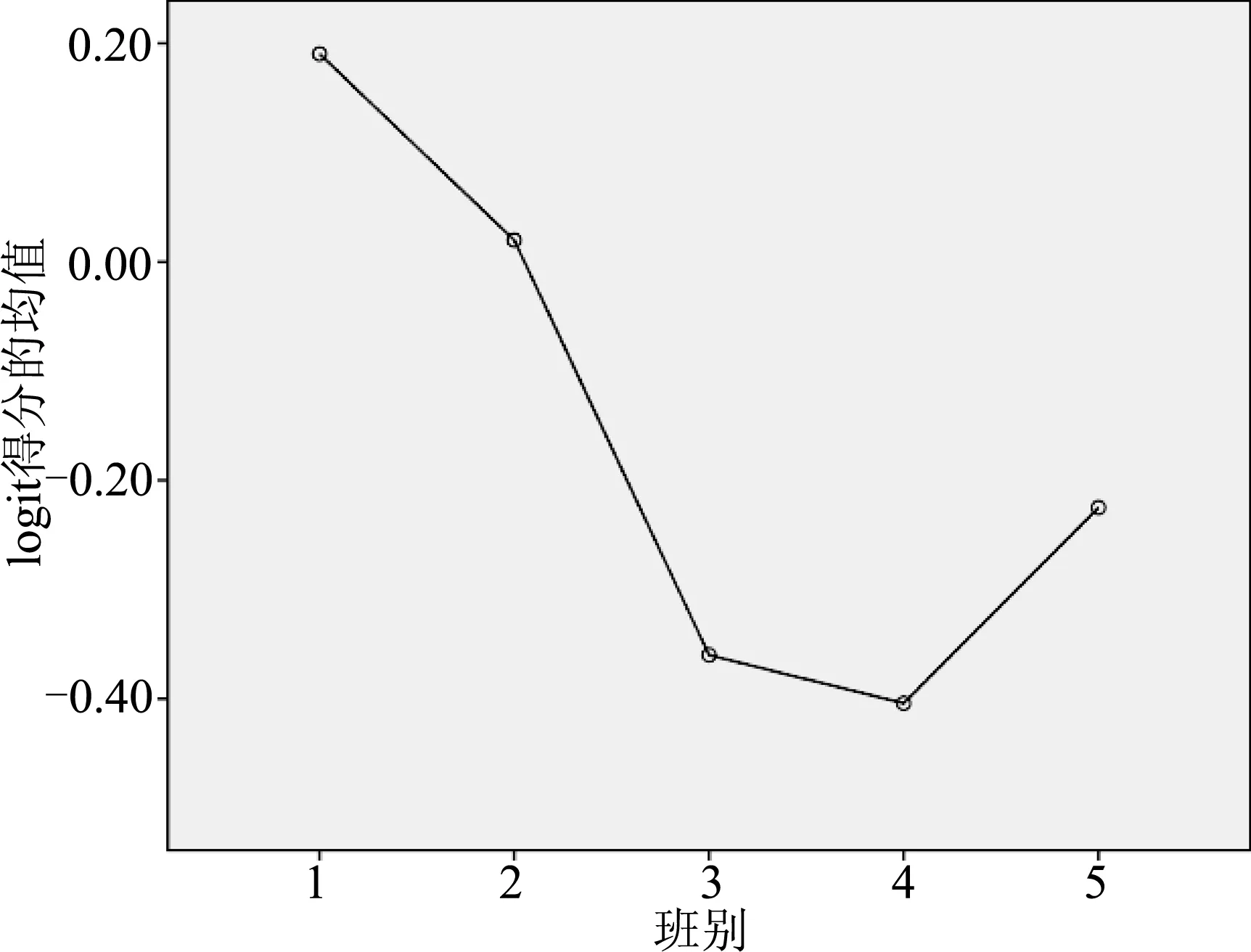
图2 不同班级学生物理科学论证能力均值图

虽然不同班级学生的能力均值有差异,但这种差异是否具有统计学意义,还需要对不同班级的学生能力值进行单因素方差分析(One-Way ANOVA),检验其差异性,结果如表4所示.

表4 不同班级学生物理科学论证能力方差分析

方差齐性检验结果显示,对于学生的能力值,Levene统计量的值为1.752,对应显著性值为0.140,大于显著性水平0.05,说明方差齐性.而方差分析结果显示,F值对应的显著性值为0.000,小于显著性水平0.05,说明五个班中至少有一个班和其他四个班存在显著性差异.因为各班级学生logit得分方差齐性,所以选用LSD方式对数据进行检验,结果如表5所示.

表5 不同班级学生物理科学论证能力均值多重比较统计

续表

*. 均值差的显著性水平为 0.05.

从多重比较结果可以看出,在能力均值上,除了2班和5班无显著性差异外,实验班与普通班之间均有显著性差异,且实验班之间和普通班之间均无显著性差异.

3.3 样本学生物理科学论证能力表现与物理成绩的相关性分析

将样本学生的能力值(即logit得分)和物理成绩进行相关性分析.物理成绩数据是学生高二下学期期中考试的物理成绩,该阶段学生已学完本研究开发的测试工具包含的所有知识载体,故将其代表学生平时的物理成绩进行分析.图3是样本学生的logit得分与物理成绩的散点分布图.

从图3中可以初步判定样本学生的物理科学论证能力与物理成绩之间呈线性相关,可以进行二元变量相关分析.表6为皮尔逊相关的统计分析结果.从表中可以看出,相关性检验得出的皮尔逊相关系数为0.551,显著性(双侧)值为0.000,小于显著性水平0.01,说明样本学生的物理科学论证能力与物理成绩存在着显著的正相关.

图3 样本学生logit得分与物理成绩的散点分布图

logit得分物理成绩 logit得分Pearson相关性10.551∗∗显著性(双侧)0.000N208208物理成绩Pearson相关性0.551∗∗1显著性(双侧)0.000N208208∗∗. 在0.01 水平(双侧)上显著相关.

3.4 不同性别学生物理科学论证能力表现的比较分析

表7是实测中不同性别学生物理科学论证能力的描述性统计数据.表8是实测中样本学生物理科学论证能力性别差异的独立样本t检验结果.

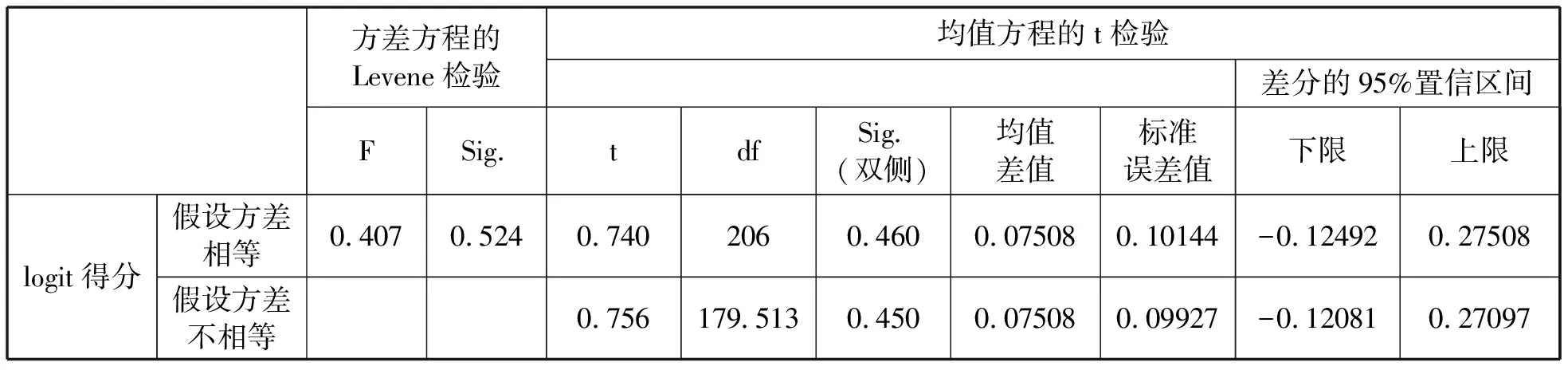
表8 样本学生物理科学论证能力性别差异的独立样本T检验

由统计结果可以看出,男生物理科学论证能力的能力均值为-0.1112,女生的能力均值为-0.1862,男生的能力均值比女生高0.075,说明男生的表现平均略好于女生.另外,方差齐性检验结果显示,对于学生的能力值,Levene统计量的F值等于0.407,显著性概率(Sig.)为0.524,大于显著性水平0.05,说明方差齐性.而均值方程的t检验结果显示,双侧显著性概率(Sig.)为0.460,大于显著性水平0.05,说明男生和女生的物理科学论证能力的均值无显著性差异.

4 测评结果讨论与教学建议

本研究对“物理科学论证能力”进行了水平建构、测试工具的开发及优化、能力测验及数据分析.研究表明,修订后的测试工具符合Rasch模型的相关质量指标,具有可信性.而实测结果表明,题目情境或知识内容的难易程度不同,对学生物理科学论证能力的鉴别结果也有所不同.总体来看,样本学生的物理科学论证能力与物理成绩存在着显著的正相关,其能力水平主要集中在水平2和水平3,只有12.02%的学生处于较高水平.虽然男生的表现平均略好于女生,但两者并无显著性差异.5个班级学生的能力均值由大到小为1班>2班>5班>3班>4班,除了2班和5班无显著性差异外,实验班与普通班之间均有显著差异,且实验班之间和普通班之间均无显著性差异.样本学生的具体表现有以下特征:一是学生倾向于调用生活经验或已有的认识,并非基于事实证据进行科学地论证;二是学生没有深刻理解物理概念和规律的内涵和外延,往往罗列相关的概念规律,但不能和问题情境相结合进行相关论证;三是学生在进行科学论证时,容易根据部分的事实证据进行推理,缺乏清晰连贯阐述推理过程的意识,在应用所学知识说明所得结论时不能清晰表达,逻辑推理不够严密.

样本学生在此次测试中的物理科学论证能力表现从一定程度上可以对课堂教学形成诊断作用,在测试结果基础上,提出基于科学论证能力培养为主的教学建议如下.

(1) 在物理教学中显化科学论证,培养学生科学论证的意识.

在教师为学生创造科学论证机会之前,第一步工作是要在课堂教学中显化科学论证,让学生知道科学论证包含观点、与观点相关的证据、联系观点和证据的推理以及反驳这些基本构成要素,并且要把这些融入教学语言,向学生展示科学论证的过程和方法,学生才可以通过模仿教师的示范过程,知道论证的形式、推理的过程以及证据的使用等,从而发展学生对科学论证的认识,增强学生进行科学论证的意识.

(2) 创设科学论证的学习情境,让学生经历科学论证的过程.

在物理教学实践中,创设让学生参与科学论证活动的学习情境,引导学生发现问题,通过科学论证解决问题,经历概念、规律的学习理解过程,可以促进学生科学论证能力的发展.那如何在课堂上创造良好的科学论证环境呢?本研究认为,教师可以在课堂教学中提出一些开放性问题来引发学生思考,让学生陈述自己的观点,并基于学生的回答进行追问,如“你为什么这么认为”、“你是怎么得到这个结论的”.在这种互动过程中,引导学生说出其中的原因和理由,同时引导学生之间对彼此的观点和推理过程进行相互评论,指出各自推理过程中可能存在的自相矛盾的地方,激发学生使用更多的证据来支持自己的观点.当学生遇到困难时,教师可以通过搭建“支架”引导学生进行推理,帮助学生探索原始认识中的不正确之处,让学生重新建构正确的推理过程,同时引导学生反思自己观点的转变过程和转变原因,充分认识原始论证过程和科学论证过程之间的差异,帮助学生迈上台阶,使学生在物理现象的宏观描述与微观解释的沟通中、在从定性描述到定量描述中、在物理过程的静态与动态分析中逐步发展科学论证能力.