基于碰撞性能的车身刚度链设计方法*

郭 毅，刘子建，秦 欢

（湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082）

前言

在车身概念设计阶段采用拓扑优化的方法，并考虑车身弯扭刚度和模态等性能要求，以实现设计域内材料的最优分布是车身正向设计的一种常用做法。如QUINN［1］以车身刚度性能为主导，综合考虑多种静载工况，确定白车身合理的材料分布。常伟波等［2］采用拓扑优化的方法得到车身的初步结构和尺寸，再结合正面碰撞安全性要求优化了矩形薄壁前纵梁的截面尺寸。YIS I等［3］采用等效静态载荷法（ESL），在考虑应变能和人体损伤因素的同时，使用线性算法对车身碰撞优化问题进行了研究。高云凯等［4］对现有模型进行了静力、模态和100%RB碰撞分析，优化了车身结构尺寸。QIN H［5］开发了面向对象的MATLAB工具箱，用于快速优化车身主断面参数。刘子建等［6-7］提出了基于刚度链的车身正向概念设计方法，用于优化车身设计。上述有代表性的研究成果在促进车身正向设计技术发展的同时，也展示了在综合考虑车身动静态刚度性能和碰撞安全要求的前提下，获取更加实用高效的车身正向优化设计方法的必要性。

基于上述讨论，在探讨车身正向概念设计流程的基础上，建立完善了车身刚度链数学模型，分析了车身动态刚度、静态刚度、正面碰撞安全等性能要求与车身整体轻量化设计的关系，建立了考虑上述综合因素的车身结构概念设计优化模型，以车身轻量化为目标，采用遗传算法优化车身各主断面的参数，并通过对应的有限元模型仿真验证了所提出设计方法的有效性。

1 车身简化几何模型

在深入研究车身刚度链设计方法和车身正面碰撞安全性要求的基础上，提出了重点考察前纵梁碰撞、车身弯曲工况和扭转工况的车身正向概念设计流程，如图1所示。

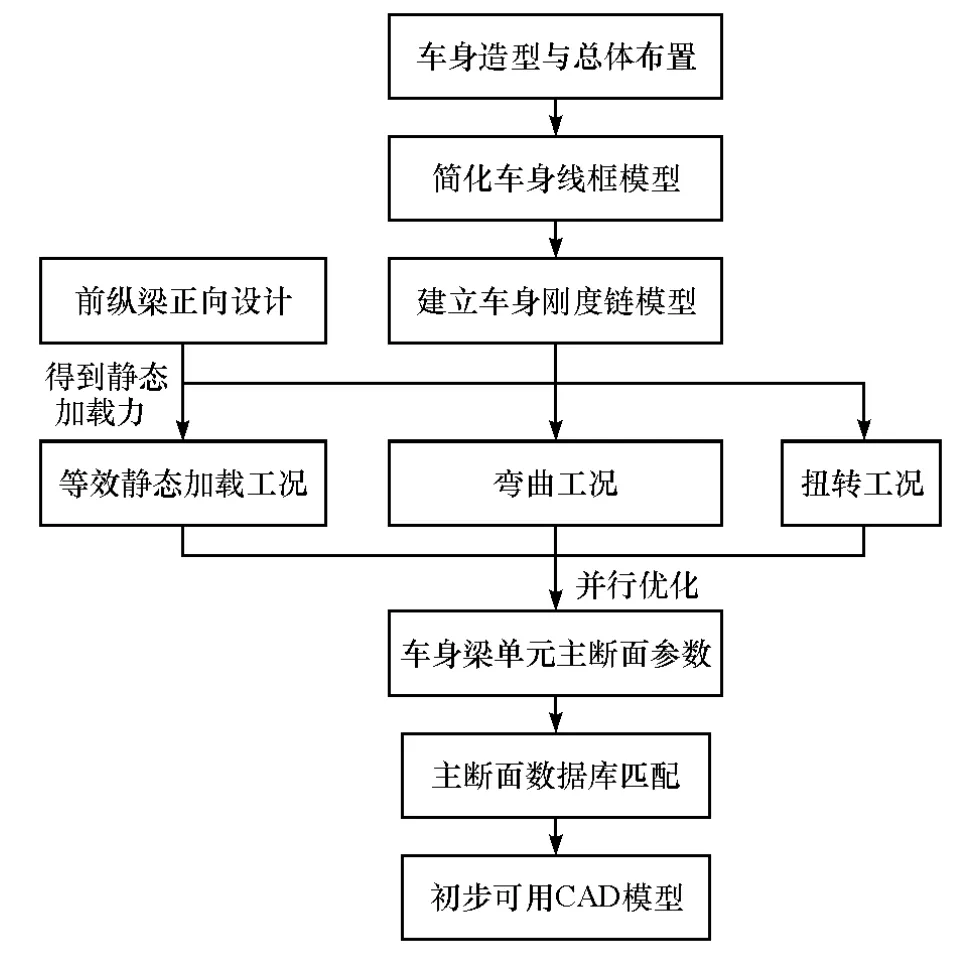
图1 车身正向概念设计

依据该设计流程，本文中以一款A级车为研究对象，根据市场需求，确定整车基本参数，如表1所示。

表1 整车设计参数

该款车型提供的原始数据是车身造型曲面。依据车身造型和市场类似主流车型的梁结构布置形式，经过简化得到如图2所示的车身简化几何模型。

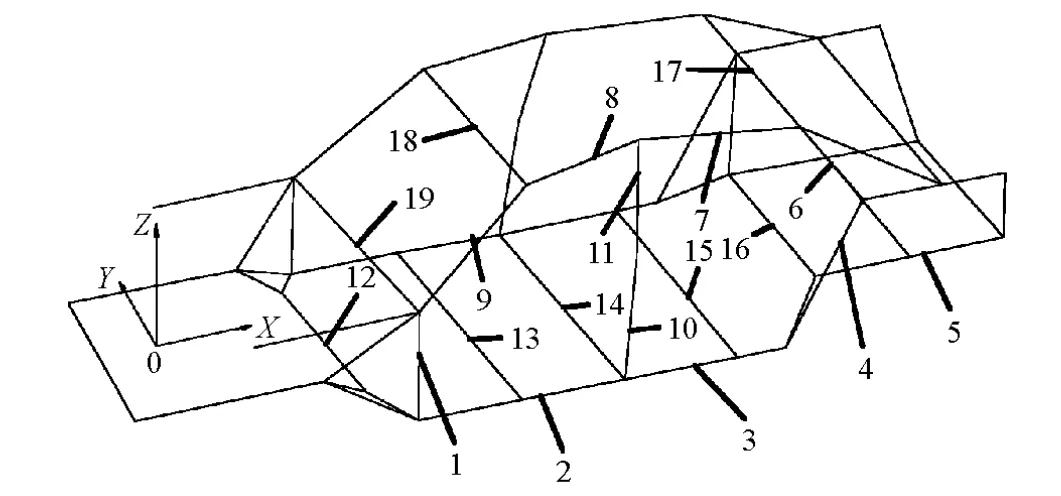
图2 车身简化线框模型

利用车身结构的对称性，确定1／2车身上19个梁单元主断面位置。主断面名称与对应梁结构编号见表2。

表2 主断面与结构件对应关系

2 车身刚度链模型的建立

依据简化几何模型描述的车身拓扑结构，采用结构力学原理建立车身刚度链力学模型，利用传递矩阵法，将车身整体结构的刚度分析问题转换为刚度链模型中若干子单元或子刚度链之间的载荷传递问题，建立完善的刚度链计算模型。

2.1 静态刚度链建模

依据简化几何模型确定的车身拓扑关系，利用车身结构的对称性，建立刚度链力学模型，如图3所示。图中1／2白车身刚度链模型包括26个梁单元，24个节点。车身左侧围由3条子刚度链组成，分别为1（0-1-2-3-4-5-6-7），2（1-8-9-10-11-12-13-6）和 3（4-14-10），整车刚度链由左侧围、右侧围各3条子刚度链及横梁10条子刚度链，共16条子刚度链组成。

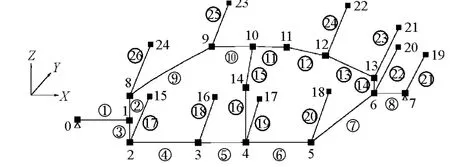
图3 车身刚度链力学模型

考虑到同一根梁单元对应多个组成单元，或梁单元截面尺寸变化较大，如门槛梁和B柱等，可将之前确定的19个主断面详细划分为26个截面属性集合。定义梁单元的截面面积A、惯性矩Iy与Iz和极惯性矩Ip为截面属性集合。

记截面属性集合为）

以子刚度链1（0-1-2-3-4-5-6-7）为例，因为结点0处受铰接约束，其轴力、扭矩和Y，Z方向弯矩及位移均为0，则节点状态向量为

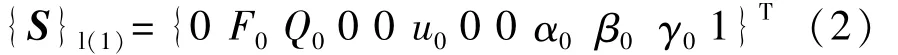
式中：F0，Q0分别为节点0处的Y，Z方向的约束反力；u0为节点0处 X方向线位移；α0，β0，γ0分别为节点0处X，Y，Z方向角位移。同理，可以确定子刚度链1上其余节点和其它子刚度链上节点的状态向量。

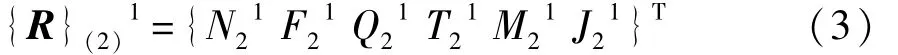
式中：｛S｝l（i），｛S｝r（i）分别为单元 i左端和右端节点状态向量；［F］（p）为节点 p的载荷矩阵；［T］（q）为全局坐标系下单元q左端与右端节点间的传递矩阵。

进一步可以建立节点耦合方程，如图3中节点1的耦合方程为

同理，可建立整车22条子刚度链传递方程，分别为F1，F2，…，F22，建立整车节点耦合方程，分别为Q1，Q2，…，Q22，由此可建立联立方程组，该方程组包含的未知数与方程数均为480个，为线性方程组，可联立解出所有的状态向量和载荷向量。

鉴于白车身材料参数（弹性模量E，泊松比μ，剪切模量G）和单元长度l（i）为已知参数，最终可以求得弯曲工况下加载处的位移δ与扭转工况下加载点处的相对扭转角φ与主断面属性的关系式f1和

2.2 动态刚度链建模

鉴于人体内脏和脊柱对频率4～12.5Hz内的振动最为敏感，为满足车辆舒适性要求，车身的固有频率应该避开该频率范围，同时还要考虑行驶振动导致的车身共振，需要建立车身动态刚度链模型，优化白车身的1阶振动频率。建立动态刚度链数学模型需推导包含梁单元质量参数的刚度链节点传递矩阵。

图 4中｛S｝l（i）和｛S｝r（i）分别表示梁单元 i左端和右端节点状态向量。

式中：F为沿坐标轴的力；M为绕坐标轴的力矩；X，Y，Z为线位移；Θ为绕坐标轴的角位移。车身动态刚度链的固有频率ω与各主断面属性｛C｝的关系式可记为f3［8］，即

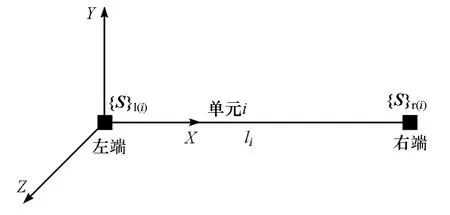
图4 梁单元模态坐标系

3 前纵梁正向设计

前纵梁是车身正面碰撞时吸收能量的主要部件，其设计的好坏是决定汽车碰撞安全性的主要因素。汽车正面碰撞过程中，薄壁直梁构件的变形吸能特性与汽车真实前纵梁的吸能特性非常接近［9］。典型前纵梁断面形状多为带焊点的帽形结构，或为带加强板的帽形结构，如图5（a）所示。因此，在概念设计阶段，可以使用如图5（b）所示截面为矩形的薄壁直梁代替真实前纵梁分析其变形吸能特性。

图5 典型前纵梁截面

3.1 前纵梁主断面参数确定

汽车发生正面碰撞时，动能的主要部分由于前舱变形而转化为内能，吸收能量的变形部件主要有前纵梁、保险杠、吸能盒、发动机罩、前指梁、副车架以及发动机综合体等。鉴于高速正面碰撞时，前纵梁吸收了碰撞总能量的50%～70%［10］，本文中针对v=48.3km／h碰撞时速进行设计，并假设前纵梁吸收了50%的碰撞能量。

单根前纵梁可吸收动能

式中M为整车质量。

根据研究报道，同级别的轿车以时速v与刚性墙正面碰撞时，前纵梁的压溃变形量约为400mm［11］，以该值为设计目标值，则

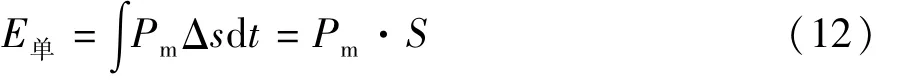
式中：Pm为平均碰撞力；S为前纵梁变形压溃距离。计算可得Pm=67.5kN。

文献［12］中提出了优化后的薄壁矩形梁平均碰撞力为

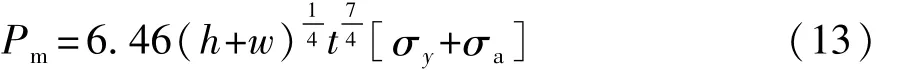
式中：h和w为矩形截面的长和宽；t为厚度；σy为材料的屈服应力；σa为能量平均应力。为了保障前纵梁在碰撞过程中不至于变形过大，同时提高其单位变形吸收的能量，前纵梁一般使用高强度钢板，本文中采用 H340LAD＋ZZF高强钢材料，σy=371.00MPa，σa=482.82MPa。

薄壁矩形直梁在碰撞中的变形模式可以分为3种，即渐进叠缩变形、Euler变形和混合变形。最理想的变形是渐进叠缩变形，在这种变形模式下，前纵梁可以吸收更多的能量，同时乘员舱的变形较小。依据文献［10］～文献［12］中对薄壁矩形梁碰撞过程的研究，可以得到截面长宽比和厚度对于变形的影响。厚度t主要影响前纵梁的吸能特性，该值越大，吸收的能量越多，但是峰值碰撞力也越大。长宽比影响直梁的变形方式，该值小于1.67时，直梁容易发生渐进叠缩变形。综合考虑上述因素，本文中选择 t=2mm，h／w=1.6，代入式（13）计算得 h=107mm，w=67mm。矩形前纵梁的参数如表3所示。

表3 矩形前纵梁参数 mm

3.2 前纵梁建模仿真

以3.1节中计算得到的前纵梁参数为基础，使用HyperMesh建立前纵梁仿真模型。在直梁后方添加300kg的质量块，作为前纵梁的配重。使用MAT24材料模拟高强钢，刚性墙使用MAT20材料。直梁单元采用6mm网格进行划分，以壳单元进行模拟，接触面动静摩擦因数均设置为0.2，将接触类型设置为Autometic，设置输出控制卡片，计算时长为70ms，并输出K文件［13］。建立的模型如图6所示。

图6 前纵梁有限元模型

使用LS-DYNA非线性求解器进行求解，利用HyperView查看后处理文件，前纵梁碰撞力随时间变化曲线如图7所示，压溃变形距离随时间的变化曲线如图8所示。

图7 碰撞力- 时间曲线

图8压溃位移- 时间曲线

图7 中采用积分法计算该曲线10～50ms的平均碰撞力约为65kN，图8表明纵梁压缩终了时压溃变形距离为380.646mm，与设计目标值对比如表4所示。

由表4可见，仿真值与目标值之间误差均在合理范围内，表明在概念设计阶段采用上述方法计算薄壁矩形前纵梁是合适的。图7中瞬时碰撞力峰值为144.8kN，峰值碰撞力的大小受多个因素的影响，可以通过在纵梁前端添加诱导槽、开弱化孔等方式调整峰值碰撞力的大小，同时增加压溃变形量。

表4 前纵梁设计参数对比

4 加载工况与主断面参数优化

4.1 加载工况

车身正面碰撞时前纵梁要经历一个动态大变形过程，如何在不进行复杂动态非线性计算的前提下，将前纵梁承受的碰撞力合理地加载在车身刚度链模型上，是在车身概念设计阶段综合考虑碰撞安全性时必须首先解决的问题。车身安全性设计规范要求正面碰撞后车身变形量应控制在确保乘员舱两侧车门至少可以打开一个。据此，本文中假设车身正面碰撞时，乘员舱仅发生近似于弹性的变形，以此作为车身安全性设计目标，并采用等效静态载荷法（ESL）模拟汽车正撞加载。

ESL方法的基本思想是将一系列静态载荷施加到模型上，使模型在同一时刻产生与动态分析相同的位移变形，这便保证了进行线性分析的模型与动态分析模型的等价性，进而将难以实现的动态非线性结构优化问题转化为线性优化问题，以便使用线性优化算法进行优化［14］。文献［15］中的研究结果表明，当优化结果满足动态非线性约束条件且算法迭代收敛时，不需要进行额外的动态非线性分析来验证模型是否满足非线性的约束条件。

文献［16］中详细介绍了静态加载的方法，步骤是在已有的汽车模型上先进行整车碰撞计算，再提取前纵梁后端的平均内力作为整车静态加载载荷。由于正向概念设计的出发点不是已有的汽车模型，无法直接使用该文献的方法。上节中讨论的矩形薄壁前纵梁吸能与压溃变形的计算和仿真方法可以很好地适用于需要频繁修改、多次计算的车身概念设计阶段。进一步分析前纵梁截面力与时间的关系，将截面力输出位置取前纵梁末端未变形处，计算结果存放在secforc文件中，可得如图9所示的曲线，就可以查看前纵梁碰撞过程中截面力随时间的变化关系。

图9 截面力- 时间曲线

从图9可以看到，碰撞过程中除前期出现峰值力以外，后续变形过程平稳，积分计算10～50ms区间平均内力F内≈51kN，将该力视为汽车发生正面碰撞时前纵梁传递给车身的内力，并作为等效静态载荷加载在前纵梁与车身连接处，方向水平向后，同时约束B柱后方车身梁单元的3个方向的平动自由度，即得等效静态加载工况，如图10所示。

图10 等效静态加载工况

车身静态刚度包括两种加载工况：（1）车身弯曲加载工况如图11所示，约束前悬3个平动自由度，约束后悬X方向平动自由度，在门槛梁位置添加1 670N的力；（2）扭转加载工况如图12所示，分别约束保险杠和后悬的平动自由度，在前悬处施加2 000N的力。

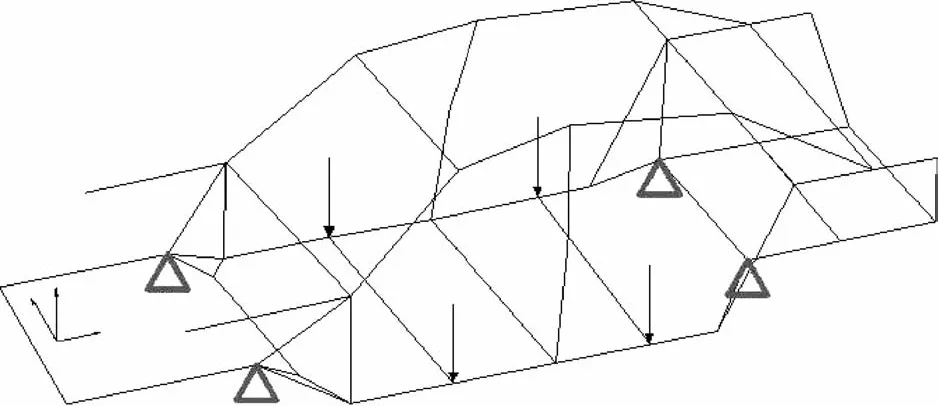
图11 弯曲工况

4.2 车身矩形主断面参数优化

车身弯扭刚度、模态以及碰撞安全性的优化，最终体现为车身主断面参数的优化，以及材料的优选和分配上。考虑到概念设计阶段主要研究车身主断面的力学性能，将复杂车身主断面简化成矩形，其截面如图13所示。

图12 扭转工况

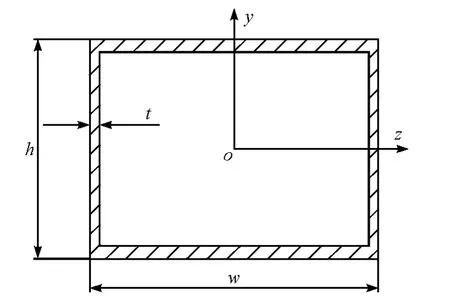
图13 主断面简化形状

考虑26个主断面属性集，定义为

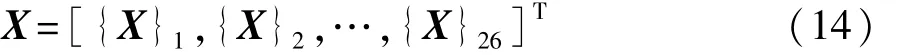
式中ρ为材料密度。依据碰撞安全性对车身刚度的要求，部分梁单元材料使用高强钢，如A柱、B柱、门槛梁和前地板横梁等，其厚度优化区间为［1.0，2.0］，其余梁厚度优化区间为［0.8，1.2］。

对弯曲工况，要求加载点处的竖直位移 δ＜1mm。对扭转工况，要求相对扭转角φ≤0.2°，其中φ=arctan（2·Δ／b），b为前悬加载点间的横向距离，Δ为扭转工况下加载点竖直位移，同时要求车身1阶固有频率大于17Hz。

结合汽车正撞法规，对车身等效静态加载变形工况要求如下：

（1）A柱变形角 ηA≤4°；

（2）底板与顶棚之间减小距离LB≤12mm。

综上所述，车身设计变量、目标函数以及约束条件可以表示为

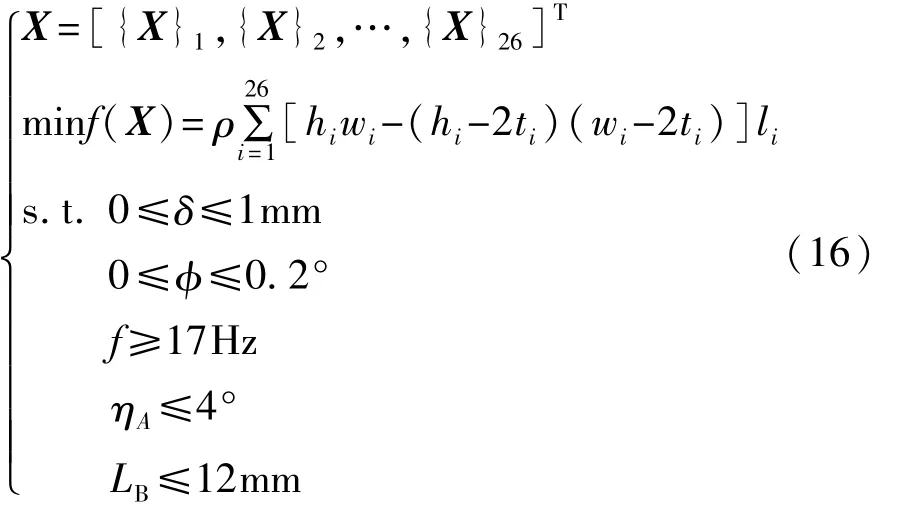
参考文献［5］，使用MATLAB编写车身静态和动态刚度链计算程序，使用遗传算法求解式（16），目标函数经过60次迭代逐渐收敛，过程如图14所示。

图14 迭代收敛过程

优化后的主断面参数如表5所示。

使用遗传算法优化后得到车身的弯曲、扭转和等效静态加载工况下的位移以及1阶模态振型，如图15～图18所示。

从优化结果来看，在满足动态和静态刚度、固有频率以及正面碰撞等效静态载荷变形约束条件下，车身最轻质量为218.46kg，弯曲工况下加载点的位移δ=0.831mm，扭转工况下加载点位移 Δ=1.806mm，相对扭转角 φ=0.138°，1阶固有频率为26.8Hz，A柱变形角 ηA=2.67°，顶棚与地板之间减小距离LB=1.45mm，满足碰撞法规对车身碰撞变形的要求。由整车的弯曲刚度和扭转刚度计算公式可得

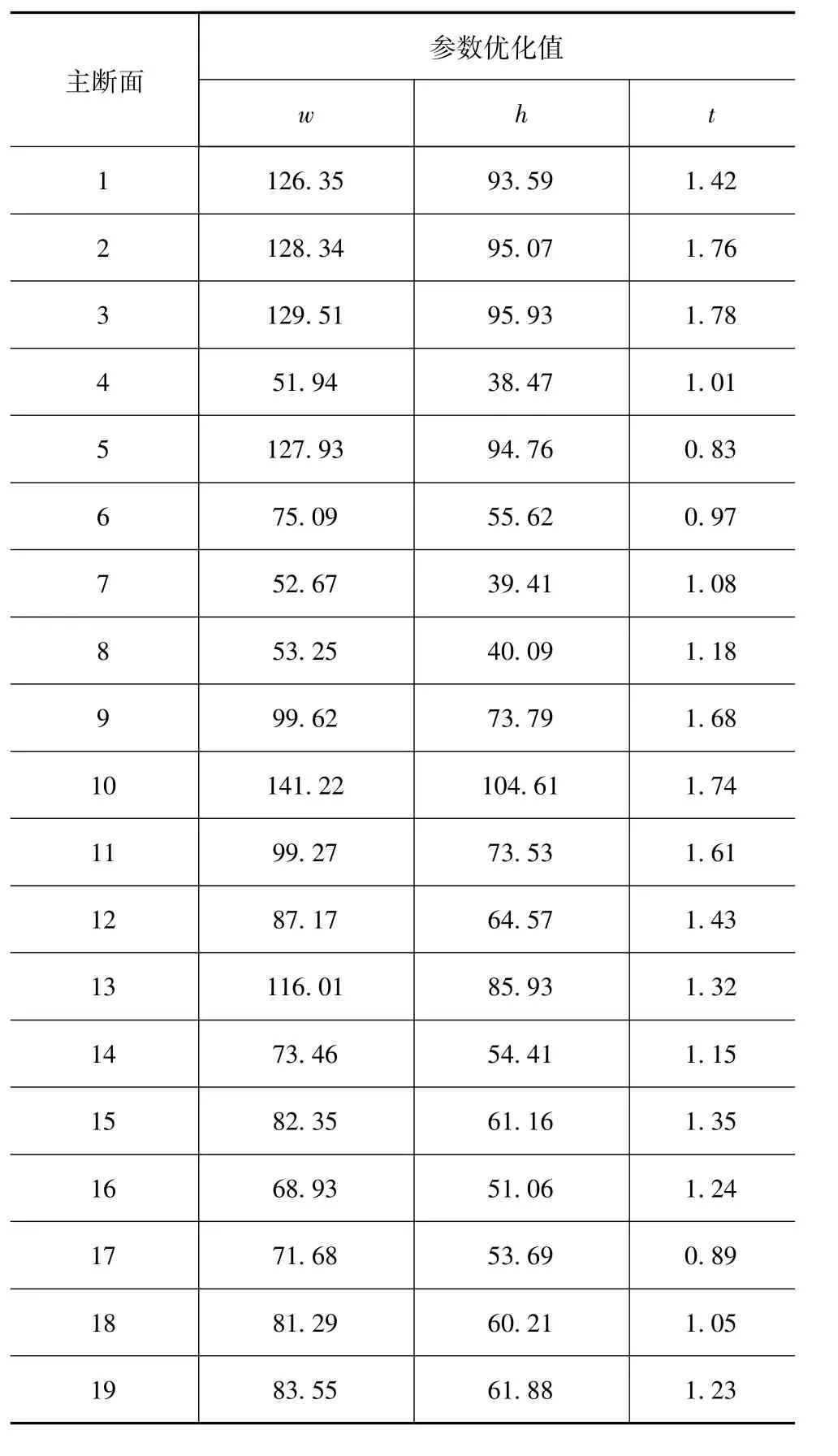
表5 26个主断面参数 mm

图15 弯曲工况

4.3 优化结果验证

为验证该刚度链设计方法的可行性，选取一款近似标杆车进行有限元仿真计算，如图19所示。

图16 扭转工况

图17 等效静态加载工况

图18 自由模态1阶振型

图19 标杆车有限元模型

对有限元模型进行静力和模态分析，得到其弯曲、扭转和1阶模态下的变形如图20～图22所示。

标杆车模型弯曲工况下加载点变形 δ′=1.774mm，扭转工况下加载点变形Δ′=1.676mm，相对扭转角φ′=0.128°；1阶模态固有频率为25.2Hz；车身质量为235.06kg。则弯曲刚度k弯′=3865.5N／mm，扭转刚度 k扭′=23437.5N·m·（°）-1。

将刚度链求解结果与有限元分析结果进行对比，如表6所示。

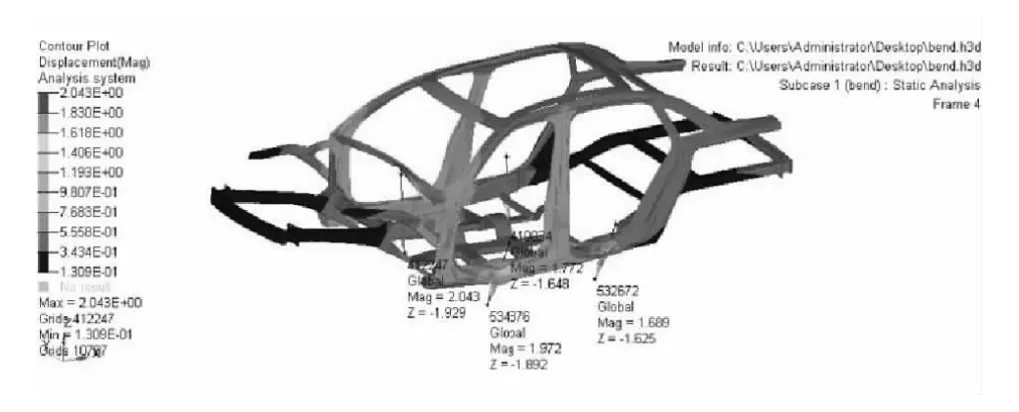
图20 弯曲工况

图21 扭转工况

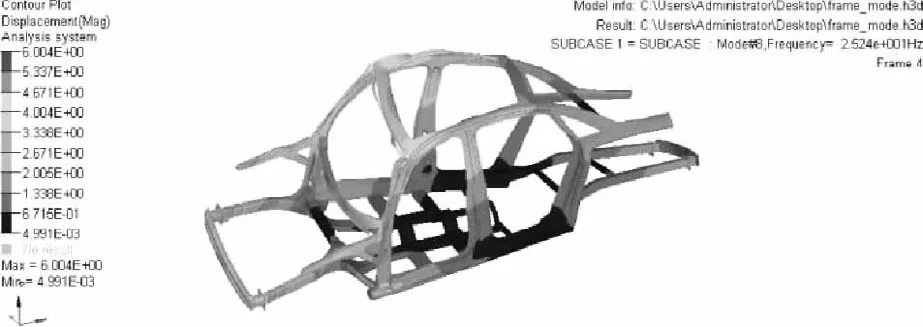
图22 1阶模态分析

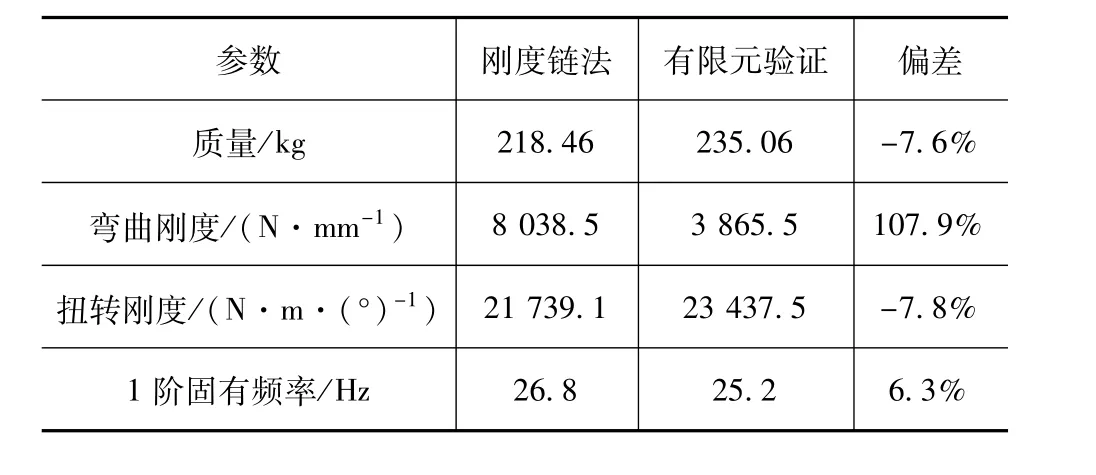
表6 分析结果对比

由表6可见，有限元计算的弯曲刚度只有刚度链法计算结果的一半左右，这是因为采用刚度链法时没有考虑车身接头柔度，计算结果的偏差与文献［17］中研究的不考虑接头柔度计算的偏差结果相一致。而质量、扭转刚度和1阶模态偏差值较小，表明采用该方法进行车身概念设计是可行的。

5 结论

在综合考虑车身静态、动态刚度和正面碰撞安全性的基础上完善了车身刚度链方法，拓展了该方法用于车身性能参数优化求解的参数类型和范围，可以在综合考虑碰撞安全性要求和刚度性能的前提下实现车身结构的快速分析和优化设计，为性能主导的车身正向概念设计提供了一种新工具。讨论车身正向概念设计流程，依据概念设计外形得到了简化的车身线框模型，确定了19个梁单元主断面位置，利用传递矩阵法建立了车身静态和动态刚度链数学模型，对正撞安全性影响最大的前纵梁进行了单独设计，得到了合理的前纵梁主断面参数。进一步以车身质量最轻为目标函数，以静态刚度、1阶模态和等效静态加载变形为约束条件，采用遗传算法优化了车身各主断面属性参数，并与近似标杆车有限元模型进行对比，验证了所提出的设计方法的可行性。

本文中只考虑了正撞过程中吸能最大的前纵梁的单独设计，没有考虑其它梁结构（如前指梁，保险杠等）在正面碰撞过程中的作用，如何将正面碰撞中其它梁单元对车身结构的影响纳入刚度链的主断面优化算法中，是后续需要研究解决的问题。