基于空间频率与时间序列信息的多类运动想象脑电分类

周杰，杨国雨，徐涛

杭州电子科技大学智能控制与机器人研究所，浙江杭州310018

前言

对于因严重运动障碍而丧失正常交流能力的患者来说，急需重新建立起一种新的与外界进行交流的方法，脑机接口（Brain Computer Interface,BCI）正是这样的一种方法。它通过信号处理、模式识别以及其他过程将与患者意图相关的脑电信号（Electroencephalograph,EEG）转换为控制信号，从而控制机器人手臂或轮椅等机器［1］。

由于EEG具有较高的时间分辨率，相对较低的成本，并且更方便患者使用的特点，BCI系统广泛采用EEG技术检测大脑活动［2］。其中基于运动想象脑电的BCI对中风患者有重要意义，它可以帮助恢复受损神经，在康复训练中发挥重要的作用［3］。在运动想象任务中，要求受试者通过想象诸如手或脚移动的特定动作来生成EEG信号［4］。然后，采用机器学习算法对EEG信号进行分类以将其转换为命令。由于数十亿个神经元之间的复杂互连，记录的EEG信号本质上是非线性、非平稳的。因此，如何从复杂的运动想象脑电中提取可以有效识别运动任务的特征是非常重要的。目前，共同空间模式（Common Spatial Pattern,CSP）方法是提取运动想象脑电相关特征最常用和最有效的方法之一，并已广泛用于运动想象BCI系统［5-6］。

CSP是一种针对两类运动想象EEG的处理算法，其通过构建空间滤波器使得两类方差差异最大化，在两类运动想象任务问题上得到很高的分类准确率。对于多类运动想象分类任务，已经提出一对多 CSP（One Versus Rest CSP,OVR-CSP）［7］和一对一CSP（One Versus One CSP,OVO-CSP）［8］，然而分类结果并不理想。这在一定程度上是因为当运动想象EEG未选取运动想象相关频率范围时，对CSP特征执行的分类通常会导致准确性较差［9］。因此出现了一些改进的CSP，例如子带共同空间模式［9］、滤波器带通用空间模式［10］。这些方法的思想是将CSP与频率信息结合，使原始EEG分解成多个频带，并在每个频带上使用CSP来选择最具有区别性的特征。

但是结合频域信息的CSP仍存在不足，EEG本质上是一个高度非平稳的时间序列信号，时间序列信息对于提高CSP特征提取和后续分类的性能也至关重要［11］。递归神经网络（Recurrent Neural Network,RNN）是一类人工神经网络，它通过单元之间的连接形成一个有向循环创建了网络的内部状态，从而可以有效利用输入信号的时间信息进行时间序列分析。近年来，RNN被广泛应用于时间序列的信号处理中，并已成为语音识别［12］、机器人运动识别［13］、图像文本识别［14］、自然语言处理［15］等领域的有效模型。然而，传统的RNN在训练过程中存在梯度爆炸或梯度消失的问题，导致RNN无法有效利用早期的历史信息。针对这个问题，Hochreiter等［16］将记忆单元引入到传统的RNN中以存储长时间信息，提出长短期记忆网络（Long Short-Term Memory,LSTM）。

为了有效利用EEG的空间频率与时间序列信息，获得更好的分类效果，本文结合离散小波变换（Discrete Wavelet Transform,DWT）、CSP和LSTM神经网络的特点，提出一种基于空间频率与时间序列信息的多类运动想象EEG特征提取方法，并采用BCI竞赛III中Dataset III-a的K3受试者数据进行分类验证。与传统脑电特征提取算法相比，分类准确率有较大提高。

1 方法

1.1 DWT

小波变换是一种时频分析方法，由于其多分辨率特性，适合对EEG等非平稳信号进行特征提取。多分辨率分析的步骤如图1所示。初始DWT由连续应用低通滤波器和高通滤波器组成，离散信号经DWT分解为多个小波分量。其中，h［n］表示高通滤波器，g［n］表示低通滤波器，x［n］表示同时通过高低通滤波器的EEG信号注释，↓2表示两倍下采样。重复该过程，直到每个通道的EEG信号被分解成n层小波细节，即D1,D2,…,Dn，以及近似系数An。

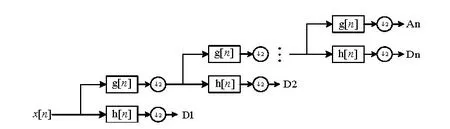
图1 离散小波多分辨率分析结构图Fig.1 Block diagram of multi-resolution analysis of discrete wavelet transform(DWT)

1.2 OVR-CSP

CSP方法的原理：首先，两类实对称矩阵（协方差矩阵）同时对角化，并应用主成分分析方法排除两种任务的共同部分，提取不同部分。进而，再通过空间因子和相应的空间过滤器将特定信号成分提取出来。为了将CSP应用到多分类问题常采用一对多方法，该方法是把其中一类模式当成一类，而余下的所有模式当成另外的一类，从而形成一个两类的CSP，这样依次对每一类信号计算对应的CSP空间滤波器。以一个带有不同类别标签的4类运动想象脑电数据为例。该算法的具体过程表示如下：

设Xi∈RN×T,i=1,2,3,4分别表示4类运动想象原始EEG，其中N表示脑电数据集的通道数，而T表示每个通道的采样点数，则可以得到EEG的归一化协方差矩阵：

其中，是矩阵Xi的转置矩阵，trace是矩阵对角线元素的总和。对每一类想象动作多次实验得到的空间协方差矩阵取平均得到平均协方差矩阵：

其中，Ci表示第i类的试验次数，表示所有第i类实验协方差矩阵之和，则4类的平均协方差之和为对进 行 特 征 值 分 解，构建白化矩阵W1：

其中，Λ代表分解后的特征值矩阵，U0是与特征值矩阵相对应的特征向量矩阵。把类别1分为一类，剩下的类别2、3、4合并为一类（计算其他类时，同理），则可将平均协方差矩阵转换为：

可以证明S1和S2具有相同的特征向量，即Σ1=Y1Λ1YΤ1,Σ2=Y1Λ2YT1,Λ1+Λ2=Ι，其中I是单位矩阵。由于两个矩阵相应特征值之和总是1，因此对于S1具有最大特征值的特征向量对于S2具有最小特征值，反之亦然。因此该算法按照特征值的大小，将矩阵U1中的特征向量依次由大到小排列，然后分别选择对应于Λ1和Λ2中m个最大特征值的2m个特征向量，形成一个新的矩阵U′1，它们对于区分两个类是最优的。依据矩阵U′1和白化矩阵W1构造类别1的空间滤波器：同理可得其余类别的空间滤波器W4，将每个运动想象脑电信号通过4个空间滤波器滤波后得到的4个信号组成新的信号：j∈1,…,n,其中n表示EEG总数。最后，将能量信号的方差规范化和取对数后为最终的特征：

1.3 LSTM

RNN模型的输入由两个输入组成：一个是当前时刻的输入，另一个是前一时刻隐藏层的输出。因此，RNN具有记忆功能，可以有效利用输入信号的时间信息进行时间序列分析。但在传统的RNN中，在梯度反向传播阶段期间，梯度信号可能多次（与时间步数一样多）乘以隐藏层神经元之间连接的权重矩阵。如果矩阵中的权重很小，则可能导致消失梯度，在数据中学习长期依赖关系的信息也会变得更加困难。相反，如果这个矩阵中的权重很大，则可能导致梯度爆炸。

这些问题是提出LSTM模型的主要动机，它引入了记忆单元，如图2所示。记忆单元由4个主要元件组成：具有自回归连接的神经元（与自身的连接）、输入门、忘记门和输出门。自回归连接的权重为1.0，并且确保除外部干扰的情况下，记忆单元的状态可以从一个时间步到另一个时间步保持恒定。输入门可以允许输入信号改变或保持记忆单元的状态。另一方面，输出门允许记忆单元的状态对其他神经元产生影响或阻止它。最后，忘记门可以控制记忆单元的自回复连接，允许单元根据需要记住或忘记其以前的状态［17-18］。

设Xt为t时刻的输入矢量，对于本文中使用的LSTM单元结构，正向传播的矢量公式如下：

图2 LSTM记忆单元Fig.2 Memory units of long short-term memory(LSTM)

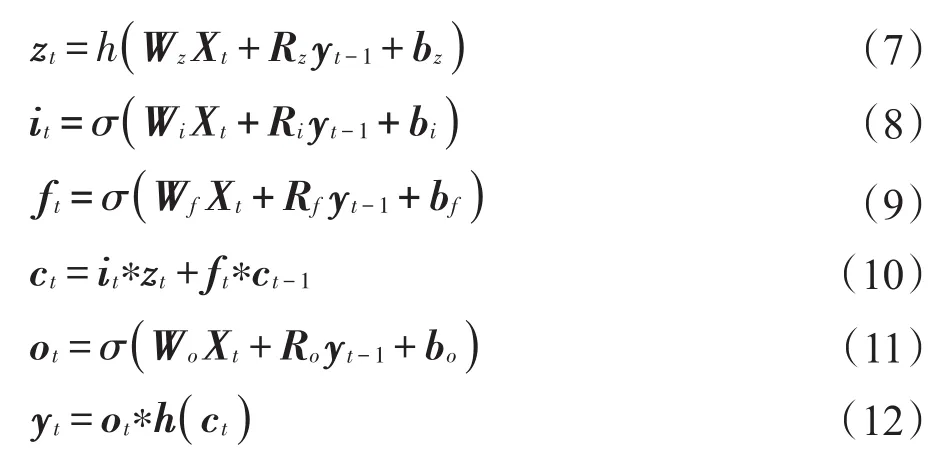
其中，逻辑Sigmoid函数σ用作门的激活函数，双曲正切函数tanh通常用作记忆单元输入输出激活函数h，符号∗表示按元素乘。

与输入的时间序列x1,x2,…,xn类似，LSTM神经网络的输出也是一个时间序列y1,y2,…,yn。针对运动想象EEG的分类问题，本文将输出序列在所有时间步上进行平均，得到最终的输出y，并将y输入一层全连接隐含层，其中隐含层的输出激活函数是tanh函数，如图3所示。

1.4 识别方法步骤

图3 LSTM分类模型Fig.3 LSTM classification model

本文基于运动想象EEG的空间频率与时间序列信息，提出一种多类运动想象EEG的特征提取方法，识别方法步骤如下：（1）首先将训练集原始EEG数据进行离散小波变换提取运动想象任务相关子带小波系数，接着利用OVR-CSP进行特征提取。对n类运动想象任务构建n个两类空间滤波器，并将其组成一个多类空间滤波器。（2）将训练集原始EEG数据通过滑动矩形窗（长度为1 s，重叠50%）提取出多段EEG，并将这些EEG数据段按照时间序列组成时间序列EEG。然后，对时间序列EEG中的每段信号进行离散小波分解，选取运动想象EEG相关频带的小波系数，将训练数据经过多类空间滤波器滤波并计算特征，从而得到降维的DWT-CSP时间序列特征。（3）将训练集的DWT-CSP时间序列特征作为LSTM网络的输入，在LSTM之后再添加一层全连接隐含层，将隐含层的输出输入Softmax分类器，得到训练集的分类结果。采用沿时间反向传播算法训练网络，反向传播包括两个方向：一个是沿时间的反向传播，即从当前时刻开始，计算每个时刻的误差项；另一个则是将误差项向上一层传播。（4）将测试集的EEG数据依次经过DWT、多类空间滤波器滤波和训练好的LSTM网络，从而得到时间步上平均的DWT-CSP-LSTM特征，特征经Softmax分类器得到测试集的分类结果。

2 实验及结果分析

2.1 实验数据描述

本文采用2005年BCI竞赛III-a数据集K3受试者脑电数据，该受试者执行4类运动想象任务，分别为左手、右手、脚以及舌头。实验使用美国Neuro公司的Neuroscan脑电采集设备，该设备包含64导联电极的脑电帽，以及采样频率为250 Hz的放大器。此外，该脑电采集设备将采集到的脑电数据以GDF格式存储。

该数据集的实验范式如图4所示。受试者处于相对安静的实验环境，并以较放松的状态坐在实验椅上。为了防止由于信息反馈对系统产生影响，所有任务的显示是随机的。当实验开始后，受试者需要保持安静，当t=2 s时，BCI系统发出响声提示受试者试验正式开始，此时系统显示器上出现一个“+”，提示受试者需要开始集中注意力。当t=3 s时，显示器上出现具有上下左右4个方向的箭头，其中上下左右方向分别与左手、右手、脚、舌头想象运动对应，受试者按照不同方向箭头做出相应的运动想象。该数据集箭头只保持显示1 s时间，因而在t=4 s，该箭头从显示器上消失，但受试者仍需保持执行运动想象任务直至t=7 s。

2.2 参数选取

图4 实验范式Fig.4 Timing of the paradigm

在基于空间频率和时间序列信息的特征提取中，需要确定DWT的分解层数，CSP特征提取时每类空间滤波器所选取的特征向量数目，以及LSTM神经网络隐含层数与每层单元数等参数，这些参数的选取将直接影响本文特征提取的分类正确率。本文采用训练样本数据5折交叉验证的方法来优化选取这些参数。

由于运动想象EEG的相关节律为α节律（8～12 Hz）和β节律（14～30 Hz），且该数据集的采样频率是250 Hz，本文选取Daubechies类db4小波，对每段EEG进行4层小波分解，各层子带频带范围如表1所示。从表1可以看出D3和D4子带的频率范围与运动想象EEG相关节律的频率范围相近，因而选取D3和D4子带的小波系数组成新的脑电小波信号[ ]D3,D4。

OVR-CSP算法则是构造多个空间滤波器，每个空间滤波器选择其中一类作为第一类，其余类作为第二类。因而每个空间滤波器可选择2m特征向量组成空间滤波器，或者选择第一类最大的m特征值对应的特征向量组成空间滤波器。K3受试者数据的分类正确率随m或2m变化的实验结果如图5所示。从图5可以看出，无论是由m或2m特征向量组成的空间滤波器，随着m值从1增大到16，各受试者数据的分类正确率都是按先逐渐增大，达到最大值后开始降低的趋势变化。但是由2m特征向量组成的空间滤波器在m=2时达到最大值92.23%，提取出的特征维数为16，而m特征向量组成的空间滤波器在m=7时达到最大值91.86%，提取出的特征维数为28，考虑特征维数和准确率两个因素，本文选取最优特征向量数m=2的2m特征向量组成空间滤波器。

表1 脑电信号4层小波分解Tab.1 Frequency band of electroencephalogram(EEG)signals using 4-layer wavelet decomposition

图5 K3受试者取不同m值时的分类准确率Fig.5 Classification accuracy of subject K3 in different m

LSTM神经网络选择合适数量的隐藏层没有一般规则，具有少量神经元的神经网络可能不足以对复杂函数建模。另一方面，具有太多神经元的神经网络可能导致网络过拟合，从而失去对测试集的泛化能力。找到最佳隐藏层数最常见的方法是实验和试错，不同隐含层层数和单元数的参数实验结果如图6所示。依据图6的对比实验结果，本文选择单隐含层25个LSTM单元的神经网络结构进行特征提取。

2.3 结果分析

图6 LSTM单元数对分类精度的影响Fig.6 Effect of the number of LSTM units on classification accuracy

本文应用基于空间频率和时间序列信息的特征提取方法在BCI竞赛III中Dataset III-a的K3受试者数据集上进行4类运动想象任务分类测试实验。图7为CSP、DWT-CSP算法提取受试者K3的特征分布图，为了对特征进行可视化，本文只选择由左手想象运动与其余想象运动形成的空间滤波器提取的一组二维特征，从图7可知，单独采用CSP算法从3名受试者脑电数据得到的特征类别间区分度较小。而经过DWT-CSP方法得到的特征可以看出具有较为明显的差异性，这说明频率信息能够增大类别间的区分度。当采用更加完备的特征向量时，不同类别间的差异性会更加明显。

为了进一步探索空间、频率以及时间序列信息对于运动想象EEG分类性能的影响，本文还对CSP特征、DWT-CSP特征以及CSP-LSTM特征与本文算法基于相同Softmax分类器的分类结果进行对比，如图8所示。其中，单独采用CSP算法准确率为78.33%，而结合空间与频率信息的DWT-CSP特征的分类准确率达到85.55%，结合空间与时间序列信息的CSP-LSTM特征的分类准确率达到84.96%，这说明频率或时间序列信息对于运动想象EEG分类的有效性，并且本文算法的分类准确率达到了92.23%，进一步说明空间、频率、时间序列信息之间的互补性。

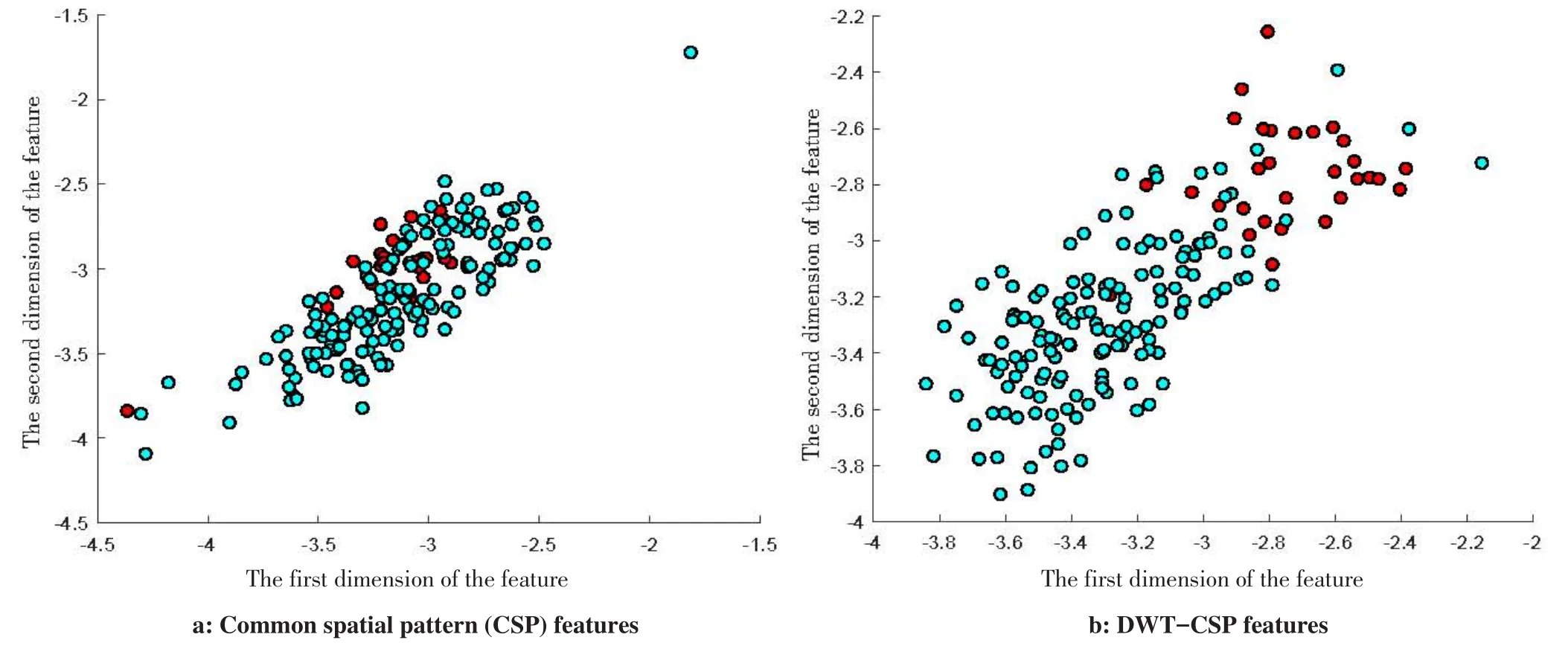
图7 CSP、DWT-CSP算法提取受试者K3的特征分布图Fig.7 Distribution of CSP and DWT-CSP features of subject K3

图8 二维特征分布Fig.8 Two-dimensional feature distribution

最后，将本文所提出的方法与其他文献中方法所得的分类准确率进行对比。文献［19］结合CSP与CNN神经网络进行特征提取，并采用Softmax分类器进行分类，正确率达91.46%；文献［20］采用CSP方法进行特征提取，并应用设计的BP神经网络对提取的特征数据进行分类，正确率达76.67%；文献［21］是基于CSP、Hilbert变换和SVM的特征提取与分类算法，准确率达91.11%。可以看出，本文所提出的方法分类正确率比其他文献有所提高，准确率达92.23%。

3 结论

从非线性、非平稳的运动想象EEG中提取特征是BCI系统的关键环节，针对在多类运动想象EEG分类时，CSP特征提取方法缺少频率和时间序列信息的问题，本文将CSP方法与DWT、LSTM神经网络算法结合起来对多类运动想象EEG进行特征提取，并采用Softmax分类器进行任务分类。在2005年BCI竞赛III-a的K3的4类运动想象脑电数据集上，相比单独采用CSP、DWT-CSP、CSP-LSTM方法，融合空间、频率、时间序列三者信息的DWT-CSP-LSTM方法达到了更好的分类结果，表明空间、频率、时间序列信息的互补性和有效性，为BCI系统中EEG的特征提取提供一条新的思路。