一种求解NP-难问题的并行协同大规模差分进化算法
2019-01-24张峰
张 峰
安徽交通职业技术学院航海系,合肥,230051
1 引言
随着科学技术的发展以及大数据时代的到来,优化问题的规模日益增长,因而也给当前主流的优化算法带来了严峻挑战。NP-难问题在人们实际生活中随处可见,比如,随着中国城镇化建设速度越来越快,大城市的交通流畅性问题越来越严重,如在大城市中合理布局公交站点问题。站点和路线的选择都是从上千乃至上万甚至上十万的候选点以及候选路线中筛选的,因此这种站点优化以及路线优化问题均属于一种大规模优化问题[1]。
随着NP-难问题规模的增大,数据维度的剧增,使得待优化问题的维度越来越高,优化算法的搜索空间呈指数式增长,大大降低了传统优化算法的搜索效率[2]。另外,数据量的激增使得待优化问题的复杂度越来越大,大大增加了优化算法的执行时间,虽然可以通过计算机穷举算法来解决这种问题,然而当问题的规模逐渐扩大时,这些算法也逐渐失效,因为这些实际问题本身就是一种NP-难问题,当问题规模变大时,计算机穷举算法很难在人们可接受的时间范围内给出一个可靠或者理想解。
进化算法又称为计算智能算法,为求解以上问题提供了有效解决途径。但尽管传统进化算法已经在低维空间中获得良好的效果,然而,随着问题维度的增加,传统进化算法的可行性及有效性遇到极大挑战。因此,为了有效解决大规模优化问题,新型大规模优化算法亟须被提出。虽然目前已经有很多协同进化算法被提出,但是现有的协同进化算法主要着眼于维度分组算法的研究,并且大都采用串行方式,执行效率低是当前协同进化算法主要面临的瓶颈[3]。因此,为了提高进化算法的执行效率,本文提出了一种求解NP-难问题的并行协同大规模差分进化算法,基于现有的维度分组算法提出了一种改进维度分组算法,从而将高维度优化问题降解为多个低维度的子问题,从而能够获得更加准确的分组;其次,针对获得的维度分组,独立优化每个子问题,最后在CEC’2010数据集上进行大量实验,验证本文提出的并行协同进化算法对于求解NP-难问题的有效性。
2 相关研究综述
为高效求解NP-难问题,美国的Holland教授借鉴生物界的进化规律,基于达尔文的进化理论提出了遗传算法(Genetic Algorithm)来求解NP-难问题。因此,在短期内大量的改进版的遗传算法被提出,而且被应用于各个领域,比如电力系统调度、云计算、车辆调度、机器学习等[3,4]。随着研究的深入,各种智能演化算法相继出现,比如分布估计算法、人工蜂群算法、烟花算法等。这些算法随后被用于求解各种优化问题,比如多目标优化、多峰优化和动态优化等[5-7]。
目前,大规模优化算法研究主要分为两个大方向:其一,提出新的整体式进化算法,包括基于反馈机制的PSO算法(FBE)、基于竞争机制的群体智能算法(CSO)等。其二,提出新的协同进化算法。协同进化算法是一种基于分治算法的智能进化算法,其主要思想是将高维问题分解为多个低维问题,再将每个低维问题视为独立的子问题。主要的分组算法有随机分组(RG)、Delta分组(Delta-G)、多层随机分组(MLCC)和差分进化分组(DG)等[8-10]。
一方面,虽然现有的而且比较流行的整体式优化算法已经在高维度问题上获得了比较好的优化效果,但是这些算法在多峰问题上却表现较差,主要是受到了大量的局部最优解的影响。另一方面,目前的协同进化算法都是串行实现,往往需要较长时间的运行才能得到最终结果。因此,如何在广袤的搜索空间中高效快速地寻找大规模优化问题的最优解仍然是比较棘手的问题。如何有效地平衡进化算法的多样性与收敛速度是求解大规模优化问题的关键。
3 求解NP-难问题的差分进化与大规模优化算法
3.1 差分进化算法
差分进化算法(differential evolution, DE)是一种基于种群的进化算法,自1997年被Storn和Price提出之后,越来越多的研究者们将注意力集中于DE的研究,并提出了多种DE的变种算法。DE算法大致包含四个组成成分:初始化、变异算子、交叉算子和选择算子。交叉算子中的二项交叉因其简单有效,参数容易设置等特点,已经成为一种主流的交叉算子,并被广泛应用于DE的各种变种算法[11]。
3.2 大规模优化算法
3.2.1 整体式进化算法
传统进化算法在求解高维优化问题时失效的原因是难以在探索能力和开发能力中寻求一个好的平衡点。一个进化算法的多样性往往取决于所使用的学习策略或者更新策略。因此,为了更好地求解高维度优化问题,提出了许多新的学习机制或者更新策略。
Cheng等提出了一种竞争学习机制[12,13],将该学习机制结合不同的双亲选择机制,提出了不同的粒子群进化算法。该算法中,各粒子都不向自己的历史最优解(pbest)以及种群的历史最优解(gbest)或者各自的最优近邻(lbest)学习,而是向当前种群中较优的粒子学习。在种群进化过程中,特别是在进化阶段的后期,pbest,gbest,或者lbest可能在连续几代中维持不变,因此,它们对维持种群的多样性不利。
3.2.2 协同进化算法
协同进化算法是由Potter教授在1997年提出[14],基于分治算法,将大规模问题通过维度分解的方法分为许多维度小的小规模问题,再对每个小问题使用传统进化算法单独进化,进化完成后,将各个子问题优化得到的最优解结合起来,即得到原问题。
3.2.3 维度分组策略
目前的维度分组算法主要分为两大类:动态分组和固定分组。动态分组是一个动态过程,最基础而且最简单的动态分组算法就是随机分组。固定组数的随机分组虽然组数是固定的,但每个组的组成成分却是不固定的。固定组数的随机分组最大的缺点是需要提前设置好分组数[15,16]。
动态组数的随机分组的主要策略是事先定义一个组数的集合(假设r为集合S的大小,其中的每个元素都代表一个分组数目),而后在每次随机分组前,事先都从集合S中随机选取一个元素作为分组的数目,而后再根据这个选择的分组数对维度进行随机分组。起初从集合S中选择组数的机制是随机机制,明显地,动态分组算法将变量之间的关联信息当作局部信息,因此维度的分组也在优化过程中动态调整[17]。
4 基于维度分组的并行协同大规模差分进化算法
为了提高并行进化算法的运行效率,本文依托新提出的维度分组策略提出了基于维度分组的并行进化算法——并行协同进化算法。不同于传统的协同进化算法顺序优化子问题,在该算法中,每个维度分组视为独立子问题,而后算法同时优化每个子问题。
4.1 算法的基本设计
在基于维度分组的并行协同大规模差分进化算法中,每个进程负责优化一个或者多个维度分组(子问题)。该算法的主要框架如图1所示。由图1可知,本文提出的并行算法框架是一种主从式并行算法设计。
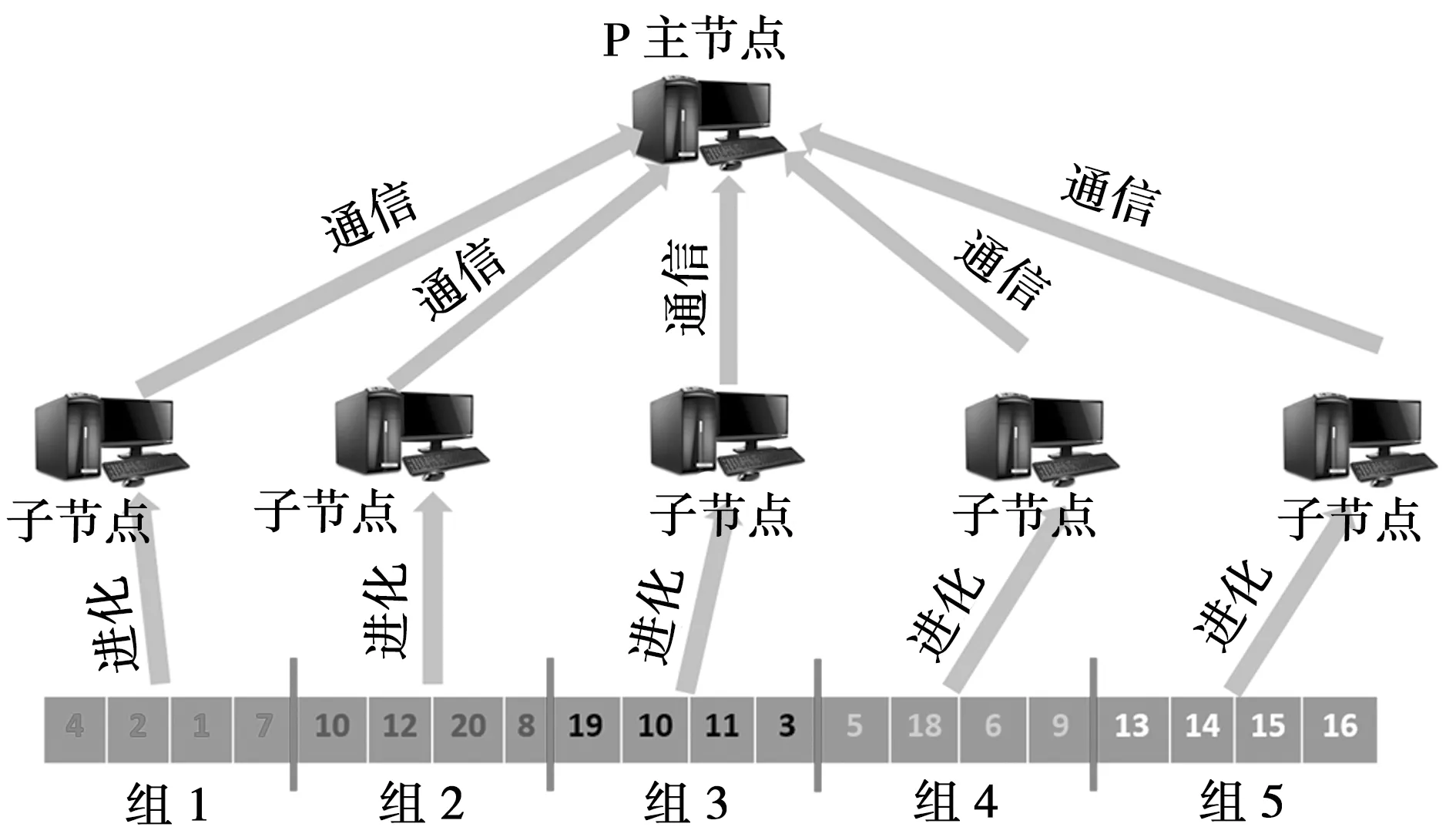
图1 基于维度分组的并行协同进化算法框架
根据图1所示的协同进化算法框架,在优化每个子问题时,负责该子问题的子种群需要将种群其他分组维度设定为目前全局最优解所对应的值,因此,每个子进程需要获得全局最优解信息。而主节点对应的主进程主要有两个任务:搜集各个子问题所优化得到的全局最优解,然后拼凑在一起,得到整个问题的最优解;将搜集得到的整个问题的最优解广播到每个子进程,以便每个子进程获得最新的全局最优信息。而每个子节点对应的子进程则只需要不断进化子种群,并定期将进化得到的最新的最优解传递给主进程。
在并行算法中,主要的时间耗费应该集中于子问题的不断优化,所以好的并行算法应该尽量减少通信时间的开销。因此采用改进的差分分组算法可以大大减少通信开销,提高了并行算法的执行效率。
4.2 并行差分进化算法的实现
基于维度分组的并行协同大规模差分进化算法的并行框架是一种异构进化策略。并行协同进化算法则只有等到主进程搜集到所有的子种群进化得到的部分最优解之后,将各部分拼凑起、广播出去,子进程才能利用到最新的全局最优解信息,这是一种异步进化策略。在后续实验中,分析和对比并行协同的异步进化策略与顺序协同的同步进化策略,分析两种进化策略对协同进化算法的影响。本文提出的并行协同进化算法的伪代码如算法所示。
算法:并行差分进化算法
输入:维度分组G={G1,G2,…,Gm},分组个数m,计算机核数n;种群大小NP;最大迭代次数Max_Iter;
1:将0号进程设为主进程,其余(n-1)个进程设为从进程,负责优化每个分组;
2:每个从进程负责优化的分组个数L=m/n;
3:If(m%n≠ 0)
4:前m%n个从进程负责的分组数为L=L+1;
5:End If;
6:主进程初始化gbest;
7:每个从进程初始化自己的种群;
8:iter= 0;
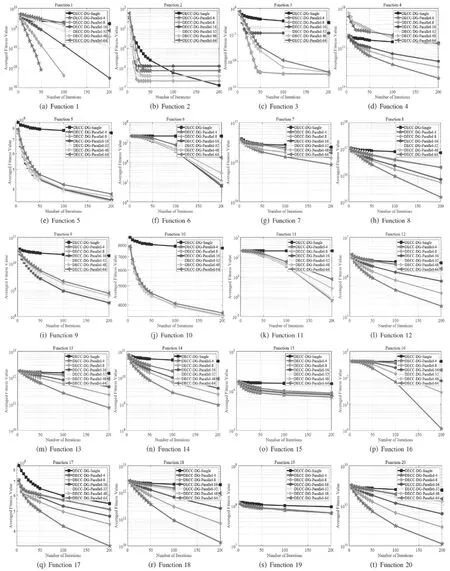
9While(outer_iter 10:主进程广播gbest到每个子进程; 11:Fori= 1:n 12:Forj= 1:L 13:While(inner_iter 14:第i个子进程优化所负责的第j个分组; 15:inner_iter++; 16:End While 17:End For 18:第i个子进程发送优化好的所负责的所有分组的gbest; 19:End For 20:主进程接收每个子进程发送的gbest,并拼接为新的new_gbest 21:If(f(new_gbest) 22:gbest=new_gbest; 23:End If; 24:outer_iter++; 25:End While; 输出:gbest及其对应的适应值f(gbest); 本文提出的算法需要的通信时间较少。这是因为在早期的并行算法中,主进程必须将一个或者多个个体信息传递给子进程,而后子进程负责计算适应值。而本文中的并行算法中,主进程只需要将gbest传递给各个子进程,同时每个子进程只需传递各自优化得到的gbest的部分给主进程,因此本文提出的并行算法所需要的通信量大大减少。 另外,还可以看出,在早期的并行进化算法中,子进程只负责适应值的计算,而主进程负责个体的更新。然而在本文提出的并行进化算法中,子进程维护一个子种群,用来优化一个或者多个子问题。而主进程只负责收集各个子进程的优化得到的gbest信息。子进程不仅仅负责适应值的计算,而且负责子种群的更新;而主进程只负责收集和广播信息。因此,本文提出的并行算法并行度更高。 本研究用C++语言基于MPI并行环境实现本文提出的并行算法框架。主进程的任务主要有两个:(1)收集各个进程发送过来的各自优化得到的gbest分量,并将它们整合成为一个完整的gbest值,并更新当前找到的历史最优解;(2)将更新过的gbest广播给每个子进程,进入下一轮优化。首先,子进程接收主进程广播的历史最优解;而后利用SaNSDE算法进行迭代优化;最后在优化一定代数后,将优化得到的最优解传递给主进程。 4.3.1 实验环境设计 本研究首先实现了基于改进同进化算法应用在当今比较流行而且被人们广泛使用的大规模优化基准函数库——CEC’2010基准函数库。该函数库包含20个1 000维的大规模优化问题。这20个函数的主要特点如表1所示。 表1 20个CEC’2010函数的主要特性 本研究将种群大小NP设为50,每个子种群迭代次数设为40,即算法的内层循环次数Inner_Max_Iter= 40;整个种群的迭代次数设为200,即外层循环次数Outer_Max_Iter=200。为了保证实验的公平性,每个算法都独立运行30次,实验结果取这30次独立实验的平均值。为了后续描述,本文将顺序协同进化算法表示为“DECC-DG-Single”,而将并行协同进化算法表示为“DECC-DG-Parallel”。 同时,为了研究分配的计算机核数对本文提出的并行协同算法的影响,在实验过程中,在不同的核数下运行本文提出的并行协同进化算法。不同核数下的并行进化算法可以表示为“DECC-DG-Parallel-m”,其中m表示所分配的核数。比如基于4核的并行进化算法可以表示为“DECC-DG-Parallel-4”。另外,顺序和并行协同进化算法都运行在相同配置的机器上,每台机器的配置为4 个Intel(R) Core(TM) i5-3470 3.20GHz CPU,4Gb 内存和64位的Ubuntu 12.04 LTS操作系统。其中顺序协同进化算法独立运行在一台机器上,并行算法最多运行在16台机器上,也就意味着本文中并行算法的最大核心数为64。 4.3.2 结果分析 为了探索不同核数对并行协同进化算法的影响,本研究将实现的并行协同进化算法分别分配4核、8核、16核、32核、48核以及64核进行并行实验,图2展示了串行协同进化算法和并行协同进化算法在进化过程中获得的函数值对比结果。 值得注意的是,图2(a)中,基于4核和8核运行的并行协同进化算法(DECC-DG-Parallel-4和DECC-DG-Parallel-8)分别在50和100代后在图中没有了显示结果,这是因为DECC-DG-Parallel-4和DECC-DG-Parallel-8分别在50和100代后得到了该函数的最优值——0。从该图可以得出以下结论: (1)当函数的分组数大于最大核数64时,随着核数的增加,在大部分函数上,DECC-DG-Parallel的表现越来越差。 比如在F1,F6,F7,F13,F18,F20等函数上,DECC-DG-Parallel-4表现最好,但是随着核数的增加,DECC-DG-Parallel表现越来越差,当核数增加到64时,DECC-DG-Parallel表现最差。这是因为核数的增加,使得每个子进程负责的分组数减少,从而使得子进程内部的同步通信减少,也就意味着并行间的异步通信程度变大。过度的异步通信,使得算法的收敛速度变慢,从而使得算法的性能下降。 (2)除了F2外,并行协同进化算法几乎在所有的函数上都明显好于串行协同进化算法。 具体来说,在不同核数下的DECC-DG-Parallel都明显优于DECC-DG-Single,特别在F1,F3,F5,F6,F8-F11,F14等函数上,DECC-DG-Parallel大大优于DECC-DG-Single,而且在F1上,DECC-DG-Parallel-4 和DECC-DG-Parallel-8都能够优化到函数的最优值——0。这也就意味着并行协同进化算法的异步通信策略大大优于串行协同进化算法的同步通信策略。这是因为同步通信策略往往太贪心,容易使得算法陷入局部最优。 (3)DECC-DG-Parallel-4在大部分函数上表现最好。 具体说来,DECC-DG-Parallel-4在F1,F4,F7,F8,F12-F14,F16-F18,F20函数上表现得明显比其他任何核数下的DECC-DG-Parallel和DECC-DG-Single都要好。从收敛速度方面来看,与DECC-DG-Single相比较,在不损失所得解的质量甚至获得更高质量解的前提下,DECC-DG-Parallel几乎在所有的函数上获得更快的收敛速度。 (4)在F8,F14-F17上,DECC-DG-Parallel-32,DECC-DG-Parallel-48和DECC-DG-Parallel-64得到相同的效果。 在F19上几乎所有核数下的DECC-DG-Parallel都获得了相同的表现。这是因为在F8,F14-F17上,当核数大于等于32时,此时的核数超过了函数的最大分组数,因此只有等于最大分组数的进程才真正起进化子种群,并且这些进程都只优化一个函数分组,而其他进程则空闲。在F19上,由于只有一个分组,因此在该函数下只有两个进程起作用,一个是主进程,一个是子进程,并且该子进程负责优化整个函数(因为该函数只有一个分组)。因此,可以得出并行协同进化算法大大优于串行协同进化算法,也证明了对于协同进化算法,并行环境下的异步通信策略大大优于串行环境下的同步通信策略。但是这种异步通信并不是异步程度越高越好。过度的异步通信使得算法收敛速度变慢,算法的性能下降。 图2 DECC-DG的串行实现(DECC-DG-Single)和并行实现(DECC-DG-Parallel)之间的对比结果 以上通过实验验证了并行协同进化算法在解的质量方面大大优于串行协同进化算法。为进一步体现并行协同进化算法的优势,本文将从算法运行时间方面来验证并行协同进化算法的优势。对于并行算法,研究者们往往关心并行算法相对于串行算法的加速比,其定义如下: (1) 其中,TSingle是串行算法的运行时间,TParallel是并行算法的运行时间。图3展示了DECC-DG-Parallel相对于DECC-DG-Single的加速比随着核数增加的变化情况。 从该图可知:当函数的分组数大于最大核数(64)时,比如F1-F3,F9-F12,随着核数的增加,并行算法的加速比也在增加,而且这种增加接近线性。虽然核数是呈指数增加,但是并行算法的加速比往往不会呈指数增加,而是呈接近线性增加,这是因为并行算法中的各个子进程需要通信,需要消耗一定时间,另外,主进程在收集子进程发送的信息时需要一定的等待时间。 图3 不同核数对并行协同进化算法加速比的影响 对于F8,F14-F17,当核数超过32时,加速比不再增加,这是因为这些函数的最大组数都少于32,当核数超过32时,只有等于组数个数的进程在工作,而其他进程则处于空闲状态。因此,此时并行算法的时间不会再有缩短,从而导致并行算法的加速比保持不变。对于F19,发现在该函数上并行算法的加速比呈下降趋势,但是这种下降不是很多,只是降低了少许。这是因为F19只有一个分组,当创建大量进程时,实际上只有两个进程在工作——一个主进程,一个子进程。 本文提出了一种求解NP-难问题的并行协同大规模差分进化算法,从而将高维度优化问题降解为多个低维度的子问题,进而能够获得更加准确的分组;其次,针对获得的维度分组,独立优化每个子问题。求解NP-难问题的并行协同大规模差分进化算法有以下优点:(1)通信量小。种群式并行方式需要传递一个或者多个个体给节点,而维度分块式并行只需要传递维度分块信息给每个节点,因此通信信息远远小于种群式并行;(2)并行粒度大,可扩展性强。维度分块式并行方式取决于维度,与优化问题直接相关,随着维度的增加,维度分块越多,并行粒度也就相对较大;而种群式并行方式跟种群相关,该方式下的并行粒度最多与种群大小相同。 最后,通过大量实验论证了并行协同进化算法大优于串行协同进化算法。结果表明,随着核数的增加,并行协同进化算法的加速呈近线性增加,而其获得的解的质量却在下降。说明加速比的提高与解的质量提高存在着冲突。因此,为了使并行协同进化算法的性能最大化,应该在加速比和解的质量之间寻求一个最佳平衡。4.3 实验结果

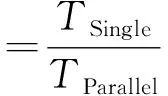

5 结 论
