建筑物泄爆结构风险设计方法*

2019-01-24王明洋高康华邱艳宇

湘潭大学自然科学学报 2018年5期

卢浩，王明洋，高康华，邱艳宇

(陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏南京 210007)

泄爆设计是有气体(粉尘)爆炸危险的厂房、仓库广泛采用的防爆方法之一.关于泄爆现象和机理的研究成果较多[1-2]，美国消防协会NFPA68-2013[3]、欧洲标准协会EN14994-2007[4]以及中国国家标准GB50016-2014[5]分别给出了泄压设计标准，提出了泄爆面积计算公式.上述标准都是在给定爆炸灾害水平下满足给定性能的要求，简单易行，但不能充分体现爆炸灾害自身的随机性以及破坏后果的不确定性.建筑物内气体爆炸是发生概率很低的风险事件，根据近年来天然气用户总量以及事故统计数据[6]，我国城市燃气事故率为1.6～2.6起/百万人，按最不利情况进行设计必然会大大降低经济效益，造成计算结果偏保守，按确定性理论进行设计难以考虑后果的不确定性.

风险设计已在桥梁安全设计、大坝设计、核安全等多个领域得到发展和应用.陈艾荣等[7]基于风险理念提出了考虑灾害危害性和桥梁多级性能水平的抗灾设计方法；刘光文[8]提出以风险率为基础的防洪安全设计方法；肖义等[9]建立了可接受风险水平约束下的大坝防洪安全标准的风险决策模型；美国在多个安全标准制定中采用了风险管理的理念.在气体爆炸风险方面也开展了一些研究.Weerheijm等[10]针对隧道内气体爆炸事故开展定量风险分析；Junaid Hassan等[11]给出了粉尘爆炸发生概率的评估模型；王若菌等[12-13]针对蒸气云爆炸事故存在的不确定因素，建立了蒸气云爆炸风险评估模型.风险设计是目前抗爆研究的重要方向，目前针对建筑物内爆炸风险发生概率、爆炸荷载不确定性、爆炸风险可接受标准等一系列问题相关研究成果较少，尚未形成一套基于风险的泄爆设计方法.

本文引入风险分析方法，将爆炸事件处理成风险事件，从概率的角度出发，深入分析爆炸事件发生概率、爆炸毁伤概率，根据可接受风险水平指导建筑物泄爆设计，形成了一套建筑物爆炸安全风险评价方法，指导泄爆结构的优化设计.

1 风险设计理论

1.1 不确定性分析

建筑物内爆炸影响因素复杂，不确定性强，主要体现在：

(1) 影响因素既有人的不安全行为，又有物的不安全状态，以及环境因素等，这些因素都具有相当大的不确定性，导致事故的发生具有随机性[14].

(2) 爆炸强度的不确定性，爆源的种类、组分及浓度、初始压力、温度、点火源位置、点火强度、爆室空间特性、内部障碍物的布置与位置、泄放结构型式、面积、开启规律等因素都会影响爆炸荷载的大小，在针对某一特定建筑物进行爆炸危害性评估时，爆源的种类、爆室空间特性、内部障碍物、泄放结构、初始压力、初始温度等因素是基本确定或变化不大的，造成爆炸超压值不确定性的主要因素是气体浓度、点火源位置、点火强度，而这些因素对爆炸荷载影响显著，必须考虑其随机性.

(3) 爆炸后果的不确定性，爆炸影响范围内人员的数量、结构抗力参数、人员抗力水平的随机性都会造成损失的不确定性.

对风险事件中不确定的合理描述和科学表征是风险分析的重要步骤.概率提供了相应的数学结构形式，对于事故发生的不确定性，可以描述为：

P(A)=f1[P(X1)，P(X2)，…，P(Xn)].

(1)

式中：P(A)为爆炸事件A的发生概率；Xi为影响事件发生的第i个基本事件；P(Xi)为第i个基本事件的发生概率；f1为第一个算子.

对于爆炸强度的不确定性，可以用概率分布来表征：

f(φ)=f2[f(x1)，f(x2)，…，f(xn)]，

(2)

式中：f(φ)为表征爆炸强度的随机变量φ的概率密度函数，xi为影响爆炸强度的第i个因子，f(xi)为第i个因子的概率密度函数.

对于爆炸后果(人员、结构)的不确定性，可以用下式来表征：

P(Ci,j)=P(Ri,j-S<0)，

(3)

式中：P(Ci,j)为事故发生条件下第i种损失第j种损伤状态的发生概率；Ri,j为造成第i种损失第j种损伤状态时抗力的随机量；S表示作用荷载效应的随机量.

1.2 风险计算模型

卡普兰将系统相关的风险描述为三相量的集合：

(4)

式中：R为风险，Ai是事件集，Pi是事件频率集，Ci是事件后果集.

评估风险大小，不仅考虑风险发生的频率，还要分析风险对个体、社会或环境造成的损失，为了将风险数量化，可将风险看作爆炸影响范围内遭受损失的数学期望值[15]：

(5)

式中：φ用来描述爆炸事故的强度；Sr为积分域(主要是爆炸影响范围)；φmin、φmax表示爆炸强度最小值和最大值；P(φ)表示在参数φ的影响下损失概率；ψ(x,y)为爆炸范围内人员设施分布；f(x,y,φ)为坐标(x,y)范围内参数φ的分布情况.

1.3 风险接受标准

风险接受标准的选择本质上就是风险决策问题，涉及安全性与经济性的平衡，不同风险接受标准对应不同的安全风险以及工程经济关系，最优泄爆设计方法应能使防爆安全标准提高所耗费的投资可从破坏发生时减少的风险损失中得到最大的补偿.国际上目前普遍使用的风险管理准则是ALARP原则，该原则将风险划分为3个区域：不可接受区域、ALARP区和可接受区.基于该原则，2014年我国大陆地区颁布了《危险化学品生产、储存装置个人可接受风险标准和社会可接受风险标准》(以下简称《标准》)，规定了个人风险可接受风险标准、社会可接受风险标准.

后果包括经济损失、社会影响、人员伤亡等，风险接受标准的制定要考虑后果的种类和统一，《标准》中仅考虑了人员死亡率.从爆炸事故案例统计结果看，相比于经济损失，人员伤亡往往更能反应事故的严重程度，并且人员伤亡会产生更大的社会影响，利用人员死亡率制定风险接受标准是合理的，具体形式为：

(6)

式中：P(D1|φ)为参数φ的影响下人员死亡概率；f(φ)为参数φ的概率分布密度；RP,u为个人可接受风险标准；RS,u为社会可接受风险标准尽可能降低区的上限.

在满足上述风险接受标准的基础上可采取费用-效益进行设计优化.

2 风险计算方法

2.1 发生概率计算

计算爆炸事件发生概率通常思路是通过识别、分析事件的可能原因，建立事件和可能原因之间的逻辑关系，最后通过计算因素发生概率来确定事件发生概率，目前常用的方法有因果图、故障树分析、贝叶斯网络等，其中应用最广泛的是故障树分析.对于事故统计资料比较完善，统计数据健全的系统来说，故障树分析能够较全面分析事故原因、发生路径，并可通过基本事件的概率得到顶事件(危险事件)的发生概率，具有较强的可信性.然而，对于大多数爆炸事件来说，影响因素多，因素之间的关系获取难度大，基本事件统计数据缺乏，这就导致故障树路径不完整，受基本事件统计信息的影响，顶事件概率可信性不强.鉴于此，基于观测统计法的事件概率计算方法在当前得到广泛的应用.

表1为2011-2017年度燃气事故数、用气人口、事故频率统计，从统计表可以看出，我国用气人口在增加，燃气事故比例在下降，事故频次为4.3×10-6～8.2×10-6.表1中数据包含了民用、工业、商业、交通等，对于各类建筑物比如工业厂房、仓库没有相关的统计数据.在开展具体建筑物发生概率计算时，可以利用统计频次乘以相应的风险控制系数，并结合具体建筑物爆炸的危险性得出，即

(7)

式中：Pa为事故发生频次统计最高值，根据表1中统计数据，可取1×10-5；K1为风险控制系数，根据防护目标的危险性进行设定，参考国外在确定可接受风险标准中的做法，分别选定10%、1%应用于不同防护目标，其中10%应用于危险性较小的民居类建筑，1%应用于危险性较大的有爆炸危险的工业厂房、仓库类建筑；K2为当前建筑物爆炸危险性指数，在进行新建建筑物泄爆设计时，可取1，在进行已建建筑物爆炸评估时，可根据与同类建筑物相比当前建筑物的危险性进行调整.

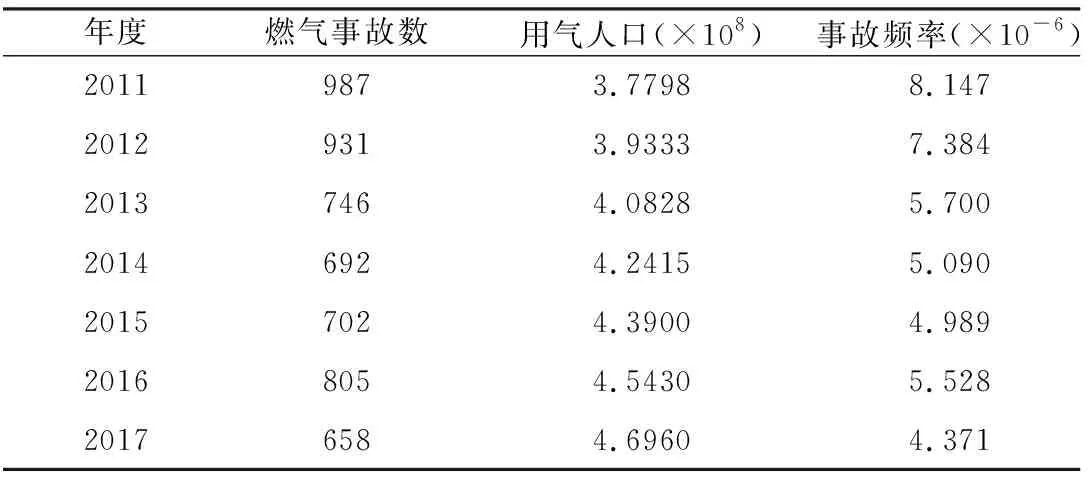
表1 2011-2017年度燃气事故数、用气人口、事故频率统计

注: (1) 燃气事故数据主要来自博燃网，2011-2014年度用气人口数据来源于住建部编写的《中国城乡建设统计年鉴》，2015-2017年度根据前几年度的数据拟合预测得出.

(2) 事故频率=事故数量/用户数量，用户数量根据用户人口与每户平均人口计算得出，根据统计每户平均人口在3.1左右.

2.2 损伤概率计算

气体爆炸对人员的直接伤害因素有冲击波、碎片冲击、烧伤等，发生爆炸时车间、库房存放有易燃物时，还会造成火灾，造成人员烧伤；高空作业人员受冲击波或震荡作用，造成高空坠落；爆炸导致建筑物坍塌时，也会导致人员伤亡.本文仅考虑爆炸波所产生的伤害方式：冲击波和建筑物坍塌.

(1) 爆炸强度概率分布.俄罗斯科学家彼留金[16]通过对大量实验数据的分析，考虑屋室构造、尺寸、泄爆构件类型及分布规律等因素对准静态压力的影响，给出了准静态超压的计算公式：

(8)

式中：μH为火焰基本燃烧速度，与可燃气体种类有关，由实验测得；αz表示湍流增强因子，可以根据爆炸室内设备和建筑结构的阻塞比θ3和可燃混合物燃烧产物所占的爆炸室容积V确定；εc为计算增压比，由燃气化学性质决定，由实验测得；βμ表示考虑可燃混合物充填程度对压力的影响，一般取1；KB表示考虑爆室形状对压力的影响；VB是爆炸屋室的净空容积，m3；ρ0是爆炸前腔体内气体的初始密度，kg/m3；Ab.i表示i型泄爆构件的面积；Kj.i表示i型泄爆构件的击穿系数，该系数表示泄放构件击穿对于室内荷载形成的影响，其取值范围为0≤Kj≤1，通过大量实验，确定了玻璃、楼板、隔墙等常用构件在不同泄放压力及空间分布条件下的击穿系数.

文献[17]通过研究爆炸后果分布形式，运用案例统计方法反推出气体爆炸荷载的可能分布规律，结果表明单室荷载分布符合截尾正态分布形式，该结论与气体爆炸超压试验统计结果相符：

(9)

式中：f(Δp)是概率密度函数，μΔp是超压分布期望值，σΔp是超压分布标准差.得到超压分布期望值与标准差的计算公式：

μΔp=0.72Δpm，σΔp=0.23Δpm.

(10)

根据式(8)～(10)，考虑理论计算超压在计算过程与实际超压的差异，设计超压值可在计算超压的基础上乘以设计安全系数，即

Δpm,k=kpΔpm，

(11)

式中：Δpm,k为设计超压值，kp为设计安全系数.

(2) 冲击波导致的人员伤亡概率.国内外多名学者给出爆炸冲击波对于人员的伤害估计标准，主要采用超压值作为评价指标，如表2所示.

表2 爆炸冲击波对于人员的伤害估计

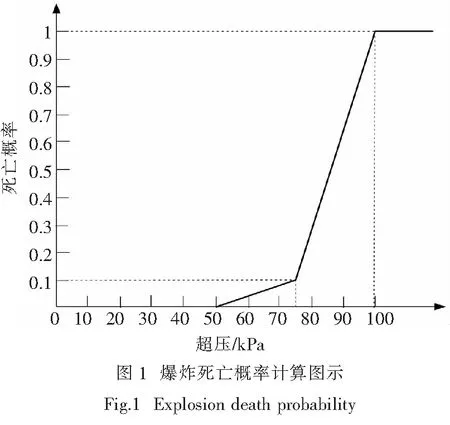
表2中分级标准具有一定的随机性，比如当人员承受超压值为70 kPa时，既有重伤的可能性，也有死亡的可能性，采用概率的方法进行处理，图1为根据表2中数据给出的以超压为指标的人员死亡概率曲线，概率曲线从中位数75 kPa处分为两段，50～75 kPa段死亡概率远远小于75～100 kPa，当超压为75 kPa，认为死亡概率为0.1，当超压为100 kPa，认为死亡概率为1，相对于表中数据，为安全起见，图中死亡概率曲线偏保守.

(3) 建筑物倒塌导致的人员伤亡概率事故案例表明[13,21-22]，砌体结构建筑物由于承载能力低，内爆事故中结构坍塌是人员死亡的主要因素，计算人员死亡率时必须考虑，而框架结构中由于主体结构承载力大，在爆炸事故中一般以局部破坏为主，不会发生整体坍塌，计算人员损失时可不考虑结构坍塌造成的人员伤亡.目前关于内爆条件下建筑物倒塌与人员伤亡之间的关系研究很少，关于房屋倒塌率与人员死亡率之间的关系主要集中在地震灾害后果分析中，结合内爆事故特点以及地震灾害研究成果，初步给出内爆条件下建筑物倒塌造成人员伤亡的估计方法.

尹之潜等[21]将地震死亡人员数据信息处理整合，并以房屋结构类型为根据，得出了房屋倒塌率与地震人员死亡率的表达关系式，与地震造成建筑坍塌继而导致的死亡率相比，内爆事故应更为严重.一方面因为内爆事故的突然性更强，事故发生时几乎没有反应时间；另一方面内爆冲击波压力会造成人员的受伤，在受伤状态下房屋倒塌造成人员的死亡率会更高.为此在地震经验公式[21]的基础上增加危险性系数KFR,即

(12)

式中：FR为人员死亡率，CR为房屋倒塌率.

为评价建筑物整体倒塌情况，可采用破坏系数KL来评估内爆事故时建筑物可能的坍塌情况.若KL=0，实际上就排除了发生严重破坏的可能性；若KL=1，则建筑物将完全破坏.

(13)

式中：Pi是发生爆炸事故时因承载结构破坏导致第i块楼板塌落的概率；SL,i是因承载结构破坏导致的楼板塌落面积；n是所有计算楼板的数量；SL,ALL是所有楼板的总面积.

Pi的值可通过承载结构的破坏概率以及承载结构的破坏对于建筑物整体的影响分析得出.承载结构破坏概率为：

(14)

式中：R表示结构抗力的随机量，通过作用形式以及结构参数来确定；S表示作用在结构上荷载效应的随机量，气体爆炸作用下用Δps=ΔpKd来表示，Kd为动荷系数.

3 实例与分析

以某框架结构厂房氢气爆炸为例，爆室尺寸长、宽、高分别为33 m、24 m 、12 m，室内设备和建筑结构的占有率θ2=10%，其中50%是小尺寸的设备和建筑结构，其余50%是大尺寸的，室内净空为8 554 m3，爆炸前其内的气体压力和温度取为：p0=101.3 kPa，T0=293 K，准静态压力计算参数值：μH=2.67 m/s，αz=11.2，εc=6，βμ=1，KB=0.8，不考虑结构坍塌对于人员的伤亡影响.

3.1 泄爆面积影响分析

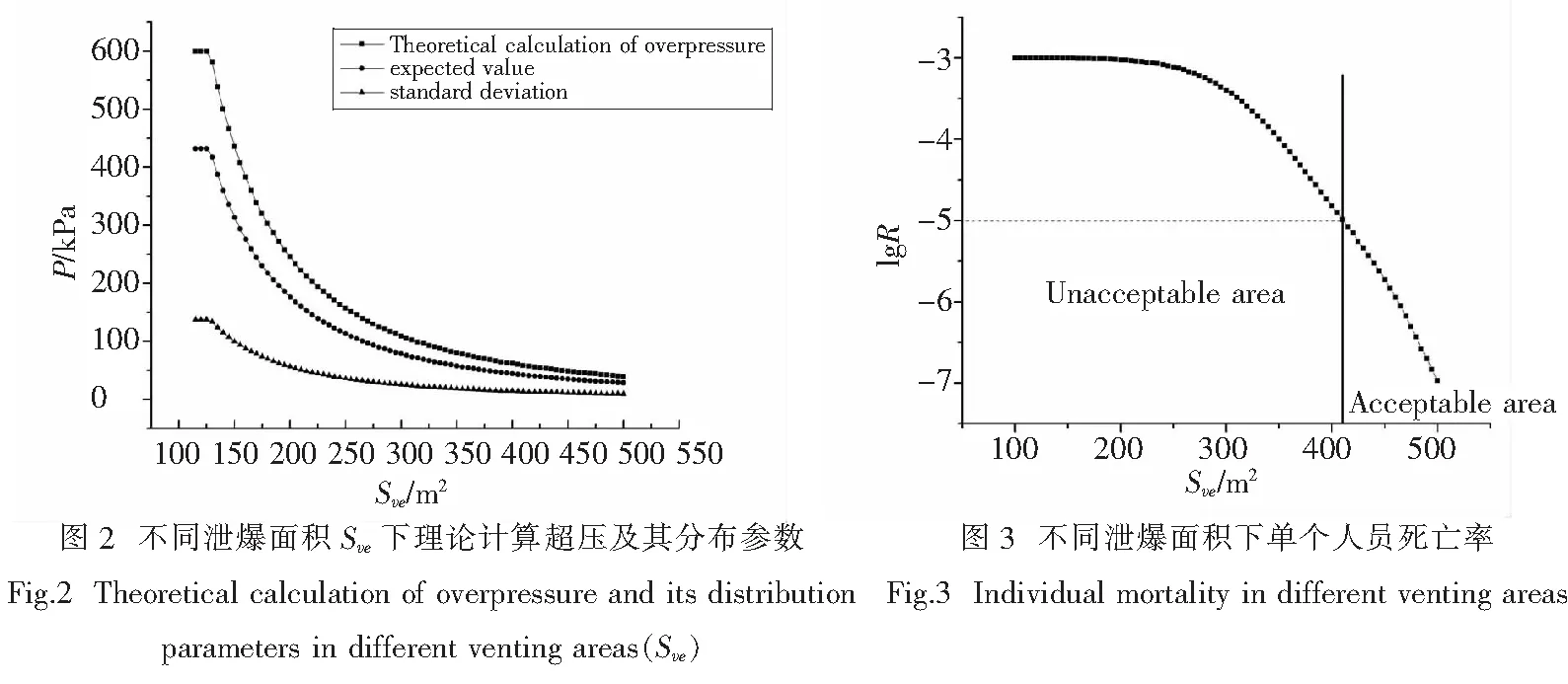
泄爆结构对应的破坏荷载特征值为：期望值μve=3.6 kPa，标准差σve=0.4 kPa.建筑物为危险性较大的有爆炸危险的工业厂房、仓库类，发生概率计算中K1取1%，K2取1，统计频率Pa取为1×10-5.根据风险接受标准，可接受人员死亡率为1×10-5.不考虑泄爆结构的打开时间，设计安全系数取1，利用式(8)～(10)，可计算得出不同泄爆面积Sve下理论计算超压及其分布参数，如图2所示.

结合图1中人员爆炸死亡概率，可得到不同泄爆面积下单个人员死亡率，如图3所示.当泄爆面积大于415 m2时，人员死亡概率小于1×10-5，处于可接受风险水平.利用美国消防协会NFPA68-2013、欧洲标准协会EN14994-2007以及中国国家标准GB50016-2014中的公式进行计算，可得到最小泄压面积分别为677 m2、420 m2、1 121 m2.计算结果表明，GB50016-2014标准中需要泄压面积最大，结果偏保守，NFPA68-2013标准计算结果与EN14994-2007相近，本文方法得到的泄压标准与其相符.

3.2 发生概率的影响分析

分析不同发生概率下不同泄爆面积对于单个人员死亡率的影响，如图4所示.发生概率取为10-5、10-4、10-3、10-2、10-1，随着发生概率不断增大，设计泄爆面积逐渐增大.当发生概率取为10-5时，人员死亡概率必然处于可接受水平，对于设计泄爆面积没有要求；当发生概率取为10-4、10-3、10-2、10-1时，对应的设计泄爆面积为355 m2、415 m2、465 m2、500 m2.从结果看，发生概率呈指数变化时，对于泄爆面积的影响不大，都小于GB50016—2014设计中的泄爆标准.

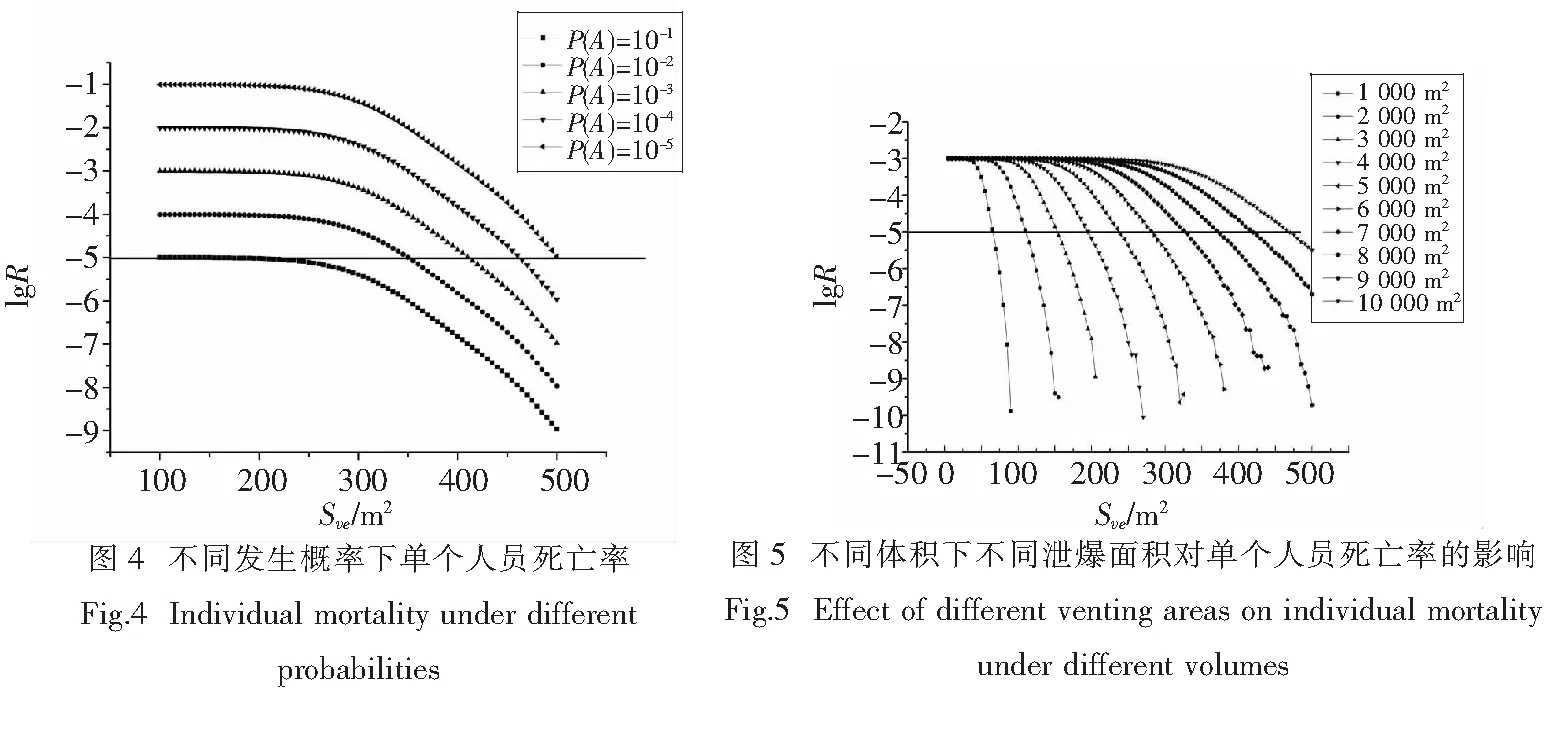
3.3 爆室体积的影响分析

在GB50016—2014标准、欧洲标准协会EN14994—2007中，爆室体积对泄爆面积的计算影响都很大，分析不同体积下不同泄爆面积对于单个人员死亡率的影响，如图5所示.当泄爆体积在1 000～10 000 m3时，对应的设计泄爆面积在70～470 m2之间，可以看出爆室体积对于设计泄爆面积的影响很大，与GB50016—2014计算结果之比在0.28～0.41之间.图6分析不同爆室体积下不同设计安全系数对于泄爆面积的影响，从图6可以看出，本文所采用的方法中，当安全系数取值在5～7时，设计泄爆面积与GB50016—2014设计中的泄爆标准保持一致.