关于高阶张量的秩-(Lr,1,1)分解方法

尹 凤, 雷晓军, 黄光鑫

(1.四川轻化工大学 数学与统计学院，四川 自贡643000；2.成都理工大学 信息与计算科学系，成都610059)

近年来，张量分解得到了越来越多的关注，取得了大量研究成果。在矩阵的奇异值分解(SVD)向张量分解的扩展过程中，Trucker分解或高阶奇异值分解(HOSVD)[1]和CANDECOMP/PARAFAC分解(简称为CP分解)[2-3]是2种主要的张量分解方法。这2种张量分解方法对应于2种不同的矩阵的秩。Trucker分解/HOSVD对应于矩阵的模-n秩，而CP分解与矩阵或张量的扩展所需的秩-1组件的最小数量对应。Trucker分解是一种高阶的主成分分析，其基本思想是：将一个张量分解为一个核心张量沿每一个模乘上一个矩阵；Trucker分解的优点是：可以用一个张量的大部分有用信息来表示原张量；不足之处是：Trucker分解的唯一性不能保证。CP分解的基本思想是：将一个张量表示成有限个秩-1张量之和。其优点是：能将张量进行降维处理；不足之处是：求CP分解的秩是一个NP问题，实际中只能通过低秩逼近等近似方法确定。

本文研究的高阶张量的秩-(Lr,1,1)分解方法受到了块组件分解[4]方法的启发，将高阶张量进行降维，即分解成一个矩阵与2个向量的组合，不同于其他张量分解方法。秩-(Lr,Lr,1)分解方法将张量分解成2个矩阵和一个向量的组合，秩-(L,M,N)分解方法将张量分解成3个矩阵的组合，秩-(L,M,·)分解方法则是将张量分解成2个矩阵的组合。本文在Trucker分解[1]和CP分解[2-3]的基础上，提出了一种高阶张量的秩-(Lr,1,1)分解，得到了一种交替最小二乘求解方法。

1 预备知识

本节是全文的基础。我们首先引入几个基本概念和符号，然后简要地介绍3种近年来发展的块分解方法，即秩-(Lr,Lr,1)分解、秩-(L,M,N)和秩-(L,M,·)分解。

1.1 基本概念和记号

R和C分别表示实数和复数域，有时我们也统一用K代替R或C。标量用小写字母a,b,…表示；向量用粗体小写字母a,b,…表示；矩阵用粗体大写字母A,B,…表示；张量用花体字母A，B,C,…表示。矩阵A中行标为i、列标为j的元素表示为aij=(A)ij，相应地，aijk=(A)ijk。令A=[a1a2…]，其中ai是矩阵A的第i列。定义矩阵A与B的克罗内克积为

(1)

设A=[A1A2…AR]，B=[B1B2…BR]是2个块矩阵，则矩阵A与B的Khatri-Rao内积[5]定义为

A⊙B=(A1⊗B1…AR⊗BR)

(2)

特别地，符号⊙c定义逐列的Khatri-Rao内积，即：A⊙cB=(a1⊗b1…aR⊗bR)。上标T和†分别定义为转置、复共轭转置、Moore-Penrose广义逆。一个矩阵A的向量化定义为vec(A)=[a1Ta2T…]T。符号δij代表克罗内克积函数，即当i=j时，δij=1；否则δij=0。

定义1令T∈KI1×I2×I3，A∈KJ1×I1，B∈KJ2×I2，C∈KJ3×I3则Trucker模-1乘积T·1A，模-2乘积T·2B，和模-3乘积T·3C分别定义为

(3)

(4)

(5)

定义2一个张量T∈KI×J×K的F范数定义为

(6)

定义3[6]给定2个具有相同维度的张量A和B，定义A与B的内积为

(A,B)=∑ijkaijkbijk

(7)

当A=B时，对应的张量范数是‖A‖=(A,A)1/2。

定义4张量A∈KI1×I2×…×IP和张量B∈KJ1×J2×…×JQ的外积A ∘B定义为

(A ∘B)i1i2…iPj1j2…jQ=ai1i2…iPbj1j2…jQ

(8)

定义5[7]一个张量T∈KI1×I2×I3的模-n向量是一个In维向量，通过变化指标in保持其他指标固定。其中In表示n阶单位矩阵。

定义6一个三阶张量是秩-(L,M,N)的，如果它的模-1秩、模-2秩和模-3秩分别是L，M和N。

一个秩-(1,1,1)张量简称为1-秩张量。此定义与下述是等价的。

定义7一个张量T的模-n秩是由它的模-n向量张成的子空间的维数。

定义8一个三阶张量T是1-秩的，如果它等于3个向量的外积。

张量的秩定义如下：

定义9[8]张量T的秩是由1-秩张量的所有线性组合中的1-秩张量的最小个数。

由定义9，我们定义一个三阶张量的标准矩阵或向量表示。

定义10[9]标准的JK×I矩阵表示(T )JK×I=(T)JK×I，KI×J表示(T )KI×J=(T)KI×J，IJ×K表示(T )IJ×K=(T)IJ×K，定义为

(TJK×I)(j-1)K+k,i=(T )ijk

(9)

(TKI×J)(k-1)I+i,j=(T )ijk

(10)

(TIJ×K)(i-1)J+j,k=(T )ijk

(11)

对所有角标的所有值。

张量T的标准的IJK×1向量记为TIJK=tIJK,定义为

(tIJK)(i-1)JK+(j-1)K+k=(T )ijk

(12)

对所有角标的所有值。

进一步地，张量T∈RI×J×K的第i个J×K矩阵切片记为TJ×K,i；类似地，第j个K×I切片和第k个I×J矩阵切片分别记为TK×I,j和TI×J,k。

1.2 块分解方法简介

1.2.1 秩-(Lr,Lr,1)分解

定义11[7]张量T∈RI×J×K分解成秩-(Lr,Lr,1)组件，是一种如下形式的分解

(13)

其中矩阵Ar∈KI×Lr和矩阵Br∈KJ×Lr是秩-Lr，1≤r≤R,cr为矩阵C的第r个列向量。称(13)式为张量T∈RI×J×K的秩-(Lr,Lr,1)分解。记A=[A1A2…AR],B=[B1B2…BR],C=[c1c2…cR]，用T的矩阵形式表示，(13)式可以写成

TIJ×K=[(A1⊙cB1)lL1… (AR⊙cBR)lLR]·CT

(14)

TJK×I=(B⊙C)·AT

(15)

TKI×J=(C⊙A)·BT

(16)

1.2.2 秩-(L,M,N)分解

定义12[7]张量T∈RI×J×K分解成秩-(L,M,N)组件，是一种如下形式的分解

(17)

其中Dr∈KL×M×N是秩-(L,M,N)，Ar∈KI×L(L≤I)，Br∈KJ×M(M≤J)，Cr∈KK×N(N≤K)是列满秩，1≤r≤R。称(17)为张量T∈RI×J×K的秩-(L,M,N)分解。记块矩阵A=[A1A2…AR]，B=[B1B2…BR]，C=[C1C2…CR]，用T的标准矩阵分解表示，(17)式可以写成

TJK×I=(B⊙C)·bdiag((D1)MN×L,…,(DR)MN×L)·AT

(18)

TKI×J=(C⊙A)·bdiag((D1)NL×M,…,(DR)NL×M)·BT

(19)

TIJ×K=(A⊙B)·bdiag((D1)LM×N,…,(DR)LM×N)·CT

(20)

其中bdiag(A1A2…An)，表示一个主对角块为A1A2…An的块对角矩阵。

对于张量T的IJK×1向量表示，此分解能写成

(21)

1.2.3 秩-(L,M,·)分解

定义13[7]张量T∈RI×J×K分解成秩-(L,M,·)组件，是一种如下形式的分解

(22)

其中：Cr∈KL×M×K,且Cr的模-1秩等于L，模-2秩等于M；Ar∈KI×L(I≥L)；Br∈KJ×M(J≥M)是列满秩，1≤r≤R。称(22)式为张量T∈RI×J×K的秩-(L,M,·)分解。记块矩阵A=[A1A2…AR]和B=[B1B2…BR]，用张量T的标准矩阵表示，(22)式可以写成

(23)

TJK×I=[(C1·2B1)JK×L… (CR·2BR)JK×L]AT

(24)

TKI×J=[(C1·1A1)KI×M… (CR·1AR)KI×M]BT

(25)

2 秩-(Lr,1,1)分解及其计算

2.1 (Lr,1,1) -秩分解及基本唯一性

定义14将张量T∈RI×J×K分解成秩-(Lr,1,1)组件(1≤r≤R)是一种如下形式的分解

(26)

我们称(26)式为张量T∈RI×J×K的秩-(Lr,1,1)分解。类似地，我们记A=[A1A2…AR]，B=[b1b2…bR]，C=[c1c2…cR]，则(26)式可以写成

TIJ×K=(A⊙B)·CT

(27)

TJK×I=(B⊙cC)·AT

(28)

TKI×J=(C⊙A)·BT

(29)

利用T的矩阵切片，(26)式能写成

TJ×K,i=B·bdiag{[(A1)i1… (A1)iL1]T, …,

[(AR)iR… (AR)iLR]T}·CT

(i=1,…,I)

(30)

TK×I,j=C·bdiag(bj1IL1×L1,…,bjRILR×LR)·AT

(j=1,…,J)

(31)

TI×J,k=A·bdiag(ck1IL1×L1,…,bkRILR×LR)·BT

(k=1,…,K)

(32)

注意：(26)式能任意前置不同的秩-(Lr,1,1)块，而且，只要它们的乘积保持不变，同一个秩-(Lr,1,1)组件的因子能够放缩。我们称这种分解是基本唯一的。图1给出了一个张量T∈RI×J×K的秩-(Lr,1,1)分解的示意图。

以下定理给出了张量T∈RI×J×K的秩-(Lr,1,1)分解的基本唯一性。

图1 张量的秩-(Lr,1,1)分解示意图Fig.1 Sketch showing the rank-(Lr,1,1) decomposition of a tensor

定理1令(A,B,C)表示T的秩-(Lr,1,1)分解，1≤r≤R, 假定A是列满秩，B和C没有成比例的列，那么(A,B,C)是基本唯一的。

证明假设c21, …,c2R不为0，并且c11/c21, …,c1R/c2R两两不相同，否则，考虑矩阵切片的线性组合。由(32)式，我们有

TI×J,1=A·bdiag(c11IL1×L1,…,c1RILR×LR)·BT

(33)

TI×J,2=A·bdiag(c21IL1×L1,…,c2RILR×LR)·BT

(34)

(A†·TI×J,2)T=B·bdiag(c21IL1×L1,…,c2RILR×LR)

(35)

矩阵C最后由(27)式可得

C=[(A⊙B)†TIJ×K]T

(36)

2.2 交替最小二乘算法

给定B和C，更新A是一个线性最小二乘问题。同样，当给定A和C时可以更新B；当给定A和B时可以更新C。详细的更新规则如下： 记A=[A1A2…AR],B=[b1b2…bR],C=[c1c2…cR]，则(26)式可以写成

TJK×I=(B⊙cC)·AT

(37)

TKI×J=(C⊙A)·BT

(38)

TIJ×K=(A⊙B)·CT

(39)

分别将(37)～(39)式进行简单地变换，我们可以得到算法1。

算法1给出了计算张量T∈RI×J×K的秩-(Lr,1,1)分解的交替最小二乘算法。注意，在实际计算中，矩阵B⊙cC,C⊙A和A⊙B必须具有至少与列一样多的行，并且必须是列满秩。如果A是列满秩，B和C没有成比例的向量，那么根据前面的证明过程，这个算法能通过广义特征值进行初始化，分解具有基本唯一性。

算法1交替最小二乘(ALS)算法计算秩-(Lr,1,1)分解

(1)初始化B,C,kmax

(2)fork=1,2,…,kmax直至收敛

①更新A:A←[(B⊙cC)†TJK×I]

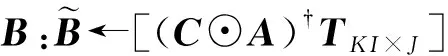
(3)endfor

(4)输出A、B和C。

3 数值实验

实例1

我们按照如下形式

(40)

图2 不同算法的相对误差与均方差之间的关系Fig.2 Relative error vs. negative logarithm of mean square variance of different methods

图3 不同算法的CPU时间与均方差之间的关系Fig.3 CPU time vs. negative logarithm of mean square variance of different methods

从图2可知，秩-(Lr,1,1)分解对应的算法1产生了最低的相对误差，效果最好。从图3可以看出，秩-(Lr,1,1)分解方法所需CPU时间最短。

实例2

图4 不同算法的相对误差与均方差之间的关系Fig.4 Relative error vs negative logarithm of mean square variance of different methods

图5 不同算法的CPU时间与均方差之间的关系Fig.5 CPU time vs negative logarithm of mean square variance of different methods

4 结 论

本文提出了一种新的张量块分解方法，即秩-(Lr,1,1)分解，并提出了求解张量的秩-(Lr,1,1)分解的交替最小二乘法算法。实验结果说明了本文所提出的秩-(Lr,1,1)分解方法的有效性。