列车通行条件下高速铁路人行天桥表面压力脉动研究

2019-01-24赵健业李小白梁习锋

铁道建筑 2019年1期

尹京，赵健业，李小白，梁习锋

(1.高速铁路轨道技术国家重点实验室，北京 100081；2.轨道交通安全教育部重点实验室，湖南长沙 410075；3.轨道交通安全关键技术国际合作联合实验室，湖南长沙 410075；4.轨道交通列车安全保障技术国家地方联合工程研究中心，湖南长沙 410075)

随着我国高速铁路技术的不断发展，列车运行时速呈现逐步上升的趋势，列车高速运行所带来的气动效应方面的危害日益显著[1]。当列车高速穿行于车站人行天桥底部正线时，桥体表面受到较大的瞬变气动荷载作用，引发桥体结构的振动并影响到桥上旅客的舒适性以及桥体结构的疲劳寿命。这一荷载与列车的车型以及速度有关，且与桥梁的自身结构密切相关。当列车在桥底交会时，由气动效应引发的桥体结构振动现象更加突出。因此有必要对列车穿行跨线天桥这一情况下的流场结构以及气动载荷加以研究，为铁路沿线跨线天桥的结构设计提供依据。

Yang等[2]通过实车试验以及数值仿真，研究了不同速度等级下列车单车通行时天桥表面的压力时程变化规律。Hur等[3]则通过风洞试验以及数值计算的方法研究了风荷载作用下列车车站的压力分布。Baker等[4]通过动模型试验研究了列车通行所引起的轨侧及轨顶设施表面压力脉动分布，并推导出气动荷载的相关公式。Zhou等[5]通过动模型试验研究了列车通过铁路车站时轨侧脉动压力对站台屏蔽门的影响，并总结了屏蔽门表面压力脉动沿列车运行方向的分布规律。已有研究针对列车通行于铁路车站的工况，主要给出了轨侧以及轨顶设施压力脉动沿列车运行方向或横向的分布特性，然而并未对天桥底面的脉动压力场分布给出合理描述。

本次研究通过数值仿真计算分析，针对国内某型高速动车组，计算单车以不同运行速度通过高速铁路人行天桥时天桥表面的气动荷载空间变化规律。

1 计算模型

1.1 几何模型及边界条件

列车模型如图1(a)所示。列车采用3车编组，忽略了受电弓等细微结构，采用较为简化的转向架结构。这一处理使得列车周围的流场不会受到太大的影响，同时易于网格划分，有利于数值计算的收敛。

图1 几何模型

桥梁模型如图1(b)所示。由于主要研究列车通行引起的桥梁结构表面的压力波动，因此忽略对这一物理效应影响较小的其他环境因素。站房设施以及顶部雨棚等距离模型区域较远的结构未予考虑。桥梁模型保留了距离模型区域较近的设施如电梯以及桥底梁结构，但是较细微的结构由于其加大了网格划分难度，未予考虑。

单车通行时的计算区域见图2。桥体、地面以及车身均采用无滑移壁面；两侧以及顶部边界采用对称平面边界条件；列车行驶正前方的边界设置为静压为0的压力出口边界；其正后方则采用压力入口边界。

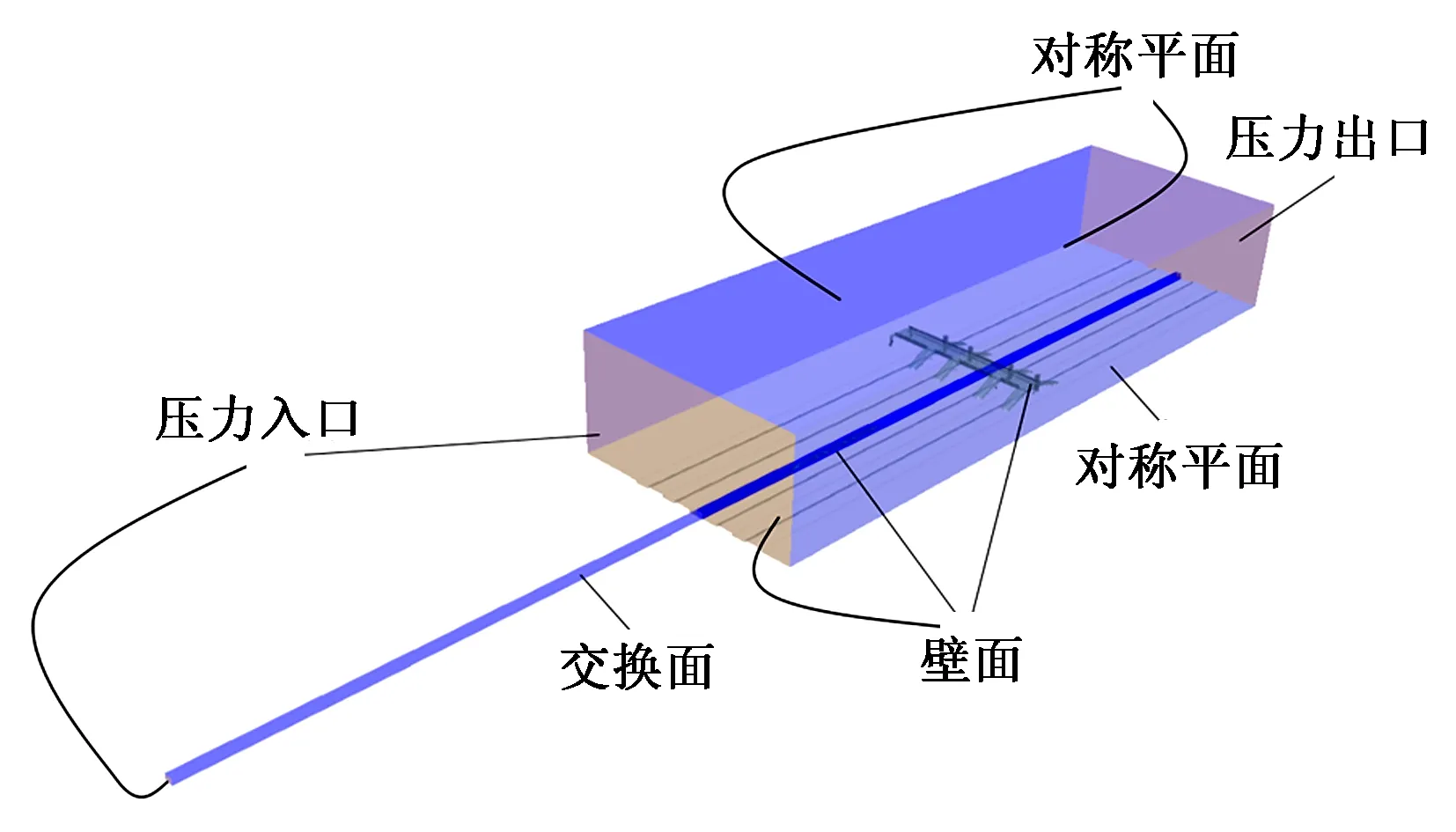
图2 单车通行时的计算区域

为了模拟列车与大计算域之间的相对运动，列车车身设置小滑移域并给定与行驶速度相同的滑移速度(250,300,350,400 km/h)，通过交换边界与大域进行数据交换[6-7]。

为了使得边界条件上的数值不影响模型区域的计算结果，侧面、前后以及顶部边界均应与模型区域有足够的距离。计算域长度为500 m，高度为80 m，宽度为160 m，桥梁模型放置在计算域正中央。为了使列车在到达天桥区域时流场处于合理状态，列车初始位置距离桥底中心100 m。小域长度的选取准则是确保列车滑移过程中前后方出口始终不得进入到大域内部。坐标原点位于桥梁中心线底部单车正线处，z=0对应地面高度，x方向指向列车运行方向，y方向与桥梁中心线平行。

1.2 网格划分

采用四面体有限体积单元对计算区域进行网格划分。在头尾车等曲率较大处以及转向架等结构细小处进行局部网格加密，以充分还原几何特征并捕捉细微流场结构。

桥体表面同样在结构细微处进行网格加密。表面网格的划分保证所研究区域的局部n+值处在30～100之内。此外，为了充分捕捉所研究区域的流动状态，在车身周围以及桥底以及正线之间的空间区域采用局部体网格加密。由于远离车身部位的流动不足以影响到列车周围的流动，因此该部位的网格尺度较大,网格数量约1 300万。

1.3 求解设置

1.4 测点布置

在桥梁底面以及迎风侧表面均布置了压力测点。图3(a)所示为天桥底面测点，纵向L1—L7为测线，横向1～9表示各测线上相应测点序号。L1,L7对应到发线;L3,L5对应正线;L2和L6对应桥底x方向梁的位置;L4位于2条正线中心。L1—L7测线对应的y坐标分别为6.5,3.6,0,-2.5,-5.0,-7.4,-11.5 m。测点1～9对应桥底纵梁位置以及梁之间空腔的中点，其x坐标分别为-6.00,-4.31,-3.00,-1.50,0,1.50,3.00,4.31，6.00 m。1,9号测点高度为7.74 m。L2和L6的2～8号测点高度为8.60 m；对于其他测线梁处测点高8.68 m，空腔内测点高9.07 m。

图3(b)所示为迎风面测点。L1—L7定义与上述一致。1～4号测点则对应不同高度，1号测点位于桥底支撑梁迎风面，2～4号则位于挡风屏障。1号测点x坐标为-6.53 m，z坐标为8.43 m；2～4号测点x坐标为-7.50 m，z分坐标别为9.92,10.42，10.92 m。

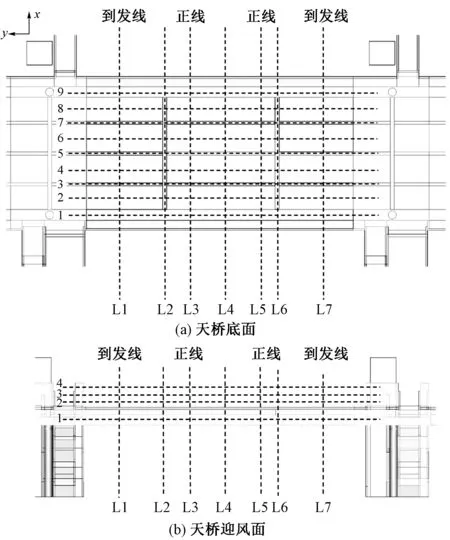
图3 测线及测点布置

2 计算结果与分析

2.1 气动效应分析

已有研究表明，对于线路侧典型测点，其压力在列车头部到达测点的前一段时间开始缓慢增加，在列车头部鼻尖到达测点时迅速增大，产生一正、负脉冲，即头波；在最大负脉冲出现后开始等幅波动，直到尾车鼻尖通过测点时，产生一负、正脉冲，即尾波；再等幅波动直到会车结束后一段时间，信号才逐渐消失[1-2]。

单车通行情况下，头车经过桥底的过程中天桥底面的压力云图如图4(a)所示。可见，天桥底面压力时程变化是受列车运行时车身周围空气压力的影响。当列车鼻尖靠近时桥体底面压力逐渐升高，并在鼻尖到达测点时压力达到最大。随后由于头车流线形区域周围流速大负压高，桥体底面测点压力到达正峰值后立即下降并达到负峰值。瞬变压力的时间跨度是头部流线形长度与列车运行速度之比。在列车头部完全经过桥底后，桥底表面受到稳定的负压。当尾车通过时，天桥底面的压力变化过程与头车相反。尾车流线形部分通过时天桥底面受到较大的负压，随后压力开始迅速上升并在鼻尖到达时达到最大，之后压力开始下降，由于尾流的作用压力呈现等幅波动并逐渐变为0，如图4(b)所示。

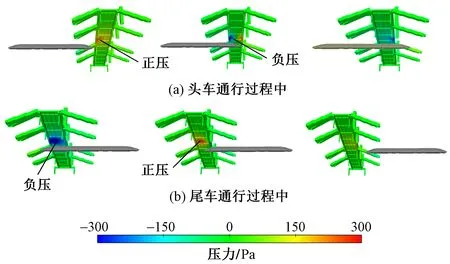
图4 天桥底面压力变化云图

2.2 雷诺数的影响分析

为了方便比较，对各个工况中各测点压力进行无量纲化处理。对所求解得到的压力值进行无量纲化，得到压力系数Cp，表达式为

CP=P/(0.5ρU2)

(1)

式中：P为数值求解得到的天桥表面压力；ρ为大气密度，取1.225 kg /m3；U为列车运行速度,m/s。

对时间无量纲化，即

t*=t/(H/U)

(2)

式中：t为从列车开始运行起计时的时间;H为参考高度，取值为车高3.95 m。

当列车的运行速度变化时，其对于周边流场的影响反映了流场雷诺数的影响。雷诺数的定义为Re=HU/ν，其中ν是空气的动力黏度。雷诺数的本质是流场中惯性效应与黏性效应的比值。当雷诺数较小时黏性力所占的比重较大，CP随雷诺数的变化较大。随着雷诺数的升高惯性效应所占的比重增加，黏性效应所占的比重减小，当雷诺数达到某一临界值时，CP基本上不随雷诺数的变化而产生较大的变化，这一临界值也被称为临界雷诺数。在列车空气动力学的研究中，临界雷诺数被广泛认为是2.5×105，当然对于不同的工况该值可能会发生变化。

天桥底面L1上各测点头波压力变化峰峰值与列车速度的关系见图5。当列车速度变化导致相应的流场雷诺数改变时，计算所得到的压力变化峰峰值变化较小。与400 km/h工况头波压力变化峰峰值相对偏差最大的点出现在P2，但是依然未超过0.8%。因此从压力变化峰峰值的角度而言，可以认为在本次计算的雷诺数条件下流场已经达到自模拟状态，故下文以400 km /h 的工况为例进行分析。

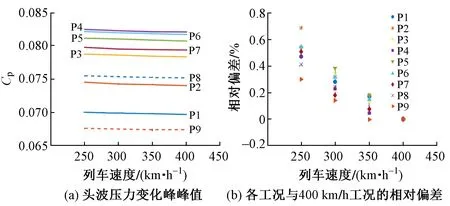
图5 压力变化峰峰值与列车速度的关系

2.3 压力测点脉动值分析

列车单车通行条件下，天桥底面L3测线上测点的压力变化时程曲线见图6，天桥迎风侧L3测线上测点的压力变化时程曲线见图7。可见，桥底面同一测线上的测点由于在沿列车行进方向位置不一，因此测点处压力达到正峰值的时间存在先后差异，且靠近桥底中心的测点压力变化峰峰值更大，边缘的测点更小。对于迎风侧的测点高度越低压力变化峰峰值越大。

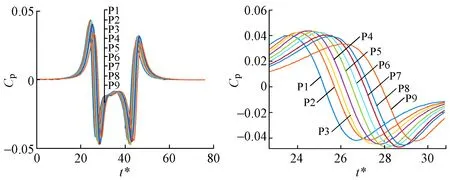
图6 列车单车通过时天桥底面L3测线上测点压力时程曲线(右图为局部放大图)

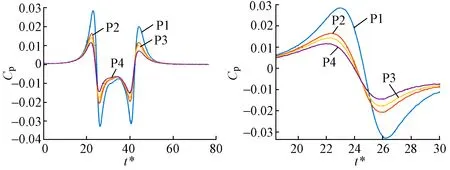
图7 列车单车通过时天桥迎风侧L3测线上测点压力变化时程曲线(右图为局部放大图)

列车单车通行条件下，天桥底部各测线P5测点的压力变化时程曲线见图8，天桥迎风侧各测线P2测点压力变化时程曲线见图9。

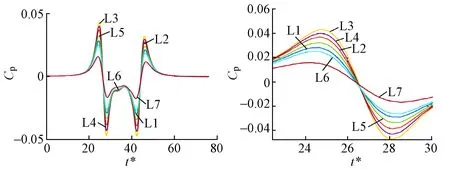
图8 列车单车通过时天桥底面各测线P5测点压力变化时程曲线(右图为局部放大图)

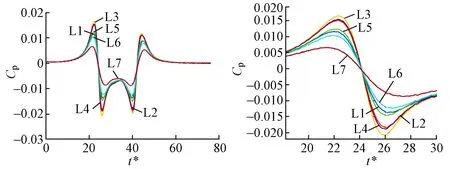
图9 列车单车通过时天桥迎风侧各测线P2测点压力时程曲线(右图为局部放大图)

由图8、图9可见:由于测点距列车中心线的位置不同，因此其压力变化存在差异。对于桥底面以及迎风侧的测点，距离列车中心线越近压力变化峰峰值越大，这一规律与文献[2]的研究结果一致。

天桥底面、迎风侧各测点处的头波压力变化峰峰值分别见表1、表2。

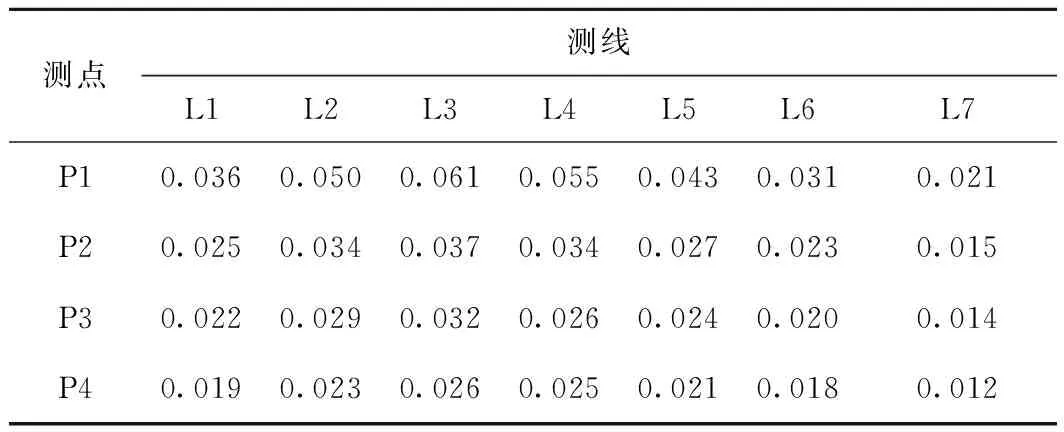
表2 天桥迎风侧测点头波压力变化峰峰值CP

列车单车通过条件下，天桥各测点头波压力变化峰峰值分布见图10。可见：头波压力变化峰峰值最大值出现在天桥底部对应于列车运行正线位置的L3的中心P5测点，其值为0.09。对于底面测点而言，距离正线越近压力变化峰峰值越大；同一条测线上的测点距离桥底部中心线越近压力变化峰峰值越大。对于迎风侧的测点而言，所有测线上的1号测点压力变化峰峰值显著高于其他测点；随着测点高度的增加，压力变化峰峰值逐渐减小；且同样存在正线位置处压力变化峰峰值最大的趋势。