一种用于卷积神经网络压缩的混合剪枝方法
2019-01-24靳丽蕾杨文柱王思乐崔振超陈向阳陈丽萍
靳丽蕾,杨文柱,王思乐,崔振超,陈向阳,陈丽萍
(河北大学 网络空间安全与计算机学院,河北 保定 071002)
1 引 言
近几年,卷积神经网络(Convolutional Neural Network,CNN)作为深度学习中的经典模型,在图像分类、目标检测和语义分割等诸多领域取得了一系列的研究成果.自2012年深度学习算法在识别精度方面表现出巨大优势后,各种深度学习模型便相继涌现.但是这些模型在不断逼近计算机视觉任务精度极限的同时,其模型深度和参数也在成倍增长,使得这些模型很难应用于资源受限的设备.由表1[1-4]可以看出,CNN的层数越来越多,使得其计算复杂度越来越高,而过高的计算复杂度要使用GPU或者更高性能的CPU实现神经网络运算.由于手机等移动设备、车载嵌入式设备等存在计算能力、存储容量等诸多方面的约束,现有的深度神经网络无法在这些资源受限设备上进行很好的部署使用.目前模型压缩的关键就是如何在保持现有神经网络性能基本不变的情况下,通过减小网络的计算量和网络模型存储,使其能在资源受限的设备上高效运行.因此,模型压缩与加速受到学术界和工业界的极大关注,其中合理有效地修剪冗余参数最具挑战性.
自AlexNet[1]在2012 ILSVRC上取得突破性成果后,越来越多的研究人员开始研究CNN模型.最具代表性的CNN模型,如VGG[2],GoogLeNet[3],ResNet[4]和DenseNet[5],大大提高了模型精度.其中,VGG网络的卷积层占据了大约 90-95% 的计算时间和参数规模;全连接(FC)层占据了大约 5-10% 的计算时间和95% 的参数量,这为研究深度模型的压缩提供了统计依据.深度神经网络在各种计算机视觉任务中(比如遥感图像的分类[6])都非常有效,但由于参数过多难以部署在手机等资源受限的设备上.
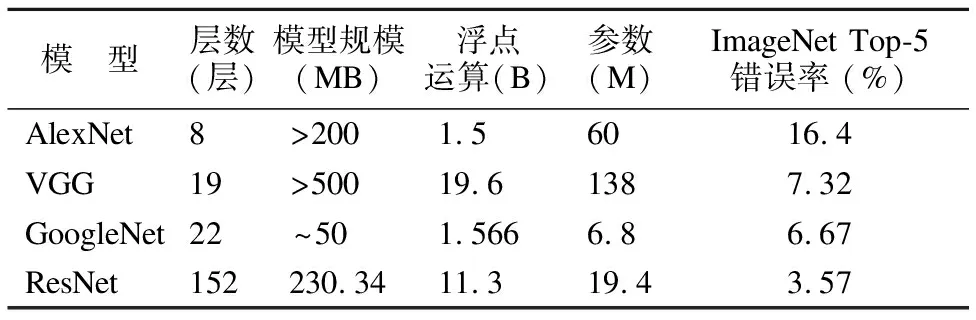
表1 几种经典卷积神经网络模型的对比Table 1 Comparison between some CNN models
剪枝是用于降低网络复杂度、加速网络模型的有效方法,可以在几乎不损失模型精度的前提下移除网络中的冗余参数,达到模型压缩的目的.20世纪90年代,LeCun等人[7]便提出了Optimal Brain Damage方法对模型进行剪枝,有效降低了网络复杂性并缓解了过拟合问题.神经网络中包含很多参数,但有些参数对最终输出的贡献很小,可以认为这些参数是冗余的.因此,需要找到有效的评估方法,对不重要的参数进行剪枝以减少模型参数冗余.Han等人[8]提出了一种简单的剪枝方法,不会损失准确性;其主要思想是移除权重低于指定阈值的所有连接.虽然这个方法稀疏度很高,但在实际加速中其效果有限.卷积核剪枝可以解决该方法的局限性,有效实现模型压缩与加速.但在模型压缩时,单独使用权重剪枝或卷积核剪枝得到的网络仍然存在参数冗余.本文提出了一种结合权重剪枝和卷积核剪枝的混合剪枝方法,以实现最大限度的模型压缩.
2 相关工作
为了提升网络的性能,深度卷积神经网络在增加深度的同时,极大增加了参数量.Denil等人[9]证明了卷积神经网络可以用它原始参数的一个子集进行有效的重建,表明网络中存在参数冗余问题.目前有很多不同的模型压缩与加速方法,大致可以分为五类:新型网络模块设计、知识蒸馏、低秩分解、量化、剪枝.
关于新型网络模块设计的研究有很多,比如SqueezeNet[10],MobileNet[11]和ShuffleNet[12].基于更细致更高效的原则设计新型网络模型有效减小模型尺寸且有良好的性能,但设计新的网络结构对技巧和经验要求较高.Lei等人[13]基于知识迁移[14]提出了知识蒸馏(Knowledge Distillation,KD)方法,该方法在保持一定性能的前提下将深层网络压缩成较浅的网络,有效降低了计算量;但它只能用于具有SoftMax 损失函数的分类任务,且模型假设有时过于严格,导致在性能方面无法与其它方法竞争.权重矩阵分解利用网络中计算单元的矩阵来实现信息重组,达到网络压缩的目的.网络模型中,每层的权重都可以通过该层的权重子集进行精确预测,可使用奇异值分解(SVD)[15]来对每一层进行低秩近似.然而,低秩分解技术已经很成熟,并且现在越来越多网络中采用诸如1×1、3×3这样的小卷积核,而对这些小卷积核用矩阵分解的方法很难实现网络加速和压缩;另外,目前的分解方法都是逐层执行低秩近似,无法执行全局参数压缩.嵌入式处理器由于位宽和性能的限制,导致常规的计算需求在该环境下难以得到满足.面对这种情况,在保证网络模型精度的同时对网络中的权重数据使用量化方法已成为一种趋势,但由于实现难度大、准确性不稳定等问题导致量化方法使用门槛较高.
剪枝方法被广泛应用于压缩CNN模型.Srinivas等人[16]研究了神经元之间的冗余问题,并提出了一种无数据剪枝方法.Chen等人[17]提出了一个HashedNets模型,使用低成本的散列函数将权重分组为哈希表进行参数共享.Han等人[18]提出了“Deep Compression”方法,主要包括参数剪枝、量化和霍夫曼编码.Ullrich等人[19]提出了一种基于软权重共享的简单正则化方法.韩等人[20]提出了网络删减、参数共享相结合的压缩方案.对于已经训练好的模型,可以找到一种有效的评估方法,对不重要的卷积核进行剪枝以减少模型冗余,这是目前模型压缩中使用最多的方法.Li等人[21]基于权重的大小提出了一种简单的剪枝方法来衡量每个卷积核的重要性,对每个卷积核中所有权重的绝对值求和作为该卷积核的评价指标.Hu等人[22]定义零的平均百分比APoZ(Average Percentage of Zeros)来衡量每一个卷积核中激活函数值为零的数量,作为评价卷积核重要与否的标准.这两个标准简单明了,但与最终损失没有直接关系.因此,Molchanov等人[23]采用泰勒展开式来近似的计算移除每个卷积核对损失函数的影响程度.Luo等人[24]认为难以通过权重大小判定每个卷积核的重要性,提出了基于熵的剪枝方法.Luo等人[25]在基于熵的剪枝方法基础上进行改进,设计出了效果更优的 ThiNet框架.该框架利用下一层的统计信息指导当前层的剪枝,在不改变原网络结构的前提下实现模型的加速与压缩.
基于模型剪枝的方法很多,其主要思想都是挑选出模型中不重要的权重或卷积核将其移除.移除不重要的权重或卷积核后,通过再训练来恢复模型的性能,这样就可以在保证模型性能的前提下,最大程度的压缩模型参数,实现模型加速.该类方法中,如何找到一个有效衡量权重或卷积核重要性的标准是关键问题.
3 CNN混合剪枝方法
对CNN进行剪枝能够有效降低它的参数量和运行需要的计算开销,解决CNN模型难以应用于资源受限设备的问题.对于权重剪枝,去掉低于阈值的权重连接,通过再训练恢复模型精度,最后可以得到一个稀疏模型.卷积核剪枝可以保持原始的网络模型不被改变,也不需要额外的深度学习库支持.为了得到更好的压缩效果,综合考虑卷积核剪枝与权重剪枝两种方法,提出了混合剪枝方法.
3.1 CNN混合剪枝的框架
给定一个原始网络,首先删除重要性低的卷积核来进行卷积核剪枝;然后,使用权重剪枝实现进一步压缩.与原始CNN相比,剪枝后的CNN具有更少的卷积核和权重.混合剪枝的框架如图1所示.
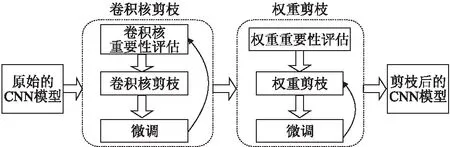
图1 网络混合剪枝的框架图Fig.1 Framework of mixed network pruning
3.2 卷积核剪枝
卷积核剪枝包括以下四个步骤:
1)评估卷积核的重要性.主要思想是使用i+1层的统计信息来指导i层的剪枝,使用i+1层输入的子集近似i+1层的输出.
2)剪除不重要的通道及其相对应的卷积核.i+1层输入中的通道由i层中的卷积核产生,因此可把i+1层不重要的通道和相应i层的卷积核安全地移除.
3)剪枝后会损坏模型的泛化能力,将整个网络微调一遍或两遍恢复其性能.
4)最后,判断剪枝是否结束.如果剪枝停止,可微调多次获得更准确的模型.否则,重复步骤(1)-(3)继续对下一层进行剪枝.
针对网络模型的第i+1层进行压缩,使用第i+1层的输入,即第i层的输出来模拟其输出的线性过程.如果通过优化的方法可以找到对于第i+1层的输入中线性组合等于零的部分,并将相应的第i层输出的卷积核舍弃掉,就可以利用较少的输入得到相似的输出,即在尽量不影响模型效果的前提下实现压缩模型.寻找线性组合的值接近于零的具体过程包括收集训练样本、用于通道选择的贪心算法、最小化重构误差等优化方法.
3.2.1 收集训练集
收集训练集以评估通道的重要性,确定通道是否可以安全地移除.由y表示的元素从i+2层中随机采样.i+1层中的相应卷积核和滑动窗口也可以根据其位置来确定.
卷积运算如下式:
(1)
进一步定义如下公式:
(2)
然后,公式(1)卷积操作可以简化为:
(3)
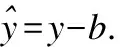
(4)
3.2.2 通道选择
卷积核剪枝的关键是衡量卷积核的重要性,常用的方法包括:通过卷积结果的稀疏程度、卷积核对损失函数的影响、卷积结果对下一层结果的影响等.训练之后,移除一些不重要的卷积核,然后每一层剪枝后微调一遍或两遍,以便恢复模型精度.

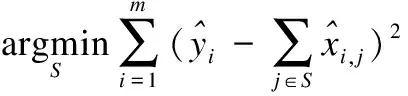
(5)
其中,|S|是子集S中元素的数量,r是预定义的压缩率.等价的,T表示被移除通道的子集,即S∪T={1,2,…,C} andS∩T=φ,就可以最小化下面的公式6来替代公式5:
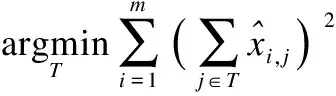
(6)
公式(6)等价于公式(5),但|T|的个数通常是小于|S|的,因此公式(6)比公式(5)更快更简单.解决公式(6)仍然是NP难题,可以使用如算法1所示的贪心算法来解决.假设T表示已移除通道的子集,其初始值为空集.U是所有通道的集合,对于每个i∈U,通过公式6计算值,每次选择添加一个通道使得通过当前样本得到的误差最小,最后获得移除通道的子集.这种方法是局部最优的,可通过微调来弥补这种方法造成的影响.
算法1. 贪心算法
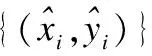
输出:移除通道的子集T
1.T←φ;U←{1,2,…,C};
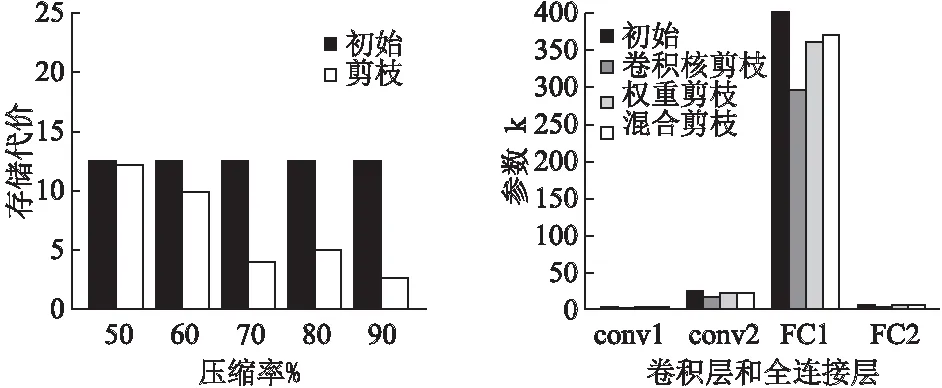
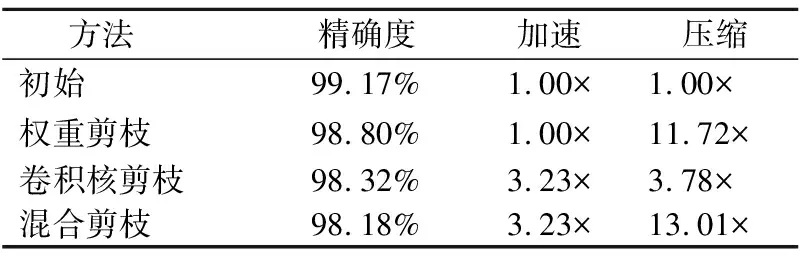
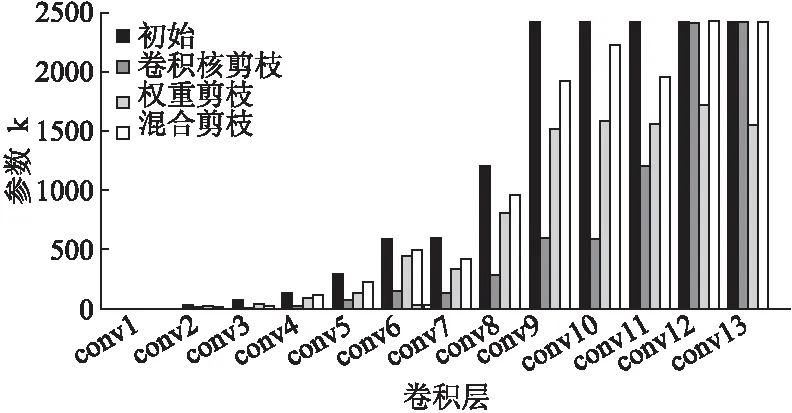
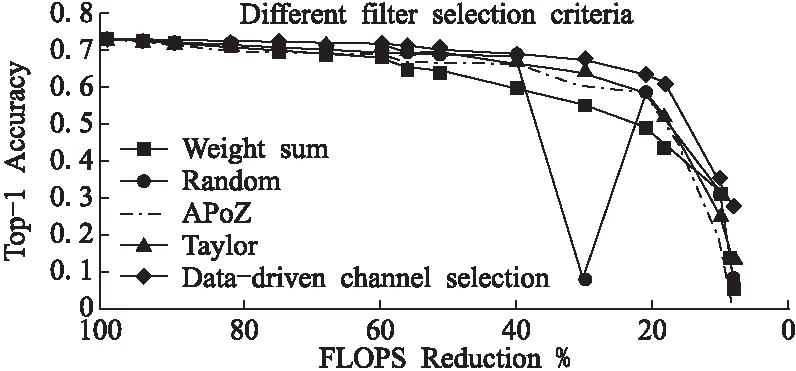
2.while |T| 3.min_value←+∞; 4. for each itemi∈Udo 5.tmpT←T∪{i}; 6. computevaluefrom Eq.(6)usingtmpT; 7. ifvalue 8.min_value←value;min_i←i; 9. end if 10. end for 11. movemin_ifromIintoT; 12.end while 3.2.3 最小化重构误差 在确定要保留哪些卷积核之后,通过通道的加权来进一步减少重构误差: (7) 权重剪枝包括3个步骤: 1)评估权重的重要性.正常训练得出的权重被视为相对重要和不重要的权重. 2)设置一个阈值,将小于阈值的权重设置为零,此时网络变为稀疏连接的网络. 3)重新训练这个稀疏网络以获得最终结果. 因数据量有限、训练参数多并且训练过度,卷积神经网络面临过拟合的问题,目前正则化和dropout是防止过拟合常用的两种方法.正常训练网络后,得到相对重要和不重要的权重;在权重剪枝时,L1/L2正则化方法、卷积层和全连接层会具有不同的敏感度. 3.3.1 正则化 通过增加深度,网络可以更好地近似损失函数,增加非线性,获得更好的特征表示.然而增加深度,网络的复杂性也会增加,使得网络难以优化并且更易过拟合.使用L1 / L2正则化和dropout等生成稀疏权重的方法来训练大而密的网络,然后删除网络中贡献较小的权重,即删掉一些冗余连接.另外,防止过拟合的最直接方法是增加使用的数据集和缩小使用的网络结构.但是,扩大数据集并不简单.减少网络结构固然可以有效减少参数数量,但一般网络越深,表达能力越强.因此,正则化和dropout的使用旨在解决过拟合的问题. L2 正则化是最常用的正则化方法,可表示为: (8) 其中C是正则化后的损失函数,C0是原始的损失函数.λ表示正则化因子.所以常用的交叉熵损失函数可以表示为: (9) 其中x代表样本,n代表样本总数,y是实际值,a是输出值.由上面的公式,正则化是通过在损失函数中加入权重惩罚因子来增加损失值以减小权重.使用正则化因子调整正则化:λ越大,越倾向于减小权重;λ越小,越倾向于减小原始的损失函数.在剪枝过程的第一次训练中,确定权重的重要与否.正则化程度将影响权重的大小,从而影响网络中的哪些连接需要进行剪枝. 与L2正则化不同,dropout通过改变网络结构解决过拟合的问题.在训练期间,dropout以一定概率将某些权重随机置为零,通过设置随机剪枝的概率,以增加网络稀疏性加速收敛,可按公式(10)(11)计算: Ci=NiNi-1 (10) (11) 其中Ci表示第i层的连接数,Ni表示第i层的神经元数目,Cio表示原来的连接数,Cir表示再训练时的连接数,Do表示原始的 dropout. 3.3.2 敏感度 不同的正则化方法和不同类型的层在剪枝时具有的敏感度不同,因此它们的剪枝阈值对精确度也会有不同的影响.逐层对神经网络进行灵敏度分析,将权重置为零后对神经网络精度影响很小的部分.然后对权重进行排序并设置一个阈值,将低于阈值的权重重置为零,保持这些权重不变,继续训练直到模型精度恢复,最后重复上述过程,通过增加阈值来增加模型中零的比例. 实验采用两种数据集,MNIST[26]手写数字识别和用于物体识别的CIFAR-10[27].CNN架构使用经典的LeNet-5和VGG-16.MNIST数据集有60,000个训练集和10,000个测试集.CIFAR-10由10类60,000个32×32彩色图像组成,每个类别有6000个图像.有50,000个训练图像和10,000个测试图像.分别与原始网络,权重剪枝和卷积核剪枝结果进行对比,验证混合剪枝方法的有效性.然后,将混合剪枝结果与现有方法(如APoZ,Weight sum和Taylor)进行比较.本实验在PyTorch[28]环境下进行. 实验中使用LeNet-5网络,它有两个卷积层,两个下采样层,两个FC层和一个分类层,在MNIST数据集上的错误率为0.8%.在MNIST数据集上进行剪枝和训练CNN.混合网络剪枝与三个基准比较: 1)原始模型:正常训练一个小的CNN不进行剪枝. 2)权重剪枝:移除权重低于阈值的所有连接. 3)卷积核剪枝:移除重要性低的卷积核. 使用LeNet-5网络在MNIST数据集上评估权重剪枝方法的性能.对于网络中低于阈值的所有权重进行剪枝获得压缩模型.如图2所示,将LeNet-5上的存储开销与不同的压缩比进行比较.在90%的压缩率下最大的降低存储代价,精度仅下降0.18%. 使用LeNet-5网络在MNIST数据集上评估卷积核剪枝方法的性能.从收集用于通道选择的训练集开始,从训练集中的每个类别中随机选择10个图像构成评估集.并且对于每个输入图像,用不同的通道和不同的空间位置随机采样10个实例.因此,总共有1000个训练样本用于通过贪心算法找到最佳通道子集.实验证明了这种选择的有效性(每个类10个图像,每个图像10个位置),足以进行神经元重要性评估.每层剪枝后微调一遍.当所有层都被修剪完,微调10遍以获得更高的准确度. 图2 不同压缩率下存储代价的比较Fig.2 Storage overhead comparison of different compression rate图3 LeNet-5在MNIST上参数减少的统计数据Fig.3 Parameters reduction statistics for LeNet-5 on MNIST 使用LeNet-5网络在MNIST数据集上评估混合剪枝方法的性能.卷积核剪枝的主要优点是该方法能直接影响网络结构的大小,删除对最后结果贡献不大的卷积核得到的网络可实现一定程度的压缩.对剪枝后的模型,再进行权重剪枝实现进一步压缩.如图3所示,LeNet-5在MNIST上通过不同剪枝方法得到每层参数数量的对比.FC层可用全局平均池化层(global average pooling,GAP)替换,但MNIST数据集和LeNet-5网络比较简单,因此本实验中保留了FC层.针对LeNet-5网络剪枝,主要对conv2和FC1中的权重和卷积核进行剪枝操作.实验结果表明,与仅进行权重剪枝或卷积核剪枝相比,所提出的混合网络剪枝方法可以显著减少参数的数量. 表2 剪枝前后LeNet-5模型的性能变化Table 2 Performance changes of the LeNet-5 model before/after pruning 如表2所示,剪枝前后的LeNet-5模型的性能变化.对于LeNet-5模型,使用权重剪枝虽然可以实现较好的压缩效果,但是没有加速效果.使用卷积核剪枝,可以实现压缩与加速,但是压缩效果与权重剪枝相比效果略差.而使用所提出的混合剪枝方法可以实现13.01×压缩和3.23×加速. VGG-16是一个16层的CNN,有13个卷积层和3个FC层,在CIFAR-10数据集上进行剪枝和训练CNN.与4.1节类似,提出的混合剪枝方法与三种基准在cifar10数据集上进行对比实验. 使用VGG-16网络在cifar10数据集上评估权重剪枝的性能.创建和VGG-16相同的架构,但将掩码和阈值变量添加到需要进行剪枝的层.变量掩码与网络层的权重张量具有相同的形状,确定哪些权重参与图的正向执行.然后,将操作添加到训练图中,该图监视层中权重大小的分布并确定层阈值,掩盖低于该阈值的所有权重,达到当前训练步骤所需的稀疏度水平. 表3 剪枝前后VGG-16模型的性能变化Table 3 Performance changes of the VGG-16 model before/after pruning 使用VGG-16网络在CIFAR-10数据集上评估卷积核剪枝方法的性能.CIFAR-10数据集包含从10个类别中抽取的50,000个训练图像.收集用于通道选择的训练集,然后从训练集中的每个类别中随机选择10个图像以构成我们的评估集.总共有1000个训练集用于通过贪婪算法找到最优通道子集.微调期间,网络每修剪一层后微调一遍.当所有层都被剪枝后,微调15遍以恢复准确性. 图4 VGG-16在Cifar10上每层参数减少统计Fig.4 Parameters reduction statistics for VGG-16 on Cifar10 使用VGG-16网络在cifar10数据集上评估混合剪枝方法的性能.首先移除不重要的卷积核,再对剪枝后的模型进行权重剪枝实现进一步的压缩.如图4所示,VGG-16在Cifar10数据集上通过不同剪枝方法得到每层参数剪枝数量的对比.结果表明,与仅使用权重剪枝或卷积核剪枝相比,所提出的混合剪枝方法显著减少了参数的数量.VGG-16网络的卷积层占有约90%的浮点运算,而FC层有89.36%的参数.出于模型加速的考虑,使用GAP层替换FC层会更简单有效.剪枝前后的VGG-16模型的性能变化如表3所示.与其它基准相比,混合剪枝方法可以实现更好的压缩与加速.对于VGG-16模型,使用所提出的混合剪枝方法可以实现19.20×压缩和3.31×加速. 针对不同的卷积核选择方法,在Dogs vs.Cats Kaggle数据集上对其性能进行实验评估,该数据集包含25000张狗和猫的图像.出于加速的考虑,使用GAP层替换FC层.因此,VGG-16中的所有FC层都将被删除并在新数据集上进行微调.然后,在获得该微调模型之后,以不同的压缩率逐层对网络剪枝.每一层剪枝之后微调一遍,最后一层剪枝完微调15遍以提高准确性,使用不同的卷积核选择策略重复该过程若干次.除了卷积核选择标准外,其它所有设置均保持不变.在Dogs vs.Cats Kaggle数据集上针对不同卷积核选择标准的剪枝结果,如图5所示. 图5 不同卷积核选择标准的性能比较Fig.5 Performance comparison of different filter selection criteria 与其他选择方法相比,Data-driven通道的选择标准几乎在整个剪枝比的范围内性能最优.与Data-driven的通道选择标准相比,泰勒标准性能稍差.Random选择标准表现出相当好的性能.但是,这个标准鲁棒性不好,并且在压缩所有层之后精度非常低,在实践中并不适用.Weight sum标准由于它只考虑权重的大小,具有相当差的精度.实际上,去除大量小的卷积核也会对精度产生很大影响. 表4 在VGG-16上与现有方法的比较Table 4 Comparison with existing methods on VGG-16 将所提出的方法与几种现有剪枝方法进行比较,结果如表4所示.APoZ旨在减少参数数量,但其性能有限.相反,Taylor旨在模型加速,并且只对卷积层进行剪枝.但计算过程可能非常耗时,因此他们使用Taylor展开来近似剪枝的优化问题.我们在Data-driven的通道选择方法基础上进行权重剪枝,最后得到的结果优于其他方法. 在模型压缩中,单独使用权重剪枝或卷积核剪枝,压缩后的卷积神经网络仍然存在参数冗余问题,因此提出了一种结合卷积核剪枝和权重剪枝的混合剪枝方法.通过删除不太重要的卷积核,达到压缩网络的初步目的;对剪枝过的模型再进行权重剪枝实现进一步的模型压缩;剪枝过程中通过重新训练来恢复模型精度.实验结果表明,提出的混合剪枝方法可以有效减少CNN中存在的参数冗余,实现了网络加速.进一步的工作将在更深的神经网络上进行实验以观察模型压缩的综合性能.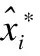
3.3 权重剪枝
4 实验结果及分析
4.1 LeNet-5剪枝结果与分析

4.2 VGG-16剪枝结果与分析

4.3 对比现有方法

5 结 论
