基于IP坐标系统的QoS优化方法

赵玉琦，李 兵，2，熊燚铭，刘 晖 ，王 静

1(武汉大学 计算机学院，武汉 430079)2(武汉大学 复杂网络研究中心，武汉 430072)3(武汉大学 国家卫星定位系统工程技术研究中心，武汉 430072)4(中国电子技术标准化研究院，北京100007)

1 引 言

随着面向服务架构的流行和分布式服务部署方式的出现，服务质量成为了当前重要的研究内容，而网络性能是影响服务质量(QoS，Quality of Service)重要因素.QoS的关键指标主要包括：可用性、吞吐量、时延、时延变化(包括抖动和漂移)和丢失，时延测量的研究可以有效提升网络性能，进而提高服务的质量.基于Ping程序的时延测量方法存在网络开销大的问题，无法满足测量需求.为了能够在保证有效快速的获取时延信息同时又仅花费较小的开销，通过预测网络节点间时延来获取实际网络中真实测量时延的近似值的方法，成为了研究热点.其中基于网络坐标系统的距离预测方案具有简单有效，开销小的特点，得到广泛的研究.

网络坐标系统是一种具有可扩展的互联网距离预测方案，该方案将网络节点距离空间映射到一个几何空间之中，每一个网络节点对应几何空间中一个坐标点，节点间距离便可以依据它们的坐标使用空间距离公式计算得出，从而把时间复杂度降低为O(N).因而，网络坐标系统能够通过复杂度为O(N)的测量，来预测N(N-1)条链路的距离，从而有效的减少了大量端到端测量[1].通过网络坐标系统，高效地获取时延，提升网络性能.

2 相关工作

在现有的预测机制当中，比较典型的研究有基于中心式的如GNP[2]、PIC[10]和基于非中心式的如NPS[11]、Vivaldi[3]等时延预测机制，上述研究内容都以如何有效快速的获取网络节点间时延作为研究重点，同时都将网络节点放入N维的坐标系统，通过计算节点坐标距离作为网络时延的预测值.GNP[2]是最早提出的网络坐标系统，将网络中节点实测时延映射到数学的几何空间上，将获取网络节点间时延转化为获取节点坐标间距离.其思想是将网络构建在一个几何空间上，如三维欧式空间，并用该几何空间中的一个点作为网络中任何一台主机的位置.

Vivaldi一种完全分布式的算法[3]，节点仅需要获得任何具有坐标的邻居节点的实测时延即可完成自身坐标的更新.Vivaldi算法是公认的具有优秀性能的网络坐标系统构建算法，其优点在于其实现是全分布式的，无需额外设立基站设施，减少了网络开支.

J.Ledlie 等人研究延迟污染现象并提出MP-Filter抑制方法[8].该方法的主要思想是基于滑动窗口滤波平滑时延，其网络坐标系统的各方面性能指标是整体最优的.MP-Filter的抑制方法在抑制随机污染方面有一定成效，但该方法舍弃了部分实测时延，没有保持原始的实测时延，这会使得其处理结果偏离实测时延，扭曲了节点坐标，使得准确度下降[9].

T-Vivaldi是对三角不等式违例(TIV)现象[5]造成网络坐标系统振荡而提出的一种对TIV进行检测和抑制的方法.其主要思想是用三角不等式条件，随机选取部分邻居节点来检测坐标更新所依据的RTT值是否构成TIV来检测违例边，并使用违例系数度量其违例程度.根据该系数的值抑制违例边对坐标的更新，从而达到了抑制TIV对坐标系统的影响的目的.

文献[6]则提出一种基于坐标抖动感知的慢启动抑制方法，将Vivaldi算法归结成非线性方程组的迭代求解算法，并且基于方程组的矛盾性提出迭代因子的自适应估计问题.其原理是将Vivaldi算法的迭代步作为子步(Sup-step)，将多个子步聚合为一个超步，在超步中感知节点当前状态，收敛过程中超步会给定一个较大的迭代步长加快收敛；收敛完成后，超步会减小迭代步长以抑制坐标抖动.

文献[15]提出了一种能量更新抑制方法(Energy Method)，该方法的主要思想是：预先设置一个开始窗口WS(Window Start)和一个当前窗口WC(Window Current)，分别用于保存节点坐标的历史记录.能量更新抑制方法适应不同的网络环境有一定的难度，计算也过于复杂，有较高的时间复杂度[9].

3 算法设计

针对在实际网络坐标系统中，由于各种随机延迟污染以及三角不等式违例现象造成网络坐标振荡等问题，本文提出了一种基于Vivaldi算法的稳定抑制Vivaldi算法(Stable inhibition Vivaldi).该算法分为三部分，第一部分是对随机延迟污染的抑制，该部分使用了本文提出的TO-Filter抑制方法，第二部分是对网络坐标抖动的检测，第三部分是对坐标抖动进行抑制.

3.1 TO-Filter方法

TO-Filter抑制方法(Timeout Filter)是本文提出的一种抑制随机延迟污染的方法，其思想参照了TCP超时重传机制，通过计算测量来获得当前RTT的一个估计值，并以该RTT估计值为基准来判定是否出现了随机延迟污染.原理是：对于节点i，获得来自节点j的每一个RTTi，j，计算MeanRTTi，j如公式(1).

MeanRTTi，j是RTTi，j的指数加权移动平均 (Exponentially Weighted Moving Average，EWMA)，这种平均能很好的反映网络的当前拥堵情况，其中α的参考值是α=0.125.同时除了计算RTT的估计值，还要计算RTT的变化.定义DevRTTi，j，用于估计RTTi，j与MeanRTTi，j的偏离程度.DevRTTi，j是RTTi，j与MeanRTTi，j的差值的EWMA，这里β的默认值为0.25.参数设置参考RFC标准.

当节点i获得来自节点j的一个RTTi，j时，其估计值为MeanRTTi，j+4·DevRTTi，j.首先进行随机延迟污染的检测，如果RTTi，j>MeanRTTi，j+4·DevRTTi，j则视为出现了随机延迟污染，此时的RTTi，j可能是极大的，不具有可靠性，此时先计算DevRTTi，j与MeanRTTi，j的值，然后让RTTi，j=MeanRTTi，j作为输出.

MeanRTTi,j=(i-α)·MeanRTTi,j+α·RTTi,j

(1)

DevRTTi,j=(1-β)·DevRTTi,j+β·|RTTi,j-MeanRTTi,j|

(2)

(3)

DevRTTi,j=(1-β)·DevRTTi,j+β·|RTTi,j-MeanRTTi,j|

(4)

MeanRTTi,j=(1-α)·MeanRTTi,j+α·RTTi,j

(5)

3.2 三角不等式违例现象以及抑制方法

三角不等式违例现象是网络坐标振荡的主要因素之一.对此，本文提出了一种坐标抖动感知方法.本文对该坐标抖动感知方法进行改进，将RTTi，j替换为MeanRTTi，j，替换的目的是减少个别不可靠的RTT对感知方法的准确性的影响，同时不采用时间片的方法，而是使用计数的方法，当累计获得N个RTT后才进行err的计算(N=|Neighbor(i)|，即节点i的邻居节点数)，让此时节点i的坐标为xi(t)，本文的坐标抖动感知方法为公式(3).

当errt>errt-1时，视为发生了抖动，则会开始执行第三部分的抑制算法.要注意的是，坐标抖动感知方法只有在RTTi，j≤MeanRTTi，j+4·DevRTTi，j时才执行，否则需要重新计数.

3.3 稳定抑制Vivaldi算法

对于节点i获得来自节点j的一个RTTi，j，稳定抑制算法的执行步骤为：

步骤1.进行初始化，让d=1，计算器n=0，让errt-1为一个极大数；

步骤2.对随机延迟污染现象进行检测，如果RTTi，j>MeanRTTi，j+4·DevRTTi，j则执行一次步骤1和步骤3，之后让RTTi，j=MeanRTTi，j后，跳转到步骤6；

步骤3.根据公式(4)和(5)计算DevRTTi，j与MeanRTTi，j的值：

步骤4.感知坐标抖动，若此时d不等于1，说明已经开始抑制算法，跳转到步骤6；否则计算器n=n+1，如果n<|Neightbor(i)|，跳转到步骤6.

步骤5.让n=0，利用公式(3)计算errt.若errt>errt-1则让d=0，否则让errt-1=errt.

步骤6.更新坐标.

4 实验实现及分析

4.1 实验数据集和实验环境

本文的时延数据来自华盛顿大学计算机科学与工程学系的King[注]https://pdos.csail.mit.edu/archive/p2psim/kingdata/数据集，该数据集有1953个节点，共97251194条记录，这些节点都有至少9个邻居节点，通过这些数据来进行随机延迟污染分析.在本实验中，两个节点之间时延获取的方式如下图1，节点间通过最邻近DNS服务器估算时延.

图1 测试数据获取方式示意图Fig.1 Schematic diagram of test data acquisition

其中时延在0-100ms之间的记录有约8830万条，约占总体90%，剩余约600万条记录在100-500ms之间，有约90万条时延记录在500-1000ms之间，1000-2000ms之间的有约64万条记录，而3000以上也有近100万条记录，这说明了随机延迟污染是普遍存在的.

4.2 实验设计

本文在Linux系统下进行仿真，Ubuntu16.04，16GB内存，代码运行环境为jdk1.7.0_67.为了检测稳定抑制Vivaldi算法的性能，本文采用的时延数据来自上述的实测时延数据集，并选取了其中231个节点，1907419条RTT记录，这些节点都有至少9个邻居节点.将1907419条RTT记录作为一次迭代，进行20次迭代.

4.3 结果分析

根据实验设计进行试验，其相对误差RE累计分布图如图2所示.从图2中可以看出，稳定抑制Vivaldi算法中，相对误差小于2的节点占了总体77.60%，而Vivaldi算法中，相对误差小于1的节点占了总体73.32%，并且稳定抑制Vivaldi算法的相对误差RE累计分布始终比Vivaldi算法高，说明了稳定抑制Vivaldi算法的准确性比Vivaldi算法更高.

除了使用相对误差RE来度量算法的准确性，本文还使用了另一种度量方法.对于节点i获得来着节点j的一个RTT，在更新完坐标后，此次更新误差为公式(6).

(6)

则对于整个网络坐标系统中的n个测量RTT，定义整体误差均值为公式(7).

(7)

则整体误差均值e反映了整个网络坐标系统的误差程度，整体误差均值e越大，网络坐标系统的误差越大.将1907419条RTT记录作为一次迭代，计算每一次迭代的整体误差均值，具体如图3所示.

从图3可以明显看出Vivaldi算法以及稳定抑制Vivaldi算法都在较少随迭代次数内随着迭代次数增加而减少整体误差，Vivaldi算法在第3次迭代后，其整体误差均值在55.14上下波动，而稳定抑制Vivaldi算法在第3次迭代后，其整体误差均值在53.29上下波动，说明了稳定抑制Vivaldi算法比Vivaldi算法有着更高的准确性，其准确性提高了3.35%.同时稳定抑制Vivaldi算法的整体误差均值一直比Vivaldi算法低，说明了稳定抑制Vivaldi算法具有比Vivaldi算法更快的收敛能力.同样将1907419条RTT记录作为一次迭代，计算每一次迭代整体抖动方差，具体如图4所示.

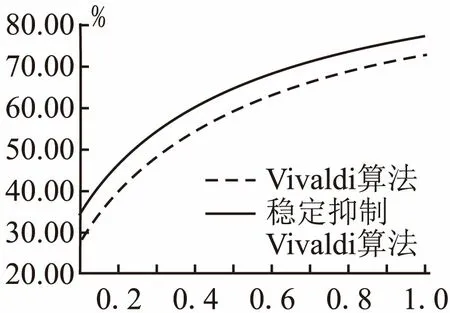
图2 相对误差RE累计分布图Fig.2 RE cumulative distribution

图3 整体误差均值Fig.3 Overall error mean

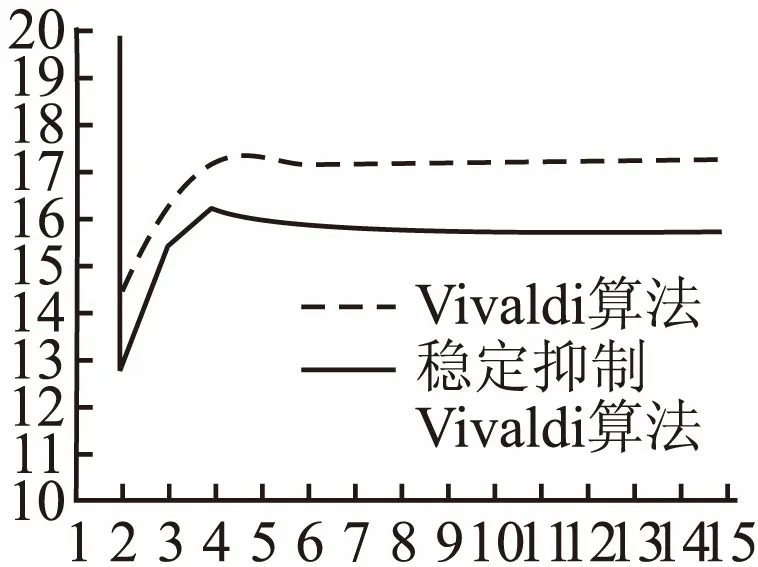
图4 整体抖动方差Fig.4 Jitter variance

图4中反应了算法刚开始执行时由于算法收敛造成坐标的剧烈变化，Vivaldi算法第一次迭代的整体抖动方差为141.35，而稳定抑制Vivaldi算法第一次迭代的整体抖动方差为222.34，这在一定程度上反应了稳定抑制Vivaldi算法有着比Vivaldi算法更快的收敛速度.而当Vivaldi算法在第7次迭代后，其整体抖动方差在17.25上下波动，而稳定抑制Vivaldi算法在第6次迭代后，其整体抖动方差在15.75上下波动，说明稳定抑制Vivaldi算法比Vivaldi算法有着更好的抑制抖动能力，其抑制效果抖动提升了8.7%.

5 结 论

网络坐标系统是一种网络节点距离预测机制，能够有效快速的获取网络节点间的时延信息，对于提升网络性能，优化网络应用有着很大的帮助.但由于网络环境的复杂，网络坐标系统受到很多因素的影响，如由于网络拥塞，网络拓扑结构发生变化，不同的数据包及其响应可能沿不同路径转发而造成的随机延迟污染，以及在将网络节点放入几何坐标系时，产生的三角不等式违例现象，都可能造成了网络坐标的动荡，降低了网络坐标系统的准确性.

Vivaldi是基于模拟的时延预测机制，是全分布式的，无需额外设立基站设施，对Internet拓扑变化有较好的适应性.然而Vivaldi对于随机延迟污染现象与TIV现象并没有很好防范策略，本文则对这两个方面展开工作：

对于随机延迟污染现象，本文介绍了随机延迟污染抑制方法MP-Filter，同时提出了TO—Filter随机延迟污染抑制方法.

其次对TIV现象，提出了稳定抑制Vivaldi算法，其特点是同时考虑随机延迟污染以及TIV现象，其思想是通过计算并保存节点获得的每一个实测时延的估计值，通过比较实测延时与估计值，来判断是否出现了随机延迟污染，同时通过计算预测延时与均值估计值的差值均值来判断是否出现了坐标抖动；在抑制抖动方法中，选择一种递减函数作为抑制函数来减少坐标更新程度.

通过搭建网络坐标系统，可以将服务中的要素在新的标准范围内度量，可以从全新的角度审视服务的发现、组合、协作、推荐和质量等.同时在网络坐标系统内，我们可以更加方便的度量服务质量中的可用性、吞吐量、时延、时延变化(包括抖动和漂移)和丢失问题.进一步，可以将构建基于时空的网络坐标系统，通过高精准定位和对时，实现对服务和服务要素的精准定位和调控.