聚类集成技术在地铁站点类型研究中的应用

游丽平,陈德旺,陈 文,刘 林

1(福州大学 数学与计算机科学学院,福州 350108)2(福州大学 智慧地铁福建省高校重点实验室,福州 350108)3(福州地铁公司运营分公司,福州 350012)

1 引 言

随着地铁建设事业的蓬勃发展,地铁线路不断增加,地铁站点的管理变得更加艰难.合理的地铁站点分类可以对站点管理提供参考,对其他交通方式的规划提供借鉴意义,同时对广告投放的地点提供参照.

国内外现有的站点类型的相关研究中均采用单一的聚类方法对站点进行分类,如Chabchoub Y等人以巴黎自行车共享系统的工作日的数据为例,采用聚类分析方法k-means,将自行车站点分为3类[1],李向楠采用k-means将成都地铁1号线分为6种类型的站点[2];岳真宏等采用高斯混合模型将北京地铁分为4 类[3];尹芹等采用时间序列聚类方法将北京地铁站点分为8类[4].

但是,对同一数据集不同的聚类算法产生的结果具有差异性,没有一种聚类算法能准确揭示各种数据集所呈现出来的多种多样的簇结构[5].基于此前提下本文提出将聚类集成方法应用于站点类型研究,与单一聚类算法相比,聚类集成可以提高聚类结果的质域和聚类的健壮性,不同的聚类结果,从不同方面反映了数据集合的结构和多个聚类算法的综合特性[6].本文将使用不同的算法对同一个数据集产生多个聚类结果构成一个聚类集体,结合聚类集成方法,以期望取得更好的效果和更强的鲁棒性[7].

2 数据来源及处理

本文研究对象为福州地铁1号线客流数据,文章选取2月13日至17日一周工作日的数据进行实验分析.福州地铁1号线一期全程24.89公里,设立21个地铁站点,站点名称及相应的编号如表1所示.

表1 站点名称及编号
Table 1 Station name and number

编号名称编号名称编号名称编号名称1象峰6树兜11达道16黄山2秀山7屏山12上藤17排下3罗汉山8东街口13三叉街18城门4火车站9南门兜14白湖亭19三角埕5斗门10茶亭15葫芦阵20胪雷21火车南

地铁站点客流数据可以反映站点自身的特性,依据这个特性,我们对其进行分类,可以对站点管理提供帮助.但是这种分类并没有明确的界限,属于无监督学习部分,在无先验知识的情况下,我们并不能判断对错.而目前解决这一类问题时均采用单一聚类方法,并不能保证高准确性.因而文章选用站点进、出站客流数据作为聚类分析的变量,结合聚类集成技术来研究站点的类型.

地铁原始客流数据一条记录包含53个信息,最后提取目标信息、刷卡日期、卡编号、设备编号、进出站编号等5个信息.借助PyCharm编辑器编写数据处理程序,计算出每个站点每天的进、出站数据.

3 聚类集成技术

在现有研究基础上,本文提出基于聚类集成的地铁站点类型研究,其过程如图1所示.

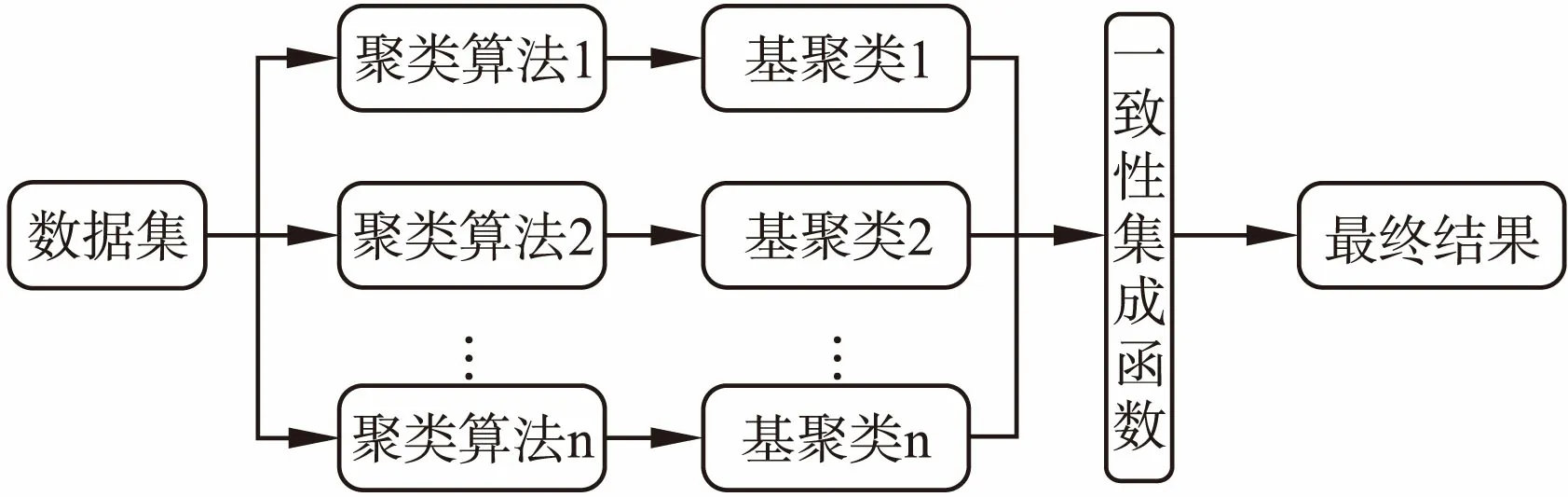
图1 聚类集成过程示意图Fig.1 Schematic diagram of clustering integration process

3.1 聚类合理性判别指标

在聚类分析中,我们希望聚类结果拥有高内聚、低耦合的性质,也就是簇内的点相似性尽可能的大,簇与簇间的点尽相

似性尽可能小.而轮廓系数(Silhouette Coefficient)就是通过这两种特性来定义的,以此来实现对聚类结果合理性的评价,它的目的是寻找簇内高内聚且簇间高分离的聚类结果.

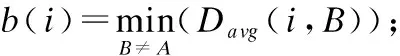
(1)

对于一次聚类的轮廓系数T则定义为式(2):

(2)

其中n为所有样本个数,轮廓系数T越接近1代表此时的内聚度和分离度相对较优,说明该样本聚类越合理,可用于聚类数目的确定[8].

3.2 生成基聚类

聚类集成是指关于一个对象集合的多个划分(partitioning)组合成为一个统一聚类结果的方法[9].而一个对象的多个划分就称为基聚类,使用不同的方法来产生基聚类,可以从不同的角度挖掘出模式间的关系[10].本文将用以下三种方法来产生基聚类:

首先,使用层次聚类方法来对数据集进行实验得到一个聚类结果.在层次聚类中采用欧式距离作为数据相似度的度量;在对两个类进行合并时,计算类与类之间距离的算法有多种,通过实验,对不同时间数据集不同算法情况下产生的二叉聚类树和实际情况的相符程度进行计算,结果如表2所示,发现在当前数据集情况下未加权平均距离法(average)表现的最优,故本文采用未加权平均距离法,也就是AL(average-linkage)层次聚类.其次,选用的是K-means聚类算法,它通过迭代算法,逐次更新各类的中心值,直至得到最好的聚类结果,即实现目标函数的最小化,其目标函数定义如公式(3)所示:

(3)

表2 不同算法情况下产生的二叉聚类树和实际情况的相符程度值
Table 2 Coincidence degree between the binary clustering tree generated by different algorithms and the actual situation

日期|方法'average''centroid''complete'median''single''ward''weighted'2.130.75280.75270.7390———0.72510.73260.74422.140.83250.83240.68690.69330.74210.65450.69332.150.78430.78430.73420.70980.65280.72450.73882.160.74720.74710.73740.70340.65340.73120.74042.170.75470.75470.74800.74920.75490.74190.7494

其中K为聚类的类数;Ci为第i个簇;p为簇内的各点;μi为第i个簇的簇中心.由于每次选取的中心值不同,聚类结果可能不尽相同,因此本文进行了多次重复实验.

最后,采用的是fuzzy c-means(FCM)算法,它是一种基于划分的聚类算法,它的思想就是使得被划分到同一簇的对象之间相似度最大,而不同簇之间的相似度最小,其目的同kmeans一样也是实现目标函数最小化,其目标函数如式及约束条件定义为式(4):

(4)

其中K为聚类的类数;n为样本个数;μij为每个样本j属于某一类i的隶属度;Ci为模糊组的聚类中心;Xj为第j个样本.

3.3 设计一致性集成函数

一致性集成函数,顾名思义就是将基聚类进行合并集成,得到一个统一的聚类结果的函数.本文将采用投票法来实现对基聚类的集成.

相对于监督式学习而言,在聚类中使用投票法进行集成更加困难,因为聚类中存在类标签对应的问题[11].例如,在数据集D中有{a,b,c,d,e}5个对象,对于该数据集有结果划分C1={1,1,2,2,3}和C2={2,2,1,1,3},这两个看似划分不同的结果实际上却是等价的,划分的聚类数目相同且都划分为{a,b},{c,d},{e}.为了解决这种类标签对应的问题,本文采用了基于共协关系矩阵(Co-association matrix)的集成方法[12].

基于共协关系矩阵的集成方法是通过计算两个数据点被基聚类划分在同一个簇中的次数来实现的,如果两个数据点被聚在同一个簇中的次数占基聚类总数的一半以上,也就是说有一半以上的聚类成员认为它们属于同一个簇,则它们被归为同一个簇.共协关系矩阵定义如下:

co_ass(i,j)=Sij/N

(5)

其中Sij表示在所有基聚类结果中样本i与样本j被划分到同一个簇的基聚类的个数;N为基聚类的总数.在共协关系矩阵的基础上利用投票法设定阈值α=0.5,当co_ass(i,j)>α时认为样本i与样本j属于同一个簇,然后利用传递性原则确定最终的聚类结果.传递性原则定义为:

{a,b}∩{b,c}⟹{a,b,c}

(6)

即若有样本a和样本b属于同一簇且样本b和样本c也属于同一簇,则可以推出样本a、b、c属于同一簇.

3.4 评价指标

本文定义了一个聚类划分的稳定性指标(Stability Indicator),该标准同一致性集成函数类似,也是通过共协关系矩阵实现,其关系矩阵定义为:

(7)

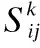
(8)

其中n表示站点总数;m为(i,j)所有组合情况即n2;num()表示符合条件的数量.Sta值越接近1则表示该算法越稳定.

4 实验结果分析

4.1 聚类数目分析

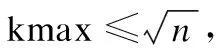
表3 层次聚类轮廓系数
Table 3 Silhouette coefficient of hierarchical clustering

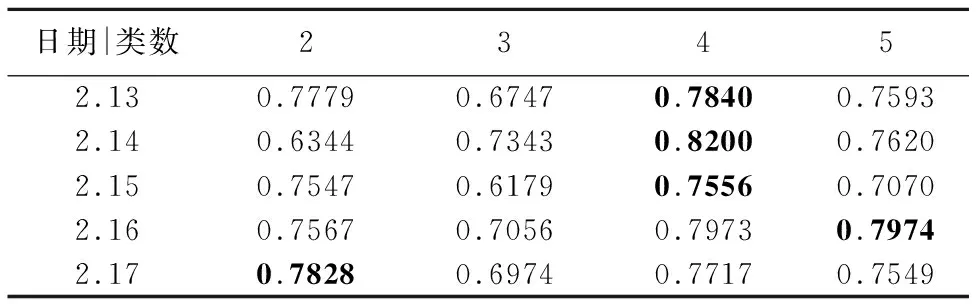
日期|类数23452.130.77790.67470.78400.75932.140.63440.73430.82000.76202.150.75470.61790.75560.70702.160.75670.70560.79730.79742.170.78280.69740.77170.7549

表4 Kmeans聚类轮廓系数值
Table 4 Silhouette coefficient of kmeans clustering

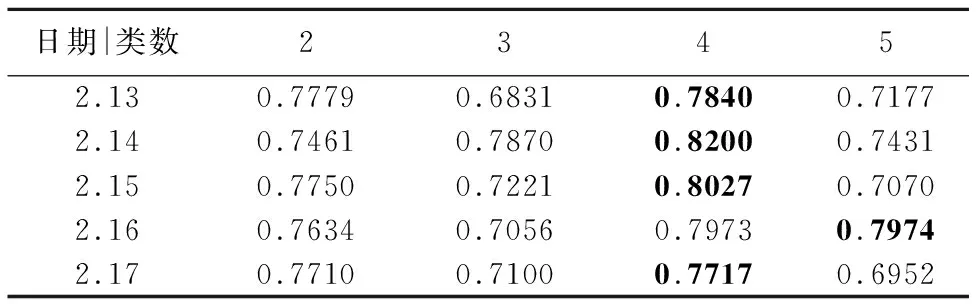
日期|类数23452.130.77790.68310.78400.71772.140.74610.78700.82000.74312.150.77500.72210.80270.70702.160.76340.70560.79730.79742.170.77100.71000.77170.6952

表5 FCM聚类轮廓系数
Table 5 Silhouette coefficient of FCM clustering

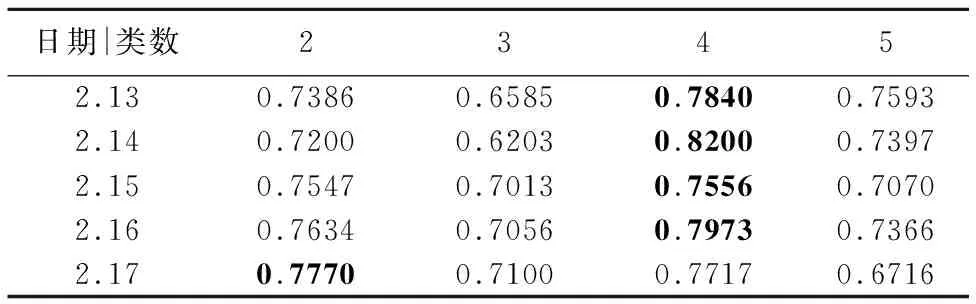
日期|类数23452.130.73860.65850.78400.75932.140.72000.62030.82000.73972.150.75470.70130.75560.70702.160.76340.70560.79730.73662.170.77700.71000.77170.6716

4.2 站点聚类分析

每种算法分别计算了从2月13日至17日数据,对于一个工作日数据集的基聚类结果将使用一致性集成函数进行第一次集成,之后为消除偶然因素的影响,将这5日每日的结果作为一个基聚类进行第二次集成,以得到最终的结果.

4.2.1 聚类结果展示

表6至表8为三种聚类方法多天的聚类结果,分类结果中的每一行为一个类,数字1-21代表站点的编号.通过对比可以发现,对于同一天的数据不同的算法可能产生不一样的划分结果.而不同的聚类算法是从不同的角度对数据集进行划分,因此聚类集成得到的结果可以结合多个算法的综合特性.表9为每个工作日的多种方法的集成结果.

4.2.2 算法稳定性分析

通过稳定性评价指标sta计算,表明聚类集成结果在该数据集情况下,稳定性比FCM、kmeans及层次聚类更加稳定.各方法指标值如表10所示.

集成算法的稳定性比最稳定的层次聚类提升了5.96%,比最不稳定的kmeans聚类提升了38.18%,在稳定性表现方面集成算法具有明显的优势.

此外,由于集成聚类结果是在几个基聚类的基础上产生的,它综合了多种算法的特性,同时也带来了相对于单个算法集成聚类计算量更大的问题.因此聚类集成比较适用于高维度的数据集,由于高维度的数据内在特性总是比较复杂,而集成可以从多角度反映数据集的结构;还可以用于虽然数据是低维度,但是簇结构比较难发现的数据集,这种时候使用集成就可以提高划分的稳定性和准确性.

表6 层次聚类结果
Table 6 Clustering result of hierarchical

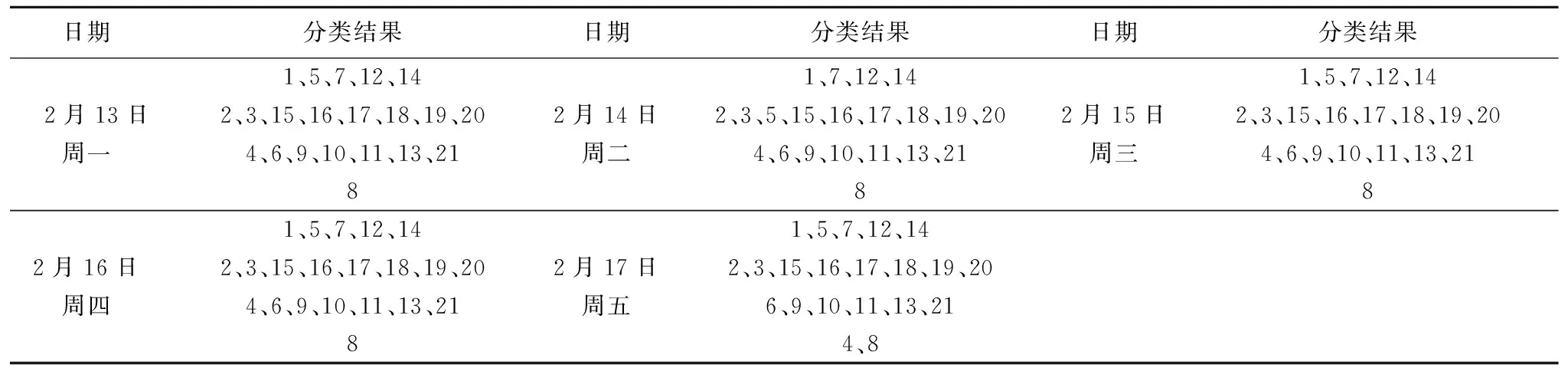
日期分类结果日期分类结果日期分类结果2月13日周一1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月14日周二1、7、12、142、3、5、15、16、17、18、19、204、6、9、10、11、13、2182月15日周三1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月16日周四1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月17日周五1、5、7、12、142、3、15、16、17、18、19、206、9、10、11、13、214、8

表7 kmeans聚类结果
Table 7 Clustering result of k-means

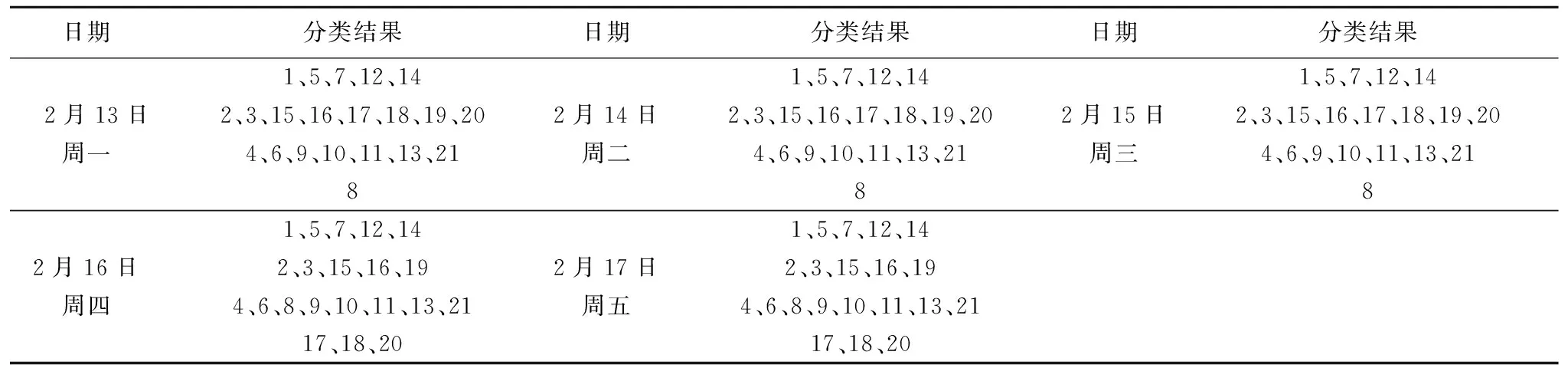
日期分类结果日期分类结果日期分类结果2月13日周一1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月14日周二1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月15日周三1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月16日周四1、5、7、12、142、3、15、16、194、6、8、9、10、11、13、2117、18、202月17日周五1、5、7、12、142、3、15、16、194、6、8、9、10、11、13、2117、18、20

表8 FCM聚类结果
Table 8 Clustering result of FCM

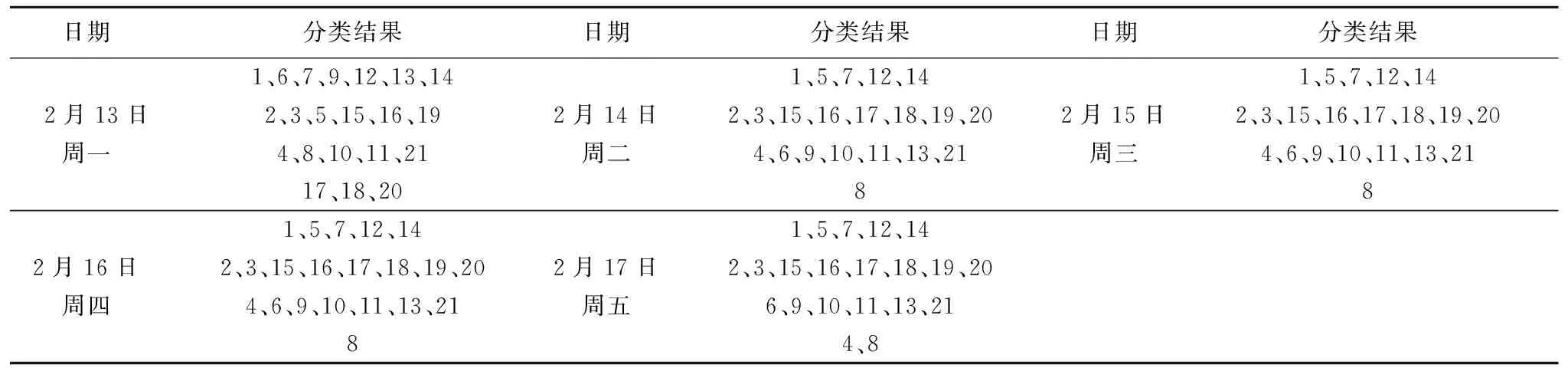
日期分类结果日期分类结果日期分类结果2月13日周一1、6、7、9、12、13、142、3、5、15、16、194、8、10、11、2117、18、202月14日周二1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月15日周三1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月16日周四1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月17日周五1、5、7、12、142、3、15、16、17、18、19、206、9、10、11、13、214、8

表9 5个工作日的多种方法的集成结果
Table 9 Integration result of multiple methods on 5 working days

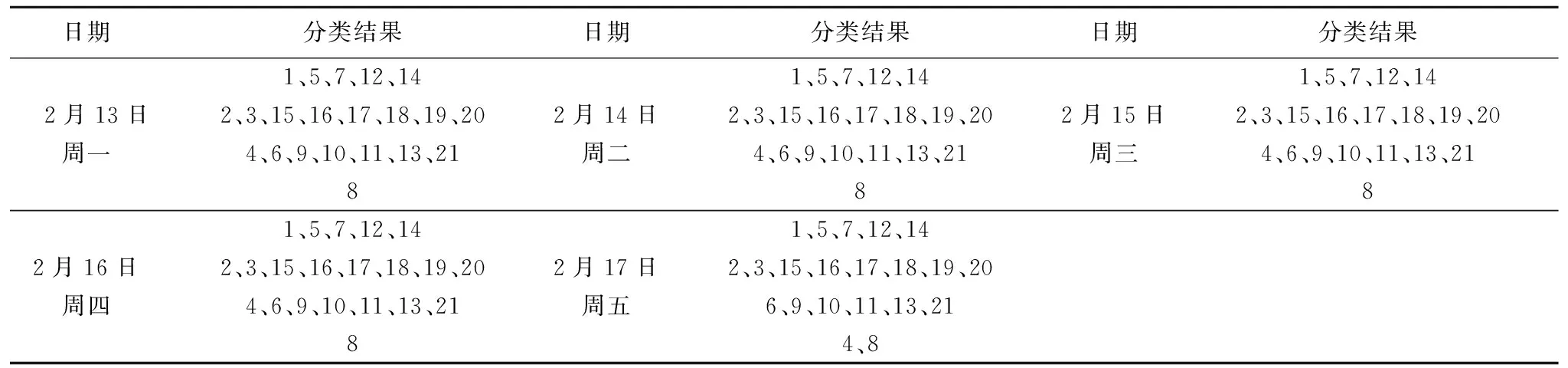
日期分类结果日期分类结果日期分类结果2月13日周一1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月14日周二1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月15日周三1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月16日周四1、5、7、12、142、3、15、16、17、18、19、204、6、9、10、11、13、2182月17日周五1、5、7、12、142、3、15、16、17、18、19、206、9、10、11、13、214、8

4.2.3 集成结果分析

表11在5个工作日的多种方法的集成基础上进行第二次集成得到多个工作日的综合集成分类:该结果经与福州地铁集团工作人员确认,认为站点分类结果科学有效,对于合理安排人力非常有参考价值.

簇标签2为低流量站点包含8个站点,分别为葫芦阵、黄山、排下、城门、三角埕、胪雷、秀山以及罗汉山.这类站点都是距离市中心比较远,客流量明显较少,主要是一些工厂、汽车销售公司等比较多.此类站点交通方式的衔接和站点管理都比较轻松,适当就好.

表10 稳定性指标值
Table 10 Stability index value

算法 Sta值FCM聚类0.7506层次聚类0.9138 kmeans聚类0.7007集成聚类0.9683

簇标签1为中流量站点包含5个站点,分别为象峰、斗门、屏山、上藤及白湖亭.这类站点客流量适中,地铁压力不大.

簇标签3为高流量站点包含7个站点,分别为火车站、树兜、南门兜、茶亭、达道、三叉街及火车南站.这类站点是交通枢纽中心或是距离市中心近人口住宅密集的点,人口密集,客流量大.此类站点是除东街口外最高客流量点,客流压力大,在站点管理和交通规划时都要加强关注.

簇标签4为超高流量站点包含东街口站.东街口是一个福州市最繁华的商业街区,人流量多,地铁乘客流量大.这类站点需要重点关注、加强管理,多增加人手.在这些站点的周围应该多一些交通方式,可以减少地铁高峰时期的压力.此外,这类站点附近也是最优的广告投放点.

表11 多个工作日的综合集成分类
Table 11 Integrated classification of multiple working days

站点编号123456789101112131415161718192021簇标签122313143331312222223

5 结束语

在现有站点聚类研究均采用单一聚类方法的基础上,本文提出了基于聚类集成的站点类型研究,运用层次聚类,K均值聚类以及FCM聚类三种聚类方法产生的结果作为聚类集体,通过基于共协关系矩阵的集成方法以及传递性原则实现聚类集体的合并.

定义了聚类划分稳定性指标sta,通过指标计算表明在该数据情况下,聚类集成方法在几种聚类方法中表现最为稳定.通过实验分析,将福州地铁1号线分为了超高流量站点、高流量站点、中流量站点以及低流量站点4类.

本文只是针对工作日的站点类型进行研究,在之后的研究中将结合节假日的客流情况进行地铁站点类型的探讨,分析节假日与工作日的区别;此外,对影响站点类型因素的考虑也不够全面,在今后的研究中也将要解决这个问题.