联合贝叶斯估计与深度神经网络的语音增强方法

黄张翼,周 翊,舒晓峰,刘宏清

(重庆邮电大学 通信与信息工程学院,重庆 400065)

1 引 言

随着人工智能的快速发展,语音识别技术日趋成熟,在各种终端上的应用也越来越广泛[1].语音增强作为语音识别的前端,能消除各类噪声干扰以提升识别率,其作用愈发重要.传统的经典语音增强算法主要有谱减法[2]、维纳滤波法[3,4]、基于统计的MMSE(minimum mean square error)幅度谱估计法[5]、基于子空间法[6]等.这些传统的基于统计模型的语音增强算法通常会残留一部分噪声,比如音乐噪声,也容易引入非线性失真.尤其在低信噪比条件或非平稳噪声环境下,传统语音增强算法的效果不够理想.

近年来,基于深度学习的研究方法成为语音增强的热点[1].2006年,Hinton提出了深度神经网络(deep neural network,DNN)的概念[7],深度神经网络通过大数据训练,较传统算法能够更好地表示语音和噪声之间的非线性关系.根据训练目标的不同,基于深度神经网络的语音增强方法可分为基于映射和基于掩蔽的语音增强方法.2015年,Xu等人提出一种基于回归深度神经网络的语音增强模型[8],采用对数功率谱作为训练特征,DNN作为映射函数,从而对纯净语音进行预测.Nie等人考虑了语音的时频特性,提出将非负矩阵分解(NMF)与DNN相结合的语音增强方法[9].Huang等人提出将掩蔽融合到目标语音的幅度谱估计中,其最终目标是估计语音幅度谱,而不是时频掩蔽[10].Han等人提出联合优化DNN与维纳滤波法[11],利用维纳滤波平衡失真和残留噪声,在低信噪比下有效提升语音感知质量.

训练目标在基于深度神经网络语音增强训练中起着重要作用,所以输入的特征的质量是一个不容忽视的重要问题.文献[12]证明了增强后的语音特征相对原始特征能更好地提升神经网络的语音增强效果.因此本文提出一种Chi分布下基于听觉感知广义加权的贝叶斯估计器,并将其作为预训练与深度神经网络进行结合.首先,使用Chi分布下基于听觉感知广义加权的贝叶斯估计器提取带噪语音幅度谱作为深度神经网络的输入特征.然后,通过该网络对输入的增强幅度谱进行训练分别得到对纯净语音和噪声的幅度谱估计,计算时频掩蔽估计出增强后语音幅度谱作为网络的输出.最后利用带噪语音的相位进行波形重构,合成可测听的语音文件.

2 Chi分布下基于听觉感知广义加权的贝叶斯估计器

相比于传统的瑞利假设,纯净语音的傅里叶系数更好地符合Chi分布[13].同时,在实际的生活中,人的听觉系统对语音能量较高位置的量化噪声的感知不是特别敏感,量化噪声会被语音信号适当地掩蔽.所以我们利用人耳的掩蔽特性,并且假设纯净语音的傅里叶系数服从Chi分布,可以推导出一个在Chi分布下基于听觉感知广义加权的贝叶斯估计器.具体推导流程如下:

采样得到的带噪语音信号可以表示为:

y(n)=x(n)+d(n)

(1)

其中,x(n)表示纯净语音信号,d(n)表示加性噪声信号.将其变换到频域可得:

Y(λ,k)=X(λ,k)+D(λ,k)

(2)

Y(λ,k),X(λ,k) 和D(λ,k)分别表示第λ帧和第k个频点.使用极坐标可表示为:

R(λ,k)ejθR(λ,k)=A(λ,k)jθA(λ,k)+N(λ,k)jθN(λ,k)

(3)

R(λ,k)、A(λ,k)和N(λ,k)分别为带噪语音信号、纯净语音信号和噪声信号在频点k的幅度.θR(λ,k)、θA(λ,k)和θN(λ,k)分别为三者在频点k的相位.

因为语音信号的傅里叶系数更好地符合Chi分布.所以我们假设语音的傅里叶系数服从Chi分布:

(4)

其中2a表示Chi分布的自由度,λx=aθx,α为语音的相位信息.λx表示纯净语音信号傅里叶系数的方差.由于噪声类型繁多,单一模型无法描述所有种类的噪声.所以,本节仍然采用高斯模型假设描述噪声信号,设噪声信号的傅里叶变换系数服从复高斯分布:

(5)

(6)

将我们的改进的语音模型公式(4)、(5)代入(6)经过公式推导可以得到Chi分布下基于听觉感知特性广义加权的贝叶斯估计器:

(7)

增益函数为

(8)

其中ν,υa和ξa的定义如下:

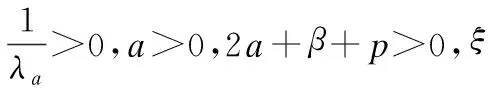
3 联合Chi分布下听觉感知广义加权的贝叶斯估计与深度神经网络的语音增强方法

本文在推导出Chi分布下基于听觉感知广义加权的贝叶斯估计器的基础上,进而提出联合改进的贝叶斯估计与深度神经网络的语音增强算法.将提出的新型网络命名为GW-Chi-DNN.

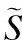
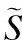
(9)

(10)

4.用误差逆传播(error BackPropagation,BP)算法更新网络权值,使用纯净语音特征S作为网络训练的标签.基于最小均方误差的代价函数为:

(11)

权值更新公式为:

(12)

其中,η是学习率.根据链式法则,可知:

(13)

(14)

根据神经网络结构定义可得:

(15)

(16)

将式(13)、(14)、(15)、(16)代入(12),即可得到△ω更新网络权值.

图2给出了GW-Chi-DNN模型的系统框架.整个系统包括训练阶段和增强阶段.在训练阶段,首先使用Chi分布下改进的基于听觉感知广义加权的贝叶斯估计器预处理特征,接着联合训练含掩蔽的DNN网络,利用纯净语音幅度谱作为标签对网络进行有监督的训练.在增强阶段,训练完成的神经网络被用来估计增强后的语音幅度谱.因为人耳对小相位的畸变不敏感,所以可以直接从带噪语音中提取相位信息并进行短时傅里叶逆变换重构得到时域的增强语音信号.最后采用重叠相加的方法合成语音波形.

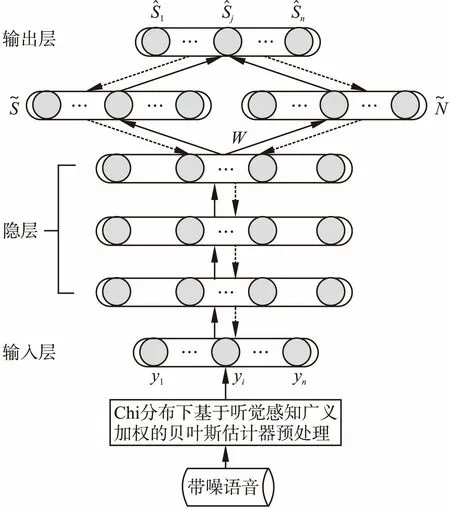
图1 GW-Chi-DNN结构图Fig.1 Architecture of GW-Chi-DNN

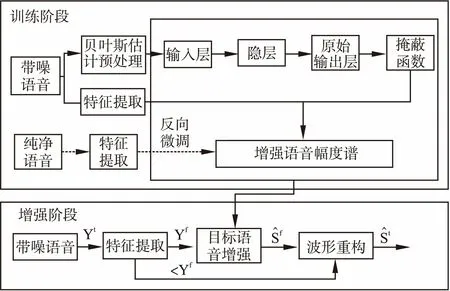
图2 GW-Chi-DNN系统流程图Fig.2 System of GW-Chi-DNN

4 实验仿真

4.1 Chi分布下改进的的贝叶斯估计器实验

为了验证第2节提出的Chi分布下基于听觉感知广义加权的贝叶斯估计器(GW-Chi-STSA)的性能,我们分别选取传统的基于听觉感知广义加权的贝叶斯估计器(GW-STSA)和加权欧式失真测度的幅度谱估计器(WE-STSA)作为参考比较的方法.测试语音是来自NOIZEUS数据库中的随机30段语音,16kHz采样,帧长为512.测试噪声是来自NOISEX-92噪声库白噪声、粉红噪声、babble噪声和工厂噪声.测试三种算法在0、5、10、15dB四种不同噪声下的分段信噪比和PESQ值[14].

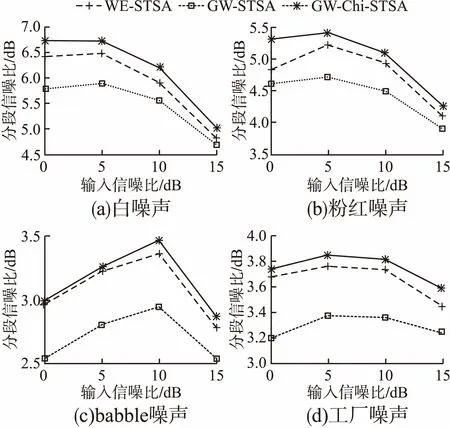
图3 三种算法的分段信噪比提升值Fig.3 SegSNR improvement of three algorithms

图3和图4分别是经过三种算法增强后的分段信噪比提升值和PESQ提升值.从图3中可以看出,经GW-Chi-STSA算法增强后的语音分段信噪比提升效果明显高于其余两种算法.白噪声和粉红噪声的提升效果更好,而babble噪声和工厂噪声提升效果相对不明显.这是因为传统语音增强算法需要对噪声进行估计,白噪声和粉红噪声是平稳噪声,babble噪

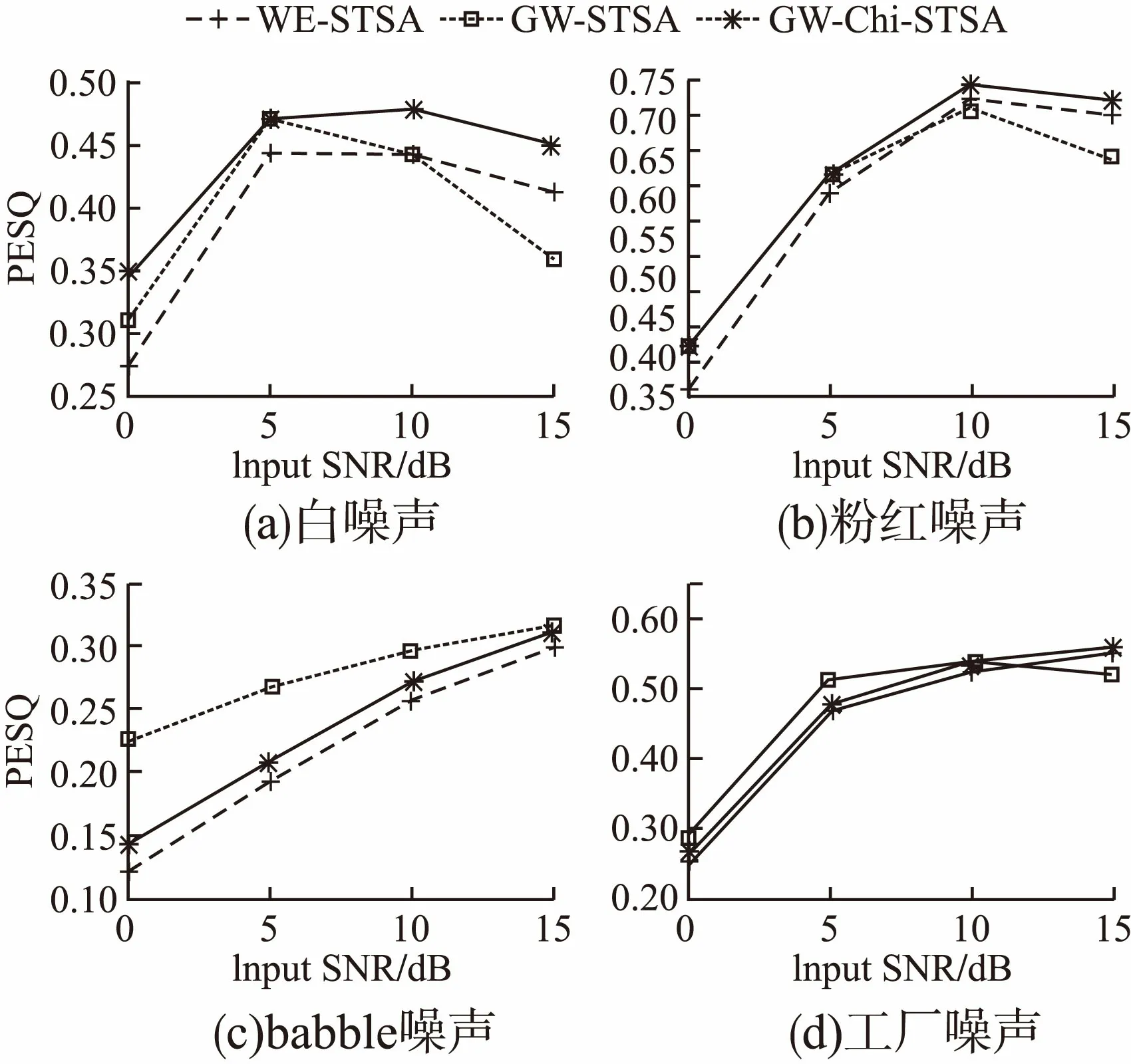
图4 三种算法的PESQ提升值Fig.4 PESQ improvement of three algorithms

声和工厂噪声属于非平稳噪声,通常对非平稳噪声的估计是比较困难的.在图4中,经GW-Chi-STSA算法增强后的babble噪声和工厂噪声同样性能欠佳.但是针对白噪声和粉红噪声处理后的PESQ结果均有提升.综上,相较于传统贝叶斯估计器,Chi分布下基于听觉感知广义加权的贝叶斯估计器能够取得更优的性能,后续工作对非平稳噪声的抑制还需做进一步的优化.

4.2 联合贝叶斯估计与深度神经网络的语音增强算法实验

4.2.1 实验数据及评估方法

为了评估本文提出的联合深度神经网络与Chi分布下基于听觉感知广义加权的贝叶斯估计的语音增强算法(GW-Chi-DNN)的性能,我们分别选取不采用预处理的基于深度神经网络的语音增强算法(DNN)和Chi先验下基于听觉感知广义加权的贝叶斯估计器(GW-Chi-STSA)作为参考比较的方法.

在实验的训练阶段,我们选取使用TIMIT数据集中的4000条纯净语音,训练噪声为8种噪声类型,分别是Car,Street,Restaurant,Airport,Train,Subway,Babble和Drill.训练语音由4000条纯净语音按照-5dB、0dB、5dB和10dB四种不同的信噪比混合8种噪声得到训练语音数据.混合过程是随机地从4620条纯净语音和8种噪声中各选一条,然后随机截取整段噪声中的部分噪声与纯净语音按照4种信噪比进行混合得到最终的训练语音.

将混合好的带噪语音的幅度谱作为GW-Chi-DNN网络的输入.所有语音数据均采用16kHZ的采样率,帧长取512,对每帧语音加汉明窗,相邻帧间的重叠为50%.GW-Chi-DNN网络隐层层数设为3层,每层1024个节点,中间层激活函数选择ReLU函数,输出层激活函数选择Linear函数.

测试集语音从TIMIT数据集中剩下的620条语音中随机抽取200条进行合成.噪声数据采用与训练集噪声不相同的Noisex92噪声库中的white、pink、factory和engine噪声.对于每一类噪声,将200条语音分别按照-5dB、0dB和5dB的全局信噪比与该类噪声的随机截取片段进行混合.

测试指标为频域分段信噪比fwSNRseg、STOI和PESQ.其中,频域分段信噪比的定义如下:

(17)

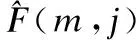
4.2.2 实验结果

为了比较DNN、GW-Chi-STSA和GW-Chi-DNN这三种方案的语音增强性能,我们分别选用三种方法对同样的测试集语音进行增强,进而对增强语音的清晰度和可懂度进行比较.

表1和表2从左至右分别给出了未经过增强的训练集带噪语音和经过三种方法增强过的带噪语音信号的平均PESQ和STOI得分.通过横向对比我们可以发现,三种语音增强方法均能有效地提高语音质量,但是GW-Chi-DNN方法下的PESQ和STOI值是最高的.这说明本文提出的GW-Chi-DNN方法优于DNN方法和GW-Chi-STSA方法.

此外,我们还在表3中给出了带噪语音和增强语音的频域分段信噪比,它比全局信噪比更接近实际的语音质量.与表1和表2的分析结果一致,采用GW-Chi-DNN方法增强后的语音的平均频域分段信噪比提升值最大,效果最优.同时,可以观察到,GW-Chi-DRNN网络对engine和factory这样的非平稳噪声的提升效果高于白噪声和粉红噪声,一定程度上弥补了Chi分布下基于听觉感知广义加权的贝叶斯估计器对于非平稳噪声效果较差的缺陷.

表1 三种方法的平均PESQ得分
Table 1 Average PESQ score of three methods

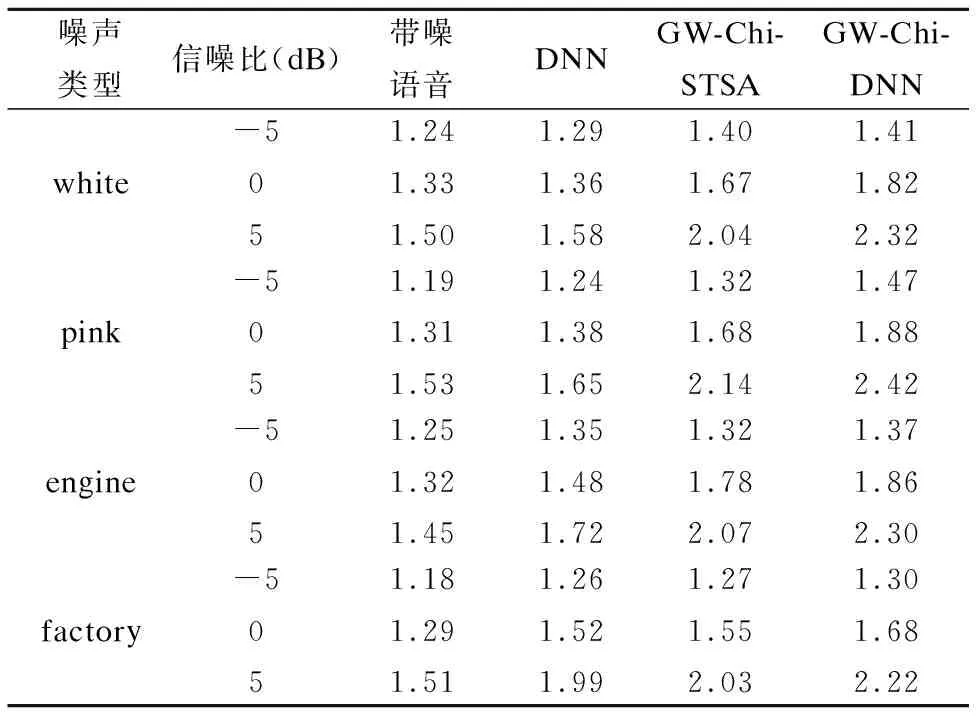
噪声类型信噪比(dB)带噪语音DNNGW-Chi-STSAGW-Chi-DNNwhite-5051.241.331.501.291.361.581.401.672.041.411.822.32pink-5051.191.311.531.241.381.651.321.682.141.471.882.42engine-5051.251.321.451.351.481.721.321.782.071.371.862.30factory-5051.181.291.511.261.521.991.271.552.031.301.682.22

表2 三种方法的平均STOI得分
Table 2 Average STOI score of three methods

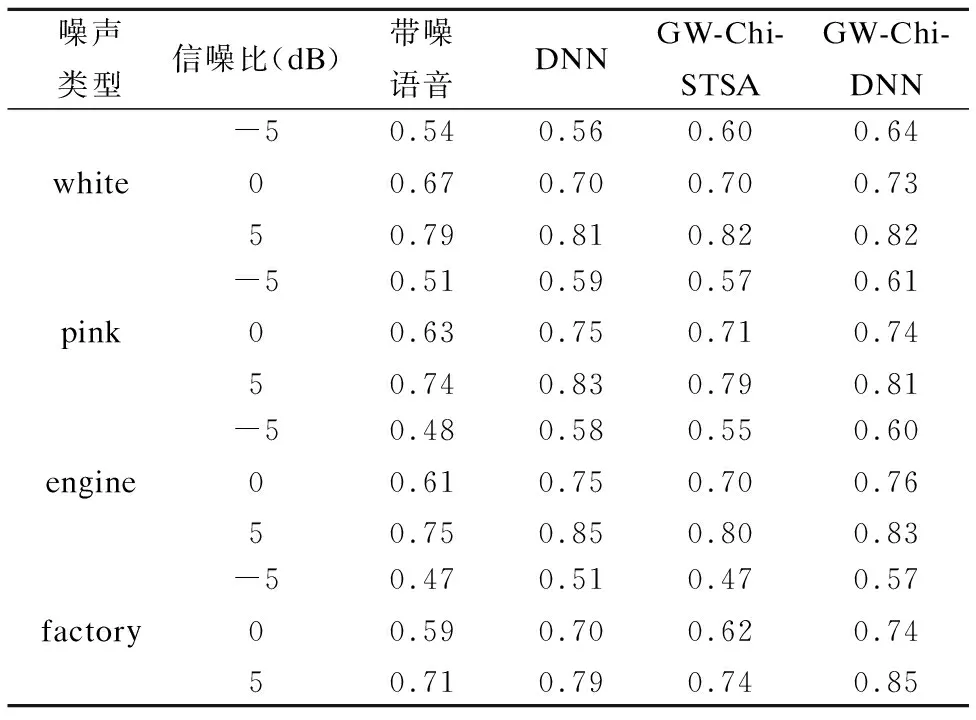
噪声类型信噪比(dB)带噪语音DNNGW-Chi-STSAGW-Chi-DNNwhite-5050.540.670.790.560.700.810.600.700.820.640.730.82pink-5050.510.630.740.590.750.830.570.710.790.610.740.81engine-5050.480.610.750.580.750.850.550.700.800.600.760.83factory-5050.470.590.710.510.700.790.470.620.740.570.740.85

表3 三种方法的平均频域分段信噪比
Table 3 Average fwSNRseg score of three methods

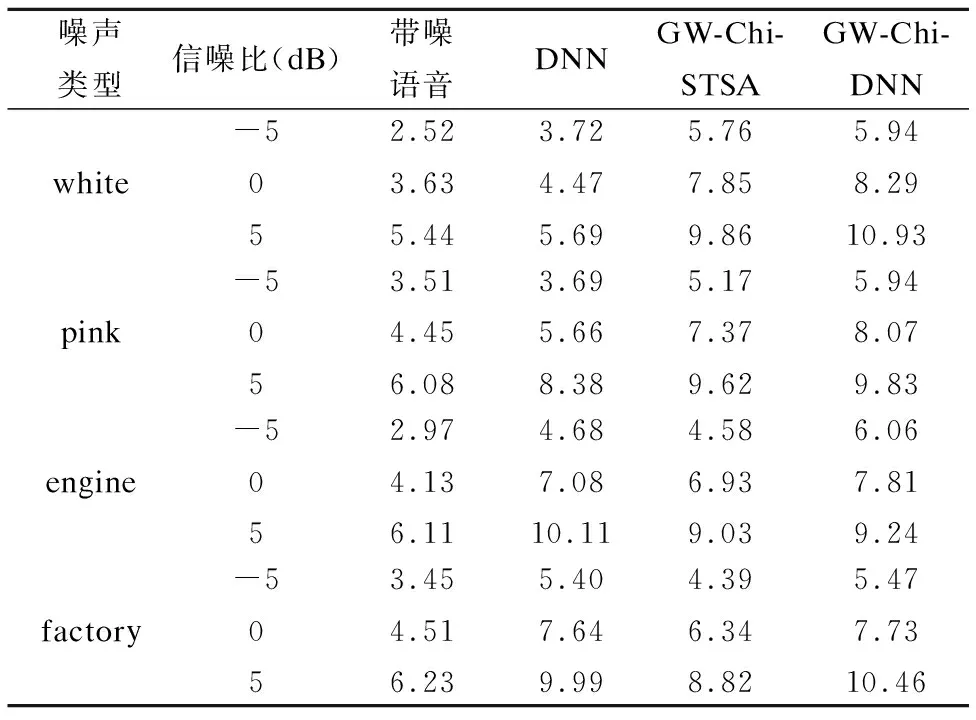
噪声类型信噪比(dB)带噪语音DNNGW-Chi-STSAGW-Chi-DNNwhite-5052.523.635.443.724.475.695.767.859.865.948.2910.93pink-5053.514.456.083.695.668.385.177.379.625.948.079.83engine-5052.974.136.114.687.0810.114.586.939.036.067.819.24factory-5053.454.516.235.407.649.994.396.348.825.477.7310.46

为了更加直观地观察增强语音信号的细节特征,我们分别采用三种方法对同一段含有粉红噪声信噪比为0dB的带噪语音进行语音增强,然后比较其增强语音的语谱图,如图5所示.

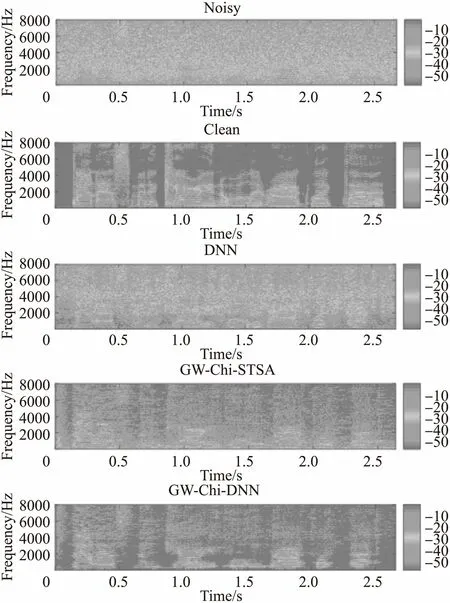
图5 增强后语谱图Fig.5 Enhanced speech spectrograph

图5自上到下分别给出了带噪语音与其相应的纯净语音的语谱图,采用DNN、GW-Chi-STSA以及GW-Chi-DNN增强后语音的语谱图.可以看到,经过DNN方法降噪后的语音语谱图仍残留大量噪声,听感较差.经过GW-Chi-STSA方法降噪后噪声残留明显减少,但经GW-Chi-DNN增强后语音的残留噪声最少,更接近纯净语音的语谱图.GW-Chi-DNN方法较好地保持了语音信号的谐波特性,具有较好地还原能力,有效地提高了语音的清晰度和可懂度.

5 结 语

本文首先在Chi分布假设下提出了一个基于听觉感知广义加权的贝叶斯估计器,并在此基础上进而提出了一种结合深度神经网络结构的语音增强算法.考虑到语音的特征特性,将本文提出的贝叶斯估计器作为带噪语音的特征提取器,可获得比原始特征输入更好的效果.实验结果表明,提出的新型神经网络结构在多数噪声环境下获得了提升的降噪性能.