货币面值的秘密
2019-01-23竹林风
竹林风
消费是我们日常生活中必不可少的一部分,我们每次消费都会跟钱打交道。但你发现了吗?现今我国使用的货币面值只有1角、5角、1元、5元、10元、20元、50元和100元。为什么货币面值没有出现3,4,6,7,8,9这些数呢?
重要数和非重要数
其实,货币面值是依据数学的组合原理来设置的。国家发行货币会遵循这样的原则:用尽量少的币值单位来组合成各种金额,以减少货币的流通量,节省流通和印制费用。所以,最高货币面值与其他面值之间要成整倍数关系,并且各货币面值能够通过简单的运算得到其他金额。而1~10这些数有“重要数”和“非重要数”之分,其中1,2,5,10是“重要数”,用这几个数能以较少的加减运算得到另外一些数。
2+1=3
2+2=4
5+1=6
5+2=7
5+2+1=8
5+2+2=9
看到了吧,1,2,5能组成3,4,6,7,8,9,所以货币面值没有出现它们的身影也是合理的。另外,发行10元后,通过“10-2=8,10-1=9”能更方便地解决8元和9元的支付问题。在现实生活中,当出现需要支付8元或9元的情况,大多数人会更愿意掏出一张10元给对方找零。
罕见的“3元”
不过,我国在1955年发行的第二套人民币中出现过3元,但它仅在市场上流通了9年。说到3元,你可能就有疑惑了:既然发行过3元,为何后面又取消了呢?
我们来玩一个排列组合游戏,你就明白了。
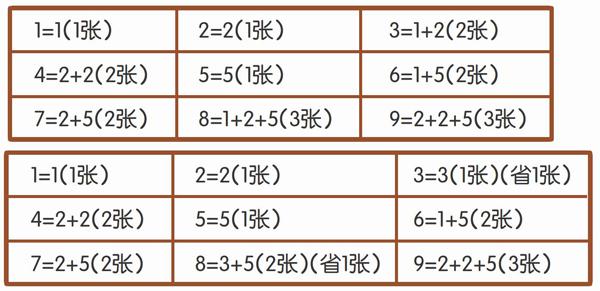
举个例子,现在利用1元、2元、5元的纸币,可以在3张之内组成1元~9元:
假设这个时候我们手上多了3元的纸币,但1元~9元的组成基本没变,节省不了多少纸币:
你看,用上了3元纸币只节省了2张纸币,而为了多印一种3元纸币,所花费的制造、流通成本可就多了。在日常生活中,1元、2元、5元、10元已经足够组成1元~9元,找零也方便,而以其10倍发行的10元、20元、50元、100元等大面值是为了更方便我们的现金使用,毕竟消费金额可不只是10元之内,成千上万都有可能。随着国家经济发展和物价上涨,2元纸币的使用频率越来越低,所以,在1999年6月30日我国停止發行2元纸币。
总结一下,选用当前面值组合是为了节约成本和简化货币结算的复杂度。
不过,某大学计算机系的一位研究员杰弗里提出了不同的观点,他认为这样的面值组合不是最优的,觉得组合应该包含16元和33元,这样能减少消费时所使用的纸币张数。
情况真如杰弗里说的那样吗?
程序运算出来的“环保组合”
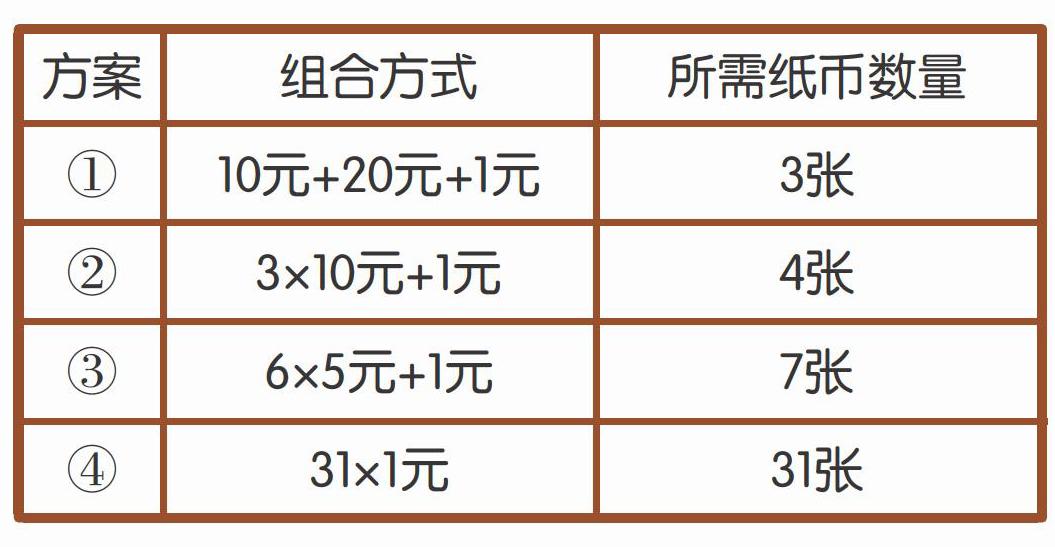
平时我们去超市买东西,支付100元以下(1元~99元)金额需要用1元、5元、10元、20元、50元五种面值组合而成,有时需要1张,有时需要2张或者更多。比如支付31元,在不设找零的情况下,有以下几种组合方式可选:
由上表可知,“10元+20元+1元”是最佳支付组合,它最节省纸币张数,也就是说,凑成31元至少需要3张纸币。
我们可以分别算出1元~99元每个金额至少需要的纸币张数,这样就能知道使用这五种面值组成 99个金额平均需要多少张纸币了。
例如:组成31元至少需要3张纸币,即10元+20元+1元;组成32元至少需要4张纸币,即10元+20元+1元+1元;组成33元至少需要5张纸币,即10元+20元+1元+1元+1元。那么组成31元、32元、33元平均需要(3+4+5)÷3=4(张)纸币。
接下来,杰弗里把“1元、5元、10元、20元、50元”更改为其他数值,最后得到“1元、5元、16元、23元、33元”这个面值组合“最环保”,用它们组成1元~99元中的每个金额平均仅需要3.29张纸币。
其他组合虽理想,但并不适用
看出来了吗?杰弗里的计算方法有漏洞,那就是假定了1元~99元中每个金额出现的频率一样,但在现实交易中,小金额出现的概率会更大一些。所以,其得到的“最佳组合”并不切合实际。
除了杰弗里,其他人也琢磨过货币面值组合问题,有人模仿信息编码方式(二进制)设计出这样的组合:1元、2元、4元、8元、16元、32元、64元。这个组合虽然不能保证每次付款时使用的纸币张数最少,但它的神奇之处在于带齐一套(即每种面值各一张)就可以组成1元~127元中的任意金额。
还有人考虑了找零情况,将面值组合设置为:1元、3元、9元、27元、81 元……以此实现“每样一张,找零无忧”。比如支付20元,你需要给收银员一张27元和一张3元,而他会找给你一张1元和一张9元,整个交易过程中,每种面值仅出现一次。
人们提出的各种货币面值组合看起来很好,但是极少被掌管货币发行的金融家们采纳。为什么呢?估计你也看出来了,那些组合需要使用者具备很强的计算能力,数学一般的人用起来肯定苦不堪言,买点东西算钱要算上好一阵子,太不方便了!
综合考虑,“1元、5元、10元、20元、50元、100元”的面值组合最符合人们的日常计算习惯。不过,随着科技发展,大家越来越多地使用电子支付,多年后该组合会怎样变化还说不定呢。
