不同运行状态下的城市桥梁标准疲劳车模型研究

2019-01-23赵信李天华张可佳白文英

重庆建筑 2019年1期

赵信，李天华，张可佳，白文英

（1大邑县公路建设服务中心，四川大邑 611330；2新疆城建试验检测有限公司，新疆乌鲁木齐 830099）

0 引言

绝大部分城市桥梁无论交通量还是车辆超载、超限等交通状况都与公路桥梁存在着明显差异，根据《公路桥涵设计通用规范》（JTG+D60-2015）[1]中针对公路桥梁不同构件及连接分别提出的3种疲劳荷载计算模型来进行城市桥梁的疲劳设计不尽合理。鉴于英国BS5400规范[2]中规定“对于总重小于30kN的车辆由于其产生的疲劳效应甚小而不予以考虑”，故我国对于标准疲劳车的研究主要集中在交通量大且超载超限频繁的公路桥梁及小部分城市桥梁。然而目前我国各大中城市频发的车辆怠速拥堵增加了城市桥梁承受重载的频次和承受超载运营的风险，因此不仅应对城市桥梁标准疲劳车进行单独研究，更应重视拥堵状态下的标准疲劳车的研究。

目前国际上对桥梁疲劳验算所用的车辆荷载一般有3种形式[3]：①车辆荷载频值谱，统计分析各种典型车辆在所调查的公路桥梁上的荷重和出现的频率；②一辆标准疲劳车，它是由第1种形式通过等效损伤原理进一步简化而来；③采用静力强度设计时标准活载中的一辆重车。桥梁的疲劳是由于日常各种载重的车辆反复作用引起的累计损伤过程，采用此法计算不符合实际交通状况。

文献[4-5]均是根据实际交通流量调查，采用等效疲劳损伤原理最终得出代表该地区的几种典型车辆荷载模型。此法对于公路桥梁来说，由于其交通的复杂性、随意性以及交通调查困难等原因，仅仅根据交通调查得出车辆荷载的频值谱，可能对于实际疲劳设计的参考价值不大。但对城市桥梁来说，交通车辆类型较为单一和固定且交通调查手段多种多样，故采用此法可有效地对城市桥梁标准疲劳车辆进行研究。

推导适用于拥堵条件下的城市桥梁标疲车模型的基础和关键在于准确获取怠速拥堵数据来建立城市桥梁的车辆荷载谱和怠速拥堵模型，此外亦可通过统计整理怠速拥堵数据获取的车辆荷载频谱值来推导车辆一般运行状态下的城市桥梁标疲车模型。故本文主要通过调查采集处于市中心限行载重货车的乌鲁木齐某高架桥车辆拥堵数据，推导出可适用于其它地区同类型城市桥梁在车辆不同运行状态下的标疲车。

1 拥堵数据采集及车辆荷载频谱

目前，获取拥堵数据的方法主要有两种：一是桥梁动态称重（B-WIM）系统[6]。在桥头安装WIM系统来测量和收集轴数、轴重、轴距、车辆达到时刻和车质量等数据，有效提高调查工作的效率和数据的准确性，但此系统主要适用于公路桥梁且针对不同的桥梁需单独设计。为保证数据的有效性，还要求在数据采集过程中桥梁在车辆荷载作用下的结构响应应尽量大；二是统计归纳法。通过查阅和收集城市常见车型的具体参数（车长、车宽、轴重、轴距、整备质量等），统计归纳出各类代表车型荷载谱，再假设车距来建立车辆拥堵模型，此法并不能真实反映实际的拥堵状况。

要确定怠速拥堵车列模型，最主要是需获得车间轴距、轴距、轴重及车重参数，因此本文提出一种经济适用的人工现场采集交通荷载参数的方法，通过照相机获得不同怠速拥堵车列的图像信息，然后运用一定的技术手段将图像信息数字化。采用此法在乌鲁木齐市某高架桥上采集获取的3个月实地车辆拥堵荷载数据库中，识别了160种具体车型并将其归为3类车型即小汽车和中、大型客车。记录的车辆拥堵荷载参数信息有车型（车长、车宽、轴距、轴重）、车-桥距、车间轴距，对这些参数样本进行统计分析从而获得各参数的统计特征值。在此基础上建立了包含3种典型车型的城市车辆荷载谱，如图1所示。并且拟定6种典型的城市桥梁怠速车辆拥堵荷载模型（具体过程参见文献[7]）。

图1 车辆荷载谱

由于桥梁处在主城区，交通管制等原因导致车辆类型比较固定且单一，因此将车型分为普通汽车、SUV、MPV和中大型客车。本文共识别出102种具体的普通小汽车车型、40种具体的SUV车型、12种具体的MPV车型和6种中大型客车车型，取各类车型的轴重和轴距的均值来作为其代表值并且假定前后轴重相等，由此可得实桥不同车模型、频数和占比，见表2。

表1 怠速车辆拥堵模型

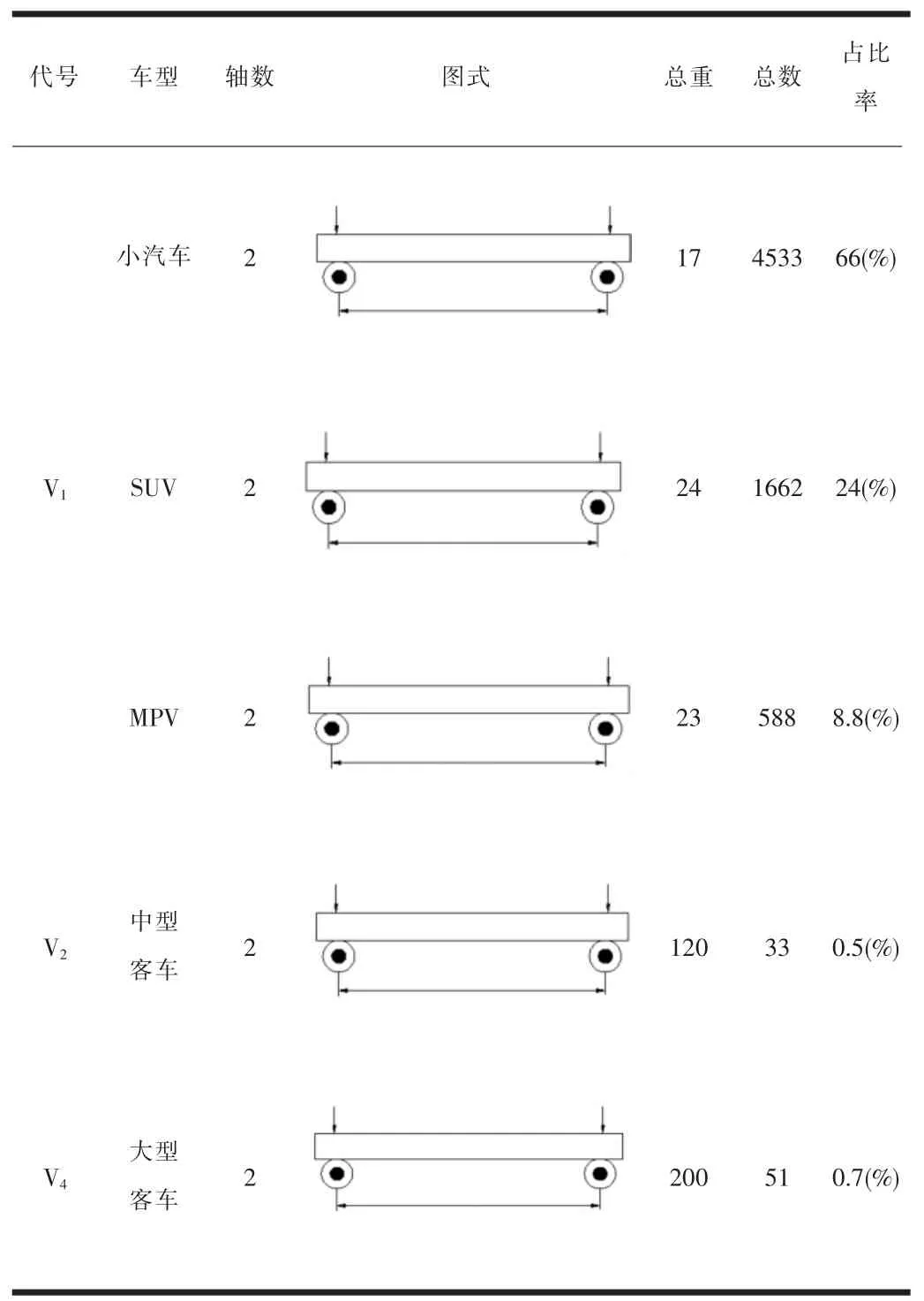
表2 不同车型结构参数及频数

交通荷载调查数据经整理和分类后可作为原始荷载谱，但不能直接用于结构疲劳分析，需要将相同或相近的车辆荷载合并为对应的等效车型，由此得到的典型车辆荷载谱简洁实用。本文分别将普通小汽车、SUV和MPV具体车型进行合并以及中型客车、大型客车合并，按照疲劳损伤等效原则求出车型的等效轴重及车型的等效轴距，计算公式如下：

式中：m为疲劳方程S-N反斜率，本文取3；Wej为等效车型第i车轴的等效轴重；fi为同一类车中第i种车辆出现的频率；Wij为第i种车辆第j轴的轴重；Aj为等效车型第j个轴距；Aij为第i种车辆的第j个轴距。

由此得到两类典型的V1和V2疲劳车辆，其结构参数见表3。

表3 疲劳车结构参数

2 标准疲劳车模型推导原理

推导的标准疲劳车辆应等效于实际车辆运营时对构件造成的损伤[8]。根据车辆统计数据，对各轴车在实测数量作用下的结构疲劳累积损伤进行分析，找出对疲劳累积损伤贡献最大的车型，为标准疲劳车的推导提供车型依据。损伤累积与常幅应力幅相关，常幅应力幅通过变幅应力幅推算而来[9]。Palmgren-Miner“线性积伤律”准则认为变幅疲劳中各个应力幅△σi所造成的损伤可由ni/Ni来定量表示，且可以线性叠加。因此，对任意构件在变幅应力循环作用下的损伤度可定义为：

构造细部的常幅疲劳方程为：

mlg△σ+lgN=lgC （4）

由此可得该构造细部在△σi、ni（i＝1、2、3…）重复荷载作用下的损伤度为：

根据损伤度等效原则，可以得出等效应力幅：

根据所得到的车辆荷载频值谱，将疲劳荷载谱中的每一辆典型车通过典型跨径的简支梁以及本文的实桥计算出跨中弯矩的历程，采用式（7）求出等效弯矩幅。

通过泄水法求出等效弯矩的作用循环次数，并按式（8）找出损伤度占比大的典型车辆，并将其定为标准疲劳车。

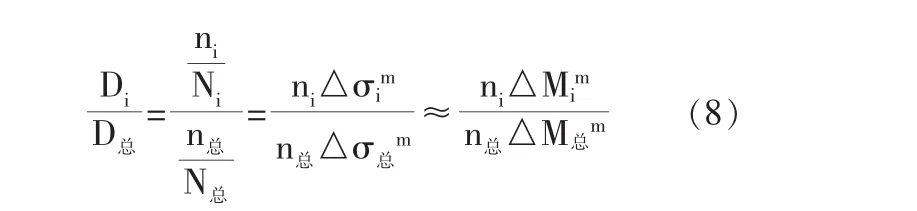
式中：△σi为i轴车的应力幅值，参数m借鉴AASHTO关于疲劳的细节规定[10]，统一取为3。

3 一般运行状态下的标准疲劳车模型

3.1 简支梁加载

将V1和V2疲劳车辆加载到跨径1.2～100m的简支梁计算产生的跨中弯矩内力历程。由于篇幅限制，本文只给出了普通小汽车和客车在5m和10m简支梁的跨中弯矩内力历程图，如图2和图3所示。

图2 5m简支梁跨中弯矩历程图

图3 10m简支梁跨中弯矩历程图

由图2可知，当影响线长度在5m及以下时，车辆的每个轴都会产生一个内力幅。而当影响线长度超过10m后，每个模型车只产生一个内力幅。由内力历程借助泄水法计算内力幅，得到等效内力幅和循环次数。并按式（8）计算出在同一跨径下两类车型所造成的损伤占比，计算结果见表4。

表4 移动荷载下的标准疲劳车计算

由表4可知，当桥梁跨径在1.2～5m时，V1和V2的疲劳车模型等效损伤占比不变，分别为6.9%和92.1%。当桥梁跨径在10～50m时，V1疲劳车所造成的损伤占比随跨径在逐渐减小，减小幅度为10%，而V2疲劳车则增加。换言之，轴重大的V2疲劳车与轴距小的V1疲劳车所造成的损伤比值在增大。由此可说明在此跨径区间内，车辆轴重比轴距对损伤的贡献更显著。当桥梁跨径为50～100m时，虽然V1疲劳车的等效损伤占比还在逐渐减小，但幅度却非常小，为0.6%。这是因为跨径的增大削弱了车辆轴重对损伤的贡献。总的来说，V2疲劳车的等效损伤贡献率远远大于V1疲劳车。

3.2 等跨连续梁实桥加载

实桥全长90m，上部结构为30m+30m+30m三跨预应力先简支后连续T梁桥，每幅共四片T梁。

边跨预制部分翼缘宽为1.975m，中跨预支部分翼缘宽为1.7m，翼缘厚度为0.16m。跨中梁肋厚度为0.2m，在支点处逐渐变成0.5m。每跨共设置5道横隔板，T梁间的湿接缝宽为0.633m。采用Midas civil建立桥梁的有限元模型，共有364个节点和431个单元，如图4所示。

将两种典型疲劳车辆采用移动荷载形式加载到本文建立的3跨连续梁实桥模型，计算实桥跨中弯矩的内力历程，其计算过程如下：

图4 桥梁有限元模型

1）将典型疲劳车辆按最不利偏载车道位置加载到实桥上，由于只比较两类疲劳车对桥梁造成的损伤大小，因此采用单车道加载简化计算；

2）通过Midas civil计算提取出加载两侧的影响线值，如图5所示，并取两侧影响线的均值作为最终求解内力历程的影响线值；

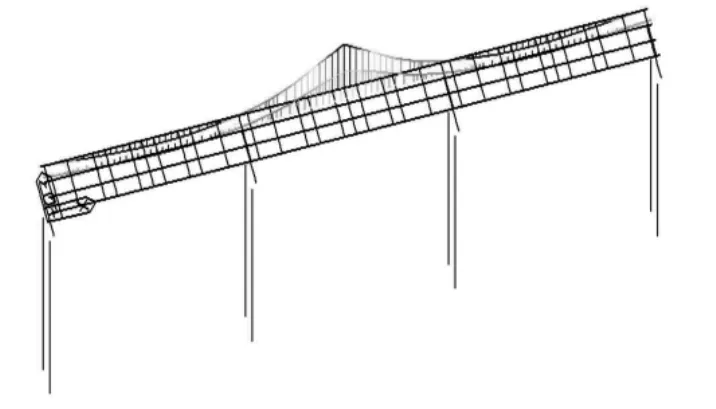
图5 实桥的影响线图

3）由于所提取出来的影响线值的坐标为模型中各单元横坐标，因此要通过线性插值的方法来求得车辆前后轴两个加载点处所分别对应的影响线值；

4）将前后轴重一一与自身对应加载点的影响线值相乘后再相加得到最终的内力历程。

通过上述计算后，以前轴位置为横坐标即可得到弯矩内力历程，如图6所示。

图6 实桥弯矩历程图

由图6采用泄水法计算可知，两类车型通过实桥会产生两个内力幅，其中V1疲劳车产生的内力幅值分别为59.9kN·m和10.6kN·m，V2疲劳车产生的内力幅值分别为495.4kN·m和93.8kN·m。带入式（7）得到等效内力幅和循环次数，并按式（8）计算出在同一跨径下两类车型所造成的损伤占比，计算结果见表5。由表5可知，V2疲劳车模型对到实桥上所造成损伤贡献率约为V1疲劳车模型的10倍。

表5 移动荷载下的标准疲劳车计算

综上分析可知，将两类疲劳车模型加载到1.2～100m简支梁以及本文等跨连续梁实桥上，计算得到V2疲劳模型对桥梁所造成的损伤占比基本在90%及以上。说明了V1疲劳模型由于其轴重太小而对桥梁所造成的疲劳损伤很小，印证了英国规范中认为小于30kN的营业车产生的桥梁疲劳损伤很小的结论。因此本文将V2疲劳车模型作为城市桥梁的标准疲劳车模型（下文简称为标疲车A），其总重为公路桥梁的标准疲劳车模型的30%～50%。因此在进行城市桥梁设计时（尤其是城市中心限制货车等重车通行处的桥梁），若采用现有规范中的标准疲劳车模型，则使桥梁的疲劳设计安全系数富余过大而造成不必要的经济损失。

4 拥堵状态下的标准疲劳车模型

上一节研究了车辆一般运行状态下的城市桥梁标准疲劳车模型，由于所研究的城市桥梁发生怠速拥堵的频次非常高，因此应考虑研究此类桥梁在车辆拥堵状态下的标准疲劳车模型。研究基本方法为将每一次拥堵车列整体作为一次对桥梁的疲劳加载，发生拥堵的频次作为对桥梁的疲劳加载次数。如若将拥堵车列直接作为拥堵状态下的疲劳车模型，因为其轴数过多且各轴重偏小而不利于反映出拥堵状态下车辆对桥梁造成的疲劳损伤，因此可将拥堵车列按总重不变的原则近似化等效为一辆标准车以减少轴数并增加单个轴重。

频繁发生的拥堵工况是建立拥堵条件下疲劳车模型的基本前提。为此对所采集到的拥堵照片进行筛选和整理后，选取了两种发生频繁的疲劳拥堵工况：

1）全部由小汽车构成的疲劳拥堵工况M1，车列长度为50m，其排布如图7所示。

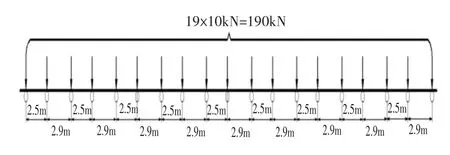
图7 M1车列布置图

2）由小汽车加上一辆大型客车构成的疲劳拥堵工况M2，车列长度为50m，其排布如图8所示。

图8 M2车列布置图

拥堵工况M1和拥堵工况M2的总重分别为190kN和360kN，按照总重不变的原则进行近似等效的关键在于确定轴数。标疲车的轴数一般为2～6轴，5～6轴的标疲车适用于载重货车通行频繁等特定区域公路桥梁上，故本文不适宜采用5轴或者6轴的标疲车。2～4轴标疲车适用于一般的公路和城市桥梁，由于拥堵车列的总长度为50m，若采用2轴车则会导致轴距太大不适宜作为疲劳车。故本文根据两种拥堵工况的排列状况以及轴重分布，最终将M1和M2拥堵车列分别等效为3轴和4轴疲劳车。等效的具体过程如下：

（1） M1拥堵工况

将车列中排列的19个小汽车轴重分为三组，两组为60kN，一组为70kN。并取每组中6个或者7个轴重加载点的中间位置为新的等效轴重加载点。由此将M1拥堵工况的车列等效为一辆3轴车疲劳车，其等效过程如图9所示，各轴重与轴距见表6。

图9 等效3轴车示意图

表6 3轴车与4轴车的构造参数

（2） M2拥堵工况

拥堵车列中客车的两个轴重都为100kN，可保留其轴重和轴距不变。将其余的16个小汽车轴重分为两组，每组的总重为80kN，并且取每组中8个轴重加载点的中间位置为新的等效轴重加载点。由此将M2拥堵工况的车列等效为一辆4轴疲劳车车，其等效过程如图10所示，各轴重与轴距见表6。

图10 等效4轴车示意图

将以上两类典型拥堵状态下的疲劳车加载到等跨连续梁实桥计算其跨中弯矩内力历程，计算过程同一般状态下疲劳车辆的推导，结果如图11所示。

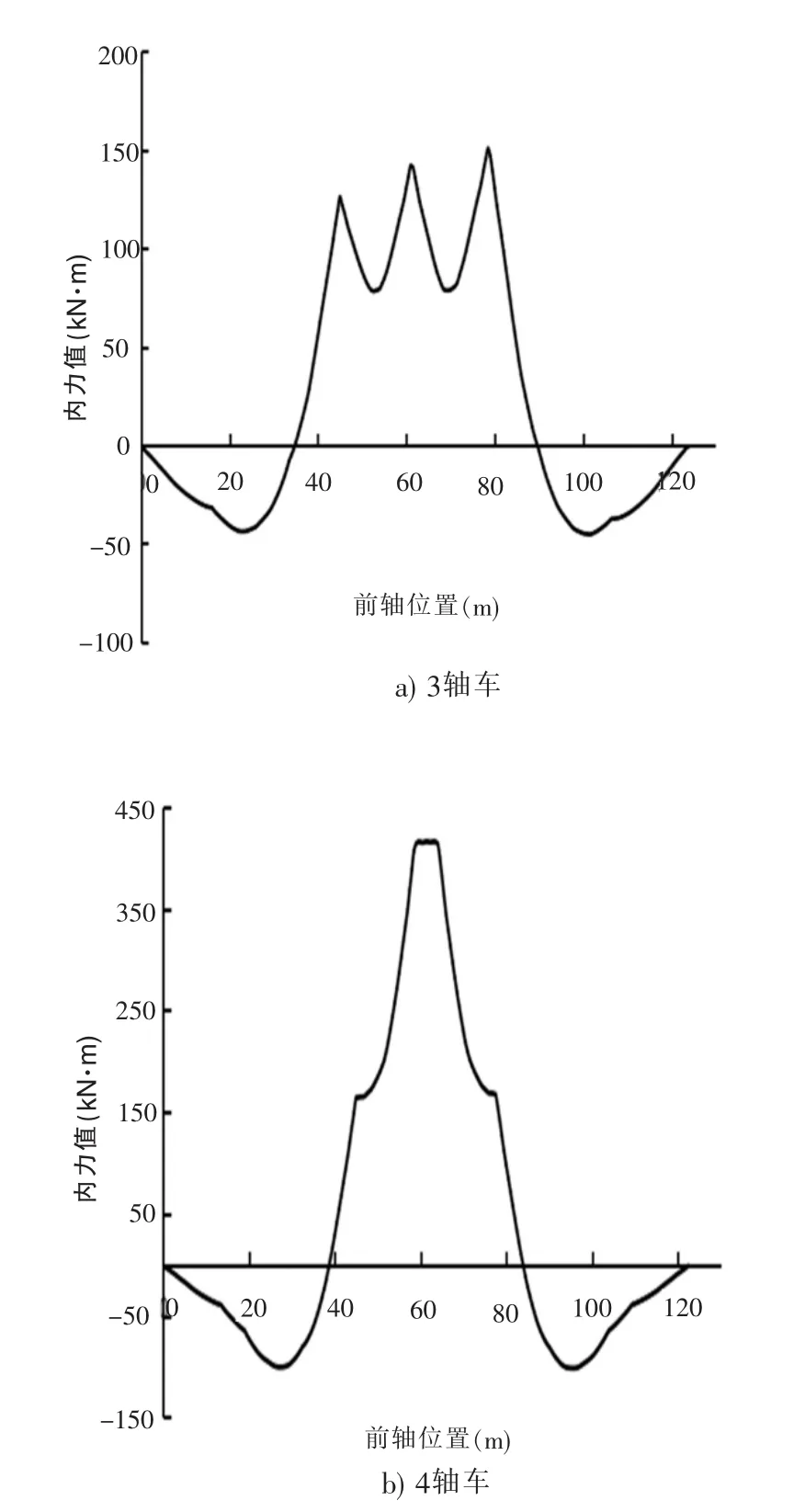
图11 实桥弯矩历程图

由图11采用泄水法计算可知，拥堵状态下3轴和4轴疲劳车模型通过实桥分别会产生4个和2个内力幅，按式（7）计算可得到等效内力幅和循环次数，并按式（8）计算出在同一跨径下两类车型所造成的损伤占比，计算结果见表7。

表7 两类车型对实桥造成的损伤占比

由表7可知，4轴疲劳车模型加载到实桥上所造成损伤贡献率为72%，明显大于3轴疲劳车。因此本文将等效4轴疲劳车作为拥堵状态下的城市桥梁标准疲劳车模型（下文简称为标疲车B）。

5 标疲车模型比较

本节将对一般运行和拥堵状态下的标准疲劳车模型A、B，BS5400、AASHTO提出的标准疲劳车模型，以及西南山区高速的标疲车[12]（标准疲劳车C）和渝湛高速的标疲车[13]（标准疲劳车D），在简支梁上产生的损伤进行比较，各标疲车形式汇总见表8。

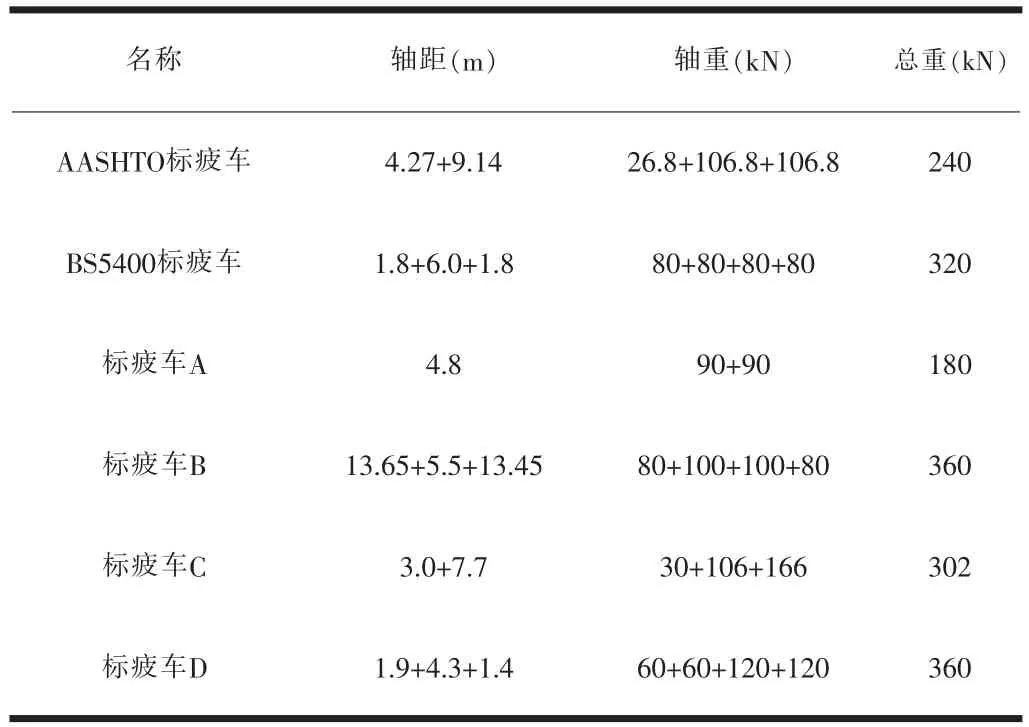
表8 不同标准疲劳车模型

将各疲劳车模型通过1.2～50m跨径的简支梁，并按式（7）计算在简支梁跨中产生的等效弯矩幅，计算结果如图12和图13所示。

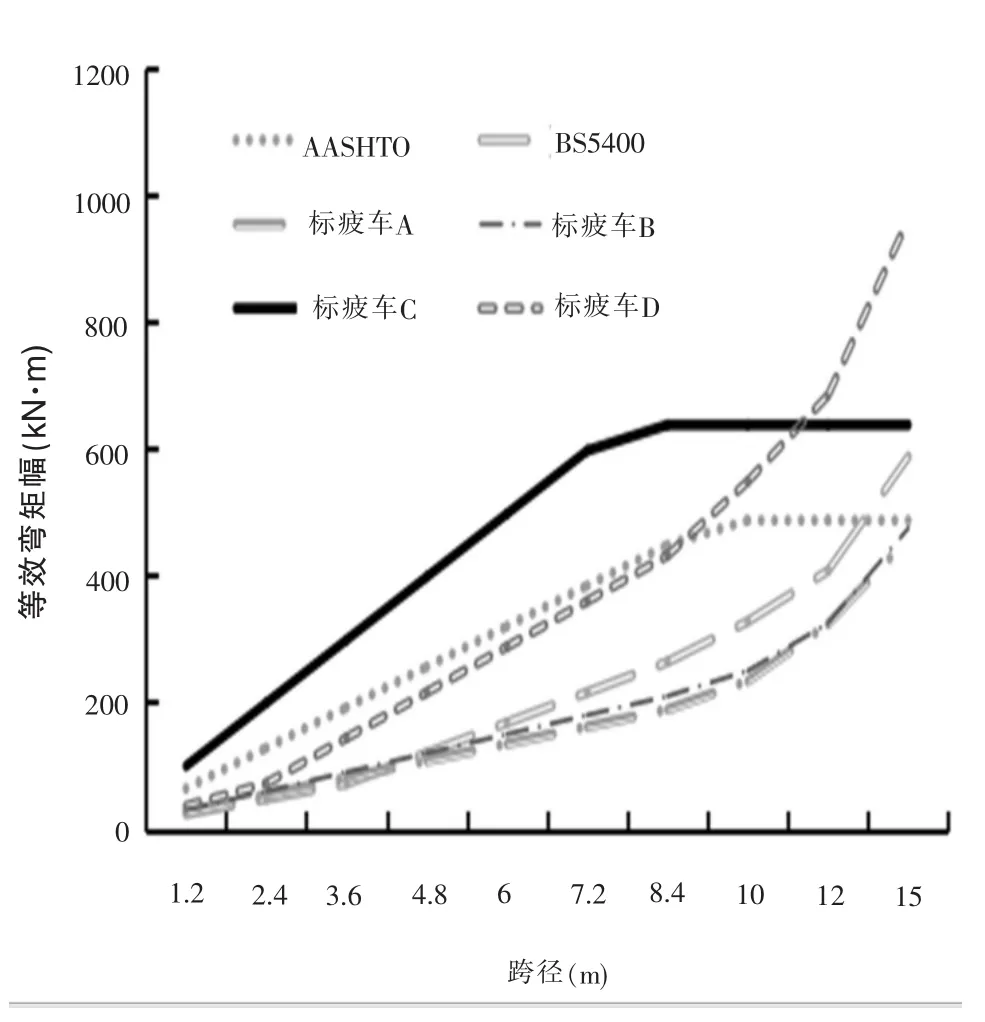
图12 1.2～15m简支梁跨中弯矩

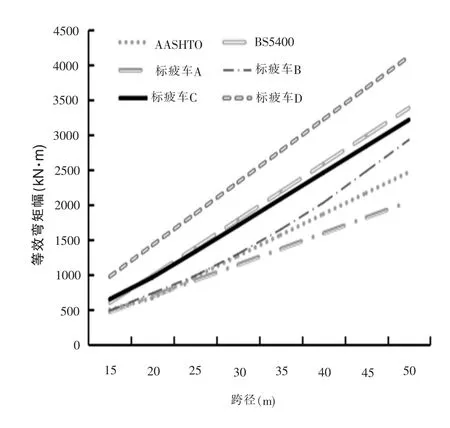
图13 15～50m简支梁跨中弯矩

当桥梁跨径在15～50m时，产生弯矩内力幅从大至小依次为标疲车D、BS5400标疲车、标疲车C、AASHTO标疲车和标疲车A（不考虑标疲车B）。由此说明一般运行状态下的标疲车总重越大，产生的内力幅则越大。拥堵状态下标疲车B则不遵循此规律，其轴距已经远远大于正常运营车辆。而当桥梁跨径为1.2～15m时，各标疲车产生的弯矩内力幅大小并没有与轴重、轴距或总重等单一变量呈现出明显递增或者递减的规律。

当桥梁跨径为1.2～15m时，本文的标准疲劳车A、B模型产生的内力幅很接近但均小于BS5400标疲模型。当桥梁跨径在15～50m时，标准疲劳车A、B模型产生的内力幅分别稍大和稍小于AASHTO标疲车模型。然而不论桥梁跨径为多大时，标疲车C、D模型产生的内力幅都明显大于标疲车模型A、B，因此公路桥梁的标准疲劳车并不适用于城市桥梁。

当桥梁跨径为1.2～30m时，一般状态的标疲车A与拥堵状态下的标疲车B产生的内力幅相差为3%～12%，较为接近。而当桥梁跨径为30～50m时，二者相差为12%～30%。由此可见标疲车A和标疲车B产生的内力幅的差值，随着跨径的增大而增大。在进行疲劳设计时，可根据跨径选择一般状态或拥堵状态下的标疲车模型。