基于改进萤火虫算法的LSSVM脉动风速预测
2019-01-23郑晓芬
郑晓芬 徐 畅
(同济大学土木工程学院,上海 200092)
0 引 言
风作为一种荷载,同时也是一种能量的载体。当它出现在工程结构(尤其是超高层建筑)时,就对结构物的抗风设计提出了要求。在强风的作用下,结构物如果抗风设计不合理,就会产生较大变形甚至破坏[1]。而当风出现在风电场时,就对风电场的电力系统提出要求。如果风速过大,风电穿透功率超过一定比例之后,会严重影响电能质量和电力系统的运行[2-3]。对于风速如果能有一个较好的预测,在未来,对于超高层建筑将有更为安全可靠、经济合理的设计[4],对于电力系统也可以使电力调度部门必要时提前调整调度计划,有效地减轻风对电网的影响,而且还有其他诸多方面的意义。比如当风演变成为自然灾害时,对风速的预测将使我们提前做好面对灾害的准备,以将人员伤亡以及经济损失降到最低。因此,风速的预测应用前景广阔,研究收益极大,是值得不断努力、不断深入的研究方向。
随着近几十年来对人工智能研究领域的不断探索,人工智能已被广泛的应用并解决许多复杂的土木工程问题。最小二乘支持向量机[5](Least Squares Support Vector Machine,LSSVM)作为一种新颖的人工智能技术已被应用于土木工程领域中的风速预测。由于参数的选择对LSSVM的性能有极大的影响,经过发展,现通常与各种智能优化算法相结合,以减少参数对其性能的影响。而新兴的萤火虫算法(Firefly Algorithm,FA)具有设置参数少、易实现、收敛精度高等优点,但同时存在对优秀个体依赖程度高,易产生震荡现象的缺点。
为此,本文提出一种基于改进萤火虫算法优化最小二乘支持向量机风速预测模型,针对萤火虫算法的不足进行改进,并与基本萤火虫算法最小二乘支持向量机(FA-LSSVM)、粒子群加速优化最小二乘支持向量机(PSO-LSSVM)风速预测模型进行结果比对,评价改进萤火虫算法优化最小二乘支持向量机预测模型性能。
1 最小二乘支持向量机
支持向量机经过发展,现在已发展出最小二乘支持向量机。LSSVM是在SVM的基础上,采用误差的二次平方项代替SVM中的不敏感损失函数,将不等式约束改成等式约束,把二次规划问题转化为求解线性方程组问题,以提高求解速度和收敛精度,并成功地应用于函数逼近、分类以及时间序列预测等方面。其原理如下:
对于一个给定的训练集{(xi,yi)|i=1,2,…,n},xi∈Rn为n维输入数据,yi∈Rn为一维输出数据。φ(·)通过非线性映射函数将输入从原空间Rn映射到特征空间φ(·),将原输入空间中的非线性回归问题转化为高维特征空间中的线性回归问题,即
f(x)=ωTφ(x)+b
(1)
式中:φ(x)为映射函数;ω=[ω1,…,ωn]为权向量;b为偏置。
根据结构风险最小化原理,此线性回归问题可表示为一个等式约束优化问题。LSSVM目标函数为
(2)
s.t.yi=ωTφ(xi)+b+ei(i=1,…,n)
(3)
式中:J为损失函数;γ为正则化参数且γ>0;ei为误差变量。
将约束优化问题转化为无约束优化问题的拉格朗日等式为
(4)
式中,αi(i=1,2,…,n)为拉格朗日乘子。
将L分别对ω,b,ei,αi求偏导数,并令等于0得方程:
(5)
令1n=[1,1,…,1],∝=[∝1,∝2,…,∝n],Ωn=[y1,y2,…,yn]T,Y=[y1,y2,…,yn]T,I为单位矩阵,联立方程组消去ω,ei,式(5)简化为
(6)
由式(6)求出α和b,得到LSSVM回归模型:
(7)
式中,k(x,xi)为核函数,它是解决非线性分类、回归问题的关键,通过核函数将非线性问题映射到高维特征空间,在这个空间内便可进行线性划分。
2 基本人工萤火虫算法
萤火虫算法是由剑桥大学Yang[6]在2008年提出的一种新颖的仿生智能优化算法,通过模拟萤火虫觅食、择偶等习性而产生的相互因发光吸引而移动的行为来解决最优问题。萤火虫算法是基于以下三个理想化特征提出的:①萤火虫不分性别,即萤火虫之间的相互吸引力只考虑个体发光的亮度;②吸引力与发光亮度成正比,与个体之间的距离成反比;③萤火虫的亮度由待优化的目标函数值决定,即Ii=f(xi)。
在FA中,萤火虫彼此吸引的原因取决于两个要素,即自身亮度和吸引度。亮度小的萤火虫被亮度大的萤火虫吸引而向其移动,并更新自身位置。萤火虫的发光亮度取决于自身所处位置的目标值,亮度越高所表示的目标值越好,吸引其他萤火虫的能力也越强。若发光亮度相同,则萤火虫各自随机移动。算法的数学描述与分析如下:
定义1 萤火虫的相对荧光亮度:
(8)

定义2 萤火虫的吸引度:
(9)
式中,β0为最大吸引度,即r=0处吸引度。
定义3 萤火虫i被吸引向萤火虫j移动的位置更新公式:
xi=xi+β×(xj-xi)+α×(rand-0.5)
(10)
式中:α为步长因子,是[0,1]上的常数;rand为[0,1]上服从均匀分布的随机数。
算法流程如图1所示。
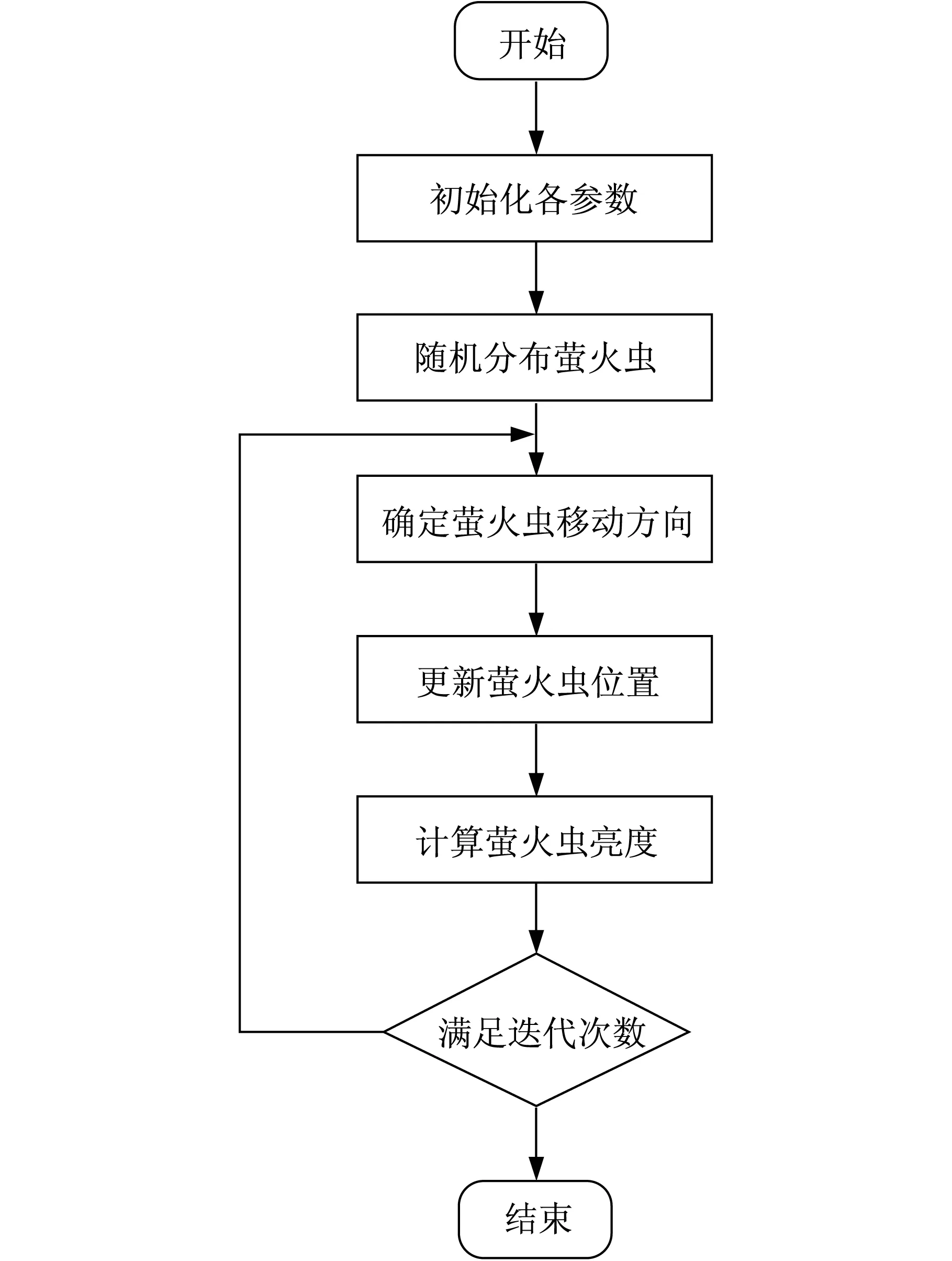
图1 人工萤火虫算法流程Fig.1 Algorithm flow of artificial firefly
3 萤火虫改进算法
由式(10)可以看出,当个体距离峰值非常近时,由于步长可能大于该距离,将导致个体在峰值附近发生震荡现象。因此步长的设定很关键。通过多次实验发现,当α取值较大时能够较好实现全局寻优,但在算法后期不易收敛,当取值较小时虽提高了收敛效果,却易于陷入局部最优[7]。本文考虑,在迭代过程中加入一种自适应步长,当某一个体被另一个体吸引时,如果两者空间距离大于步长,则仍采用初始步长进行移动,如果两者距离小于步长,则步长调整为0.9倍的空间距离,带入位置更新公式中。这样,在最优解附近搜索时,既能保证搜索范围的覆盖,又能避免在最优解附近发生震荡现象。其伪代码如下:
ifrij>步长
步长=0.9*rij
else
步长=初始步长
end
为了加强萤火虫之间的吸引,在距离较远时仍能产生一定的相互移动,改进萤火虫的吸引度公式:
β=(β0-βmin)e-γrij+βmin
(11)
式中:β0为最大吸引度,即r=0处吸引度;βmin为最小吸引度。
在传统萤火虫算法中,每一代最优个体没有作相应处理,导致最优个体进化停滞,不利于算法的进一步收敛。采用文献[8]中高斯算子对最优个体进行变异,给每次迭代得到的最优个体加上一个服从高斯分布的随机扰动项,如下:
xGbest=xbest+xbestN(0,1)
(12)
式中:xbest为当前最优萤火虫;xGbest为变异后的最优萤火虫;N(0,1)为均值为0、方差为1 的高斯分布随机变量。
最后比较变异前后萤火虫适应度值的大小,取两者中适应度值较佳的个体为本次迭代的萤火虫最优个体xbest。
4 实验结果与分析
本次实验数据采用30 m高度处建筑物实测风速1 000个(采样频率为1 Hz,平均风速为-0.78 m/s,附近建筑相距较远),取前800个作为训练集,后200个为测试集,嵌入维数m=10。基本萤火虫算法与改进萤火虫算法中萤火虫数m=30、最大吸引度β0=1.0、最小吸引度βmin=0.25,光强吸收系数γ=1.0、步长因子α=0.25、最大迭代次数Max=150。粒子群加速算法中最大迭代次数Max=150,种群规模m=30,k=0.5。LSSVM参数σ∈[0.1,1 000],γ∈[0.1,1 000]。实验平台为MATLAB,版本为2012b。实验结果如图2-图4所示。
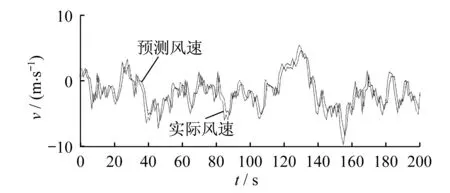
图2 改进FA算法预测风速与实测风速的幅值对比Fig.2 Amplitude comparison between wind speed predicted by improved FA algorithm and measured wind speed
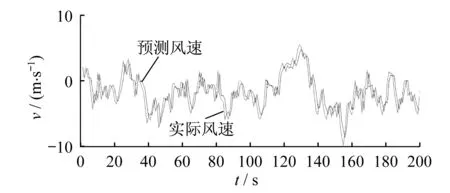
图3 基本FA算法预测风速与实测风速的幅值对比Fig.3 Amplitude comparison between wind speed predicted by basic FA algorithm and measured wind speed
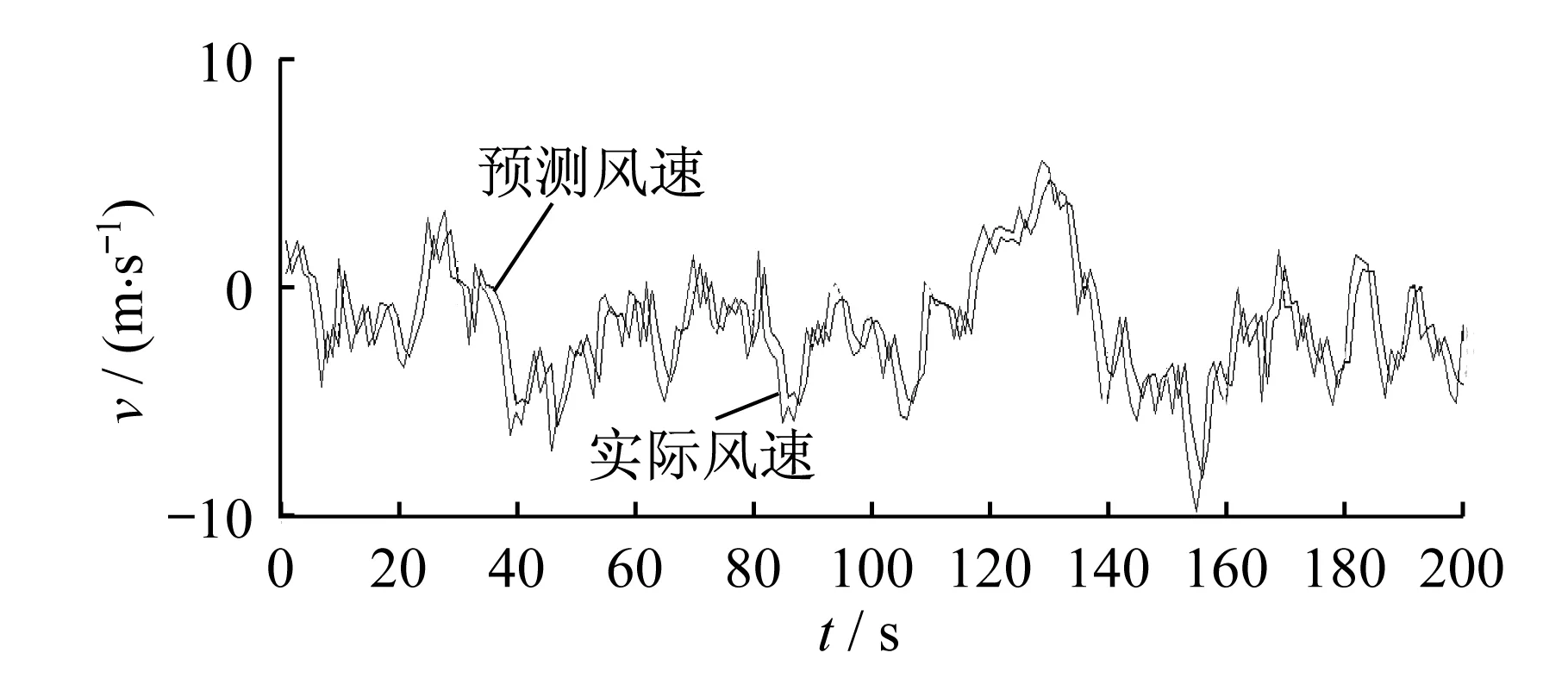
图4 粒子群加速算法预测风速与实测风速的幅值对比Fig.4 Amplitude comparison between wind speed predicted by Particle swarm acceleration algorithm and measured wind speed
由图5可知,改进萤火虫算法优化的LSSVM风速预测模型在精度和收敛速度上都大于基本萤火虫算法和粒子群算法优化的LSSVM风速预测模型。改进萤火虫算法在迭代10次左右就达到算法最优值,粒子群算法在迭代20次左右达到算法最优值,基本萤火虫算法在迭代80次左右达到最优值。但在本次实验中,由于算法本身对初始个体的依赖性较大,因此在实验中并不能保证每次运算都能达到较好的实验精度,多次实验的结果离散性较大,而此结果是在对萤火虫算法及改进萤火虫算法进行多次实验取其最优结果而成。因此,萤火虫算法对初始优秀个体的依赖将极大地影响实验结果。
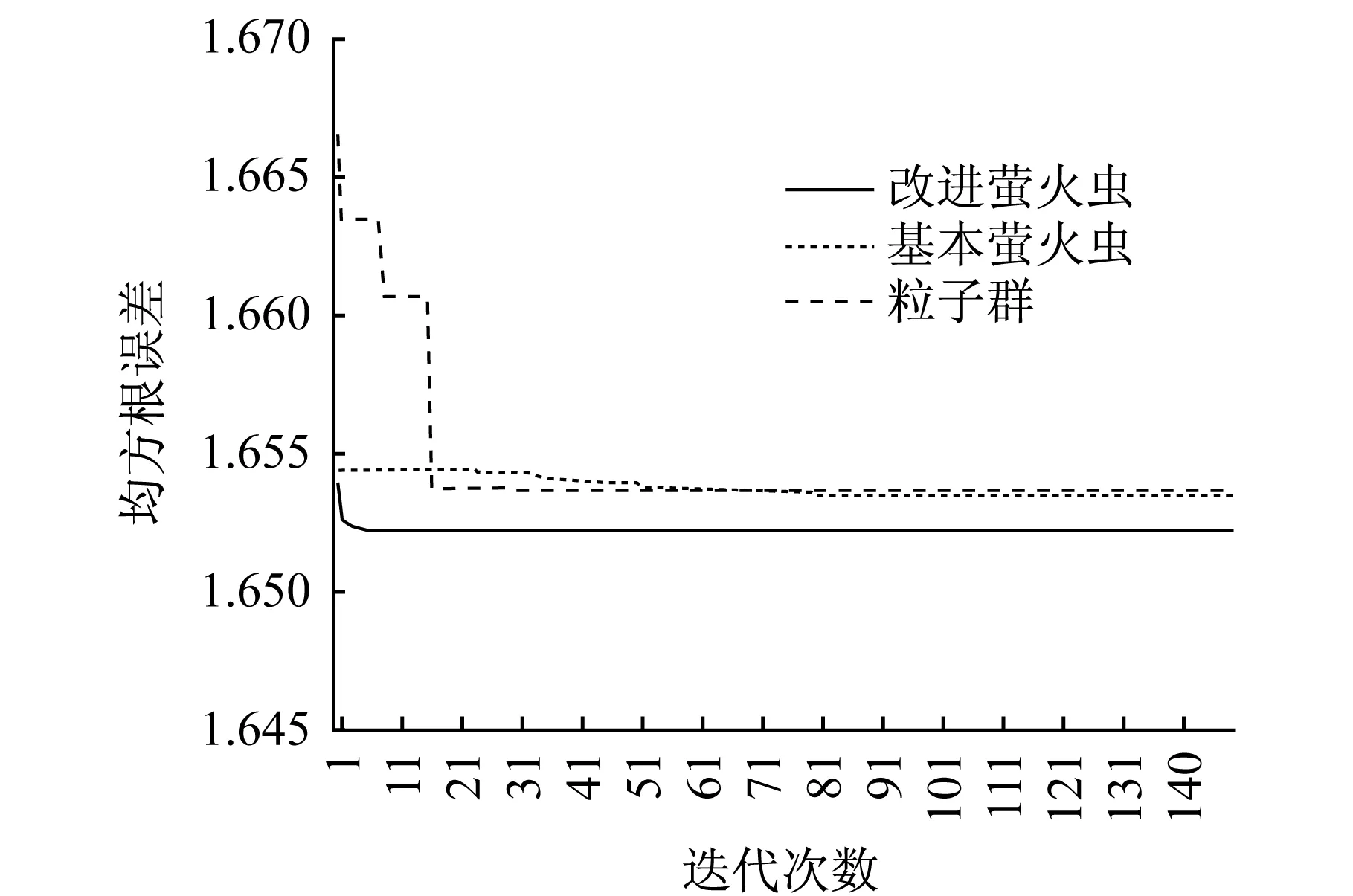
图5 三种预测模型的收敛速度Fig.5 Convergence rate of three prediction models
5 结 论
(1) 本文通过对萤火虫算法进行改进,并结合LSSVM建立风速预测模型,实验表明,改进的萤火虫算法在预测精度与收敛速度方面较基本萤火虫算法和粒子群算法都有更好的效果,有一定实际应用价值。
(2) 实验也暴露了算法的不足,即萤火虫算法对初始优秀个体的依赖程度较高,下一步将针对这个问题再加以改进研究。
