一种基于多点峭度谱和最大相关峭度解卷积的滚动轴承故障诊断方法

2019-01-23刘文朋廖英英杨绍普刘永强顾晓辉

振动与冲击 2019年2期

刘文朋，廖英英，杨绍普，刘永强，顾晓辉

(1. 石家庄铁道大学机械工程学院，石家庄 050043； 2. 石家庄铁道大学土木工程学院，石家庄 050043)

滚动轴承的运行状态监测和故障诊断一直是旋转机械健康维护的重要组成部分[1]，目前，滚动轴承故障诊断研究方法多种多样，技术也日益成熟，其中，基于解卷积的方法逐渐引起了广泛的关注。

最小熵解卷积(Minimum Entropy Deconvolution，MED)方法可以对振动信号进行盲解卷积，从而消除传递路径的影响，突出信号中的冲击信息[2-3]，文献[4]首先将MED算法应用到滚动轴承的故障诊断领域，并取得了良好的效果。文献[5]将MED与谱峭度(Spectral Kurtosis，SK)相结合成功应用于滚动轴承循环冲击特征的增强，文献[6]将MED与稀疏分解相结合应用于强背景噪声下的滚动轴承微弱故障特征提取，均受到了广泛的关注。然而，也有研究发现MED方法存在一定的缺陷，通过解卷积输出的结果，常常会出现只突出单个脉冲或一些与故障冲击无关的脉冲成分。为此，文献[7]在MED算法的基础上提出了一种最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution, MCKD)的方法，旨在通过解卷积输出与故障相关的周期性脉冲成分。近几年，MCKD作为一种增强信号中的周期性冲击成分的有效算法，被广泛用于滚动轴承的故障诊断中[8-10]。然而，MCKD算法对参数的要求极为严格，只有当解卷周期与相应的故障周期相匹配时，MCKD算法才能发挥最优的效果[11]。在滚动轴承参数已知的前提下，尽管可以通过理论计算得到故障周期，但是需要获得准确的转速信息。此外，由于转速波动等随机因素的影响，测量转速与实际转速往往会存在一定的误差，导致计算的故障周期与实际的故障周期产生差异，从而影响了MCKD算法的有效性。因此，获得准确的周期T是进行MCKD算法的必要的前提。

为了克服MCKD需要预知准确的故障周期的缺点，更好的增强感兴趣的故障冲击成分，提出了一种基于多点峭度谱[12]和MCKD的滚动轴承故障诊断方法。该算法通过对比不同周期下解卷积结果输出的信号的多点峭度，检测处于不同周期下信号的强度，从而寻找出滚动轴承典型故障周期的准确取值，对预先估计的故障周期进行修正，将得到的故障周期输入到MCKD算法中，增强原信号中周期性故障冲击成分，最后通过包络解调来进行诊断故障。通过仿真信号和实验信号分析，证明了该方法的有效性。

1 诊断方法的基本原理

1.1 多点优化最小熵解卷积(MOMEDA)原理

为了提取信号中的周期性故障特征，最大相关峭度解卷积方法通过选取一个有限冲击响应滤波器通过循环迭代使周期已知信号滤波后的相关峭度最大，从而达到突出信号中的冲击成分的目的，而MOMEDA(Multipoint Optimal Minimum Entropy Deconvolution Adjusted)算法将一个无限长的脉冲序列作为输出目标，可以直接寻找出最优的滤波器参数，而非迭代的方式。MOMEDA算法中优化的目标函数为

(1)

(2)

MOMEDA滤波参数和输出结果可以简化为

(3)

(4)

(5)

tn=Pn(T)=δround(T)=δround(2T)+

(6)

(7)

(8)

(9)

(10)

对于不同周期T下解卷积下输出的信号，可以通过多点峭度指标(Multipoint Kurtosis)来衡量故障成分大小。

(11)

多点峭度谱可以通过计算采样信号中不同周期下的解卷积输出信号的多点峭度值，显示出信号中含有的周期性成分的对应的周期和强度，当信号中存在由滚动轴承故障引起的故障冲击时，多点峭度谱中对应的故障周期、整数倍周期和分数倍周期处的谱峰将会明显高出其他位置，据此可以定位故障周期的准确取值。

1.2 MCKD算法

MCKD算法中相关峭度的定义为

(12)

式中：T为感兴趣故障冲击的周期；N为采样点数；M为位移数，表示卷解积的脉冲序列，M值越大，解卷积脉冲序列越高。

MCKD算法中优化的目标函数为

(13)

(14)

r=[0T2TmT]

(15)

(16)

(17)

MCKD算法迭代寻找f过程如下：

步骤1选择滤波器L、周期T和位移数M，迭代次数N；

步骤3计算滤波后的输出信号y(n)；

步骤4根据y(n)计算Am与B；

步骤5更新滤波器的系数f；

步骤6如果滤波前与滤波后信号的ΔCKM(T)小于给定阈值，则停止递归，否则回到步骤3。

MCKD算法解卷积时需要输入故障周期T，故障周期的准确性将对故障诊断效果带来影响，对故障冲击信号周期估计误差越大，解卷积效果越差，而实际工程应用中的故障频率的估计往往很难非常准确[13]，从而使得MCKD算法中T与实际情况不符，导致算法失效。

2 基于多点峭度谱和MCKD的滚动轴承故障诊断方法

多点峭度谱和MCKD相结合的滚动轴承故障诊断方法流程，如图1所示。首先根据被检对象的结构参数和预估计的转速计算出所有的故障特征频率，然后根据故障频率和采样频率计算出相应的故障周期，通用多点峭度谱算法对振动信号进行处理，通过比较不同周期下解卷积结果输出的信号的多点峭度谱，对预先估计的故障周期进行修正，获得准确的故障周期T,再把周期T输入到MCKD算法中，最后通过包络解调进行故障诊断。

此外，该算法还可以用于复合故障的诊断，当信号中存在复合故障时，可以将通过多点峭度谱获得的滚动轴承不同部位故障周期依次输入到MCKD算法中，利用故障出现的周期信息，实现复合故障信号的分离提取，而后对各分量进行包络解调，从而实现复合故障的诊断。

为了方便研究，本文选用周期T对应的采样点数(采样周期Ts)作为输入的故障周期，采样周期Ts定义为

Ts=fs·T

(18)

式中：fs为采样频率；T为感兴趣故障周期。

图1 新方法流程图Fig.1 Flowchart of the new method

3 仿真信号分析

3.1 仿真信号

仿真信号由冲击信号、噪声信号和谐波信号3部分构成，可得滚动轴承单点损伤振动模型，其表达式为

x1=e-αtAsin(2πf1t)

(19)

(20)

x3=Csin(2πf2t)

(21)

y=x1+x2+x3

(22)

式中：α=800为衰减率；A=0.8为冲击幅值；t为时间；f1为冲击引起的共振频率；B=3.6为噪声幅值；z为随机数；C=1.0为谐波幅值；f2为谐波频率。

3.2 分析与验证

设置共振频率f1为3 kHz，转频f2为25 Hz，冲击信号的频率fo为64 Hz，采样频率fs为10 240 Hz，采样时间为1 s，则对应的采样周期的理论计算值为160，仿真信号的时域图如图2所示。假设在进行分析前未知准确的故障周期，预估计故障采样周期为165，与实际值存在一定偏差。

选择Ts=165，对原信号进行MCKD滤波后进行包络解调分析，包络谱如图3所示，在图中故障特征频率及其倍频处看不到明显的峰值，未能诊断出仿真信号中存在的故障冲击成分，说明了MCKD算法对故障周期的准确性要求极为严格，周期选择不当可能会导致算法的失效。

图2 仿真信号时域图Fig.2 The time domain of simulation signal

图3 MCKD降噪信号包络谱(Ts=165)Fig.3 The envelope spectrum after MCKD(Ts=165)

采用多点峭度谱对仿真信号进行处理，周期范围选取[10,360]，窗函数选择为[1, 1, 1]，周期谱如图4所示，可以看出在预估计采样周期165局部范围内，Ts=160处谱峰具有明显较高的幅值，所以可以初步断定其为故障周期，当选择采样周期Ts为160时，与之对应的半周期1/2Ts=80，一倍半周期3/2Ts=240，二倍周期2Ts=320处的峰值均比较突出，进一步说明了Ts=160为可能存在的故障采样周期。通过多点峭度谱计算的选择结果与理论计算的实际采样周期160相吻合，从而实现了故障周期的精确定位，证明了多点峭度谱在检测不同周期下的故障冲击信息强度的准确性。

图4 仿真信号多点峭度谱Fig.4 The mkurt spectrum of simulation signal

选取Ts=160，对原信号进行MCKD处理，对滤波后的信号进行包络解调分析，结果如图5所示，可以观察到故障特征频率fo=64 Hz及其2fo～7fo处的峰值均较为突出。

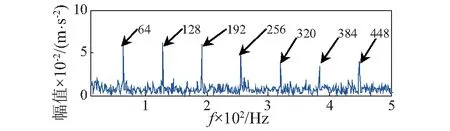
图5 MCKD降噪信号包络谱(Ts=160)Fig.5 The envelope spectrum after MCKD(Ts=160)

通过仿真信号的验证可知：在预估计的故障周期存在一定的偏差的条件下，MCKD算法将因无法获得准确的故障周期，从而无法用于故障特征提取，通过与多点峭度谱结合，克服了其限制。

4 实验信号分析

4.1 单一故障实验信号分析

为了验证本研究方法在滚动轴承故障特征提取中的有效性，在QPZZ-Ⅱ型旋转机械故障试验平台上进行分析，采用的轴承为6205-2RS型深沟球轴承，在轴承外圈上人为加工了一个直径为1 mm的圆点，模拟轴承表面损伤类故障，其主要参数见表1，轴承故障试验台如图6所示。

表1 试验轴承参数Tab.1 The parameters of test bearing

图6 QPZZ-Ⅱ型旋转机械故障试验台Fig.6 Fault simulation platform of QPZZ-Ⅱ type

试验时，振动加速度传感器安装在轴承座上，设置转速为1 500 r/min，转频为24.63 Hz，采样频率为25.6 kHz，选取10 240个数据点来进行分析，采样信号的时域图如图7所示。滚动轴承外圈故障频率为89.60 Hz，采样周期Ts的理论值对应为285.7。

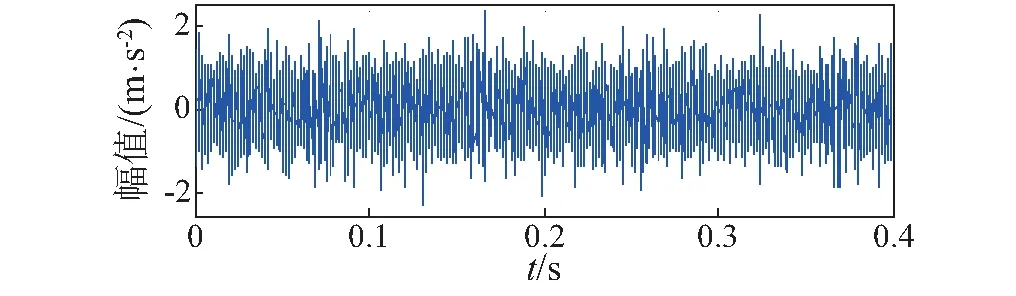
图7 原始信号时域图Fig.7 The original signal time domain

将采样周期Ts=285.7输入到MCKD算法中，滤波后的时域信号和包络谱如图8所示。图8(a)与图7相比，观察不到明显的的冲击成分；从图8(b)中仅可以观察到故障特征频率的3倍频，且干扰频率非常明显, 无法判断轴承是否发生故障。

通过多点峭度谱对采样信号进行运算，检测周期范围选择[20,600]，窗函数选择为[1, 1, 1, 1, 1]，结果如图 9 所示，从图中可以观察到在Ts=289.4处峰值较突出，与给定转速下的采样周期285.7接近，且当采样周期Ts选取289.4时，1/3Ts=96.5，1/2Ts=144.7，3/2Ts=434.2，2Ts=578.9处的峰值也比较突出，进一步验证了Ts=289.4为可能存在的故障周期。

图8 采样周期Ts=285.7Fig.8 Sampling period Ts=285.7

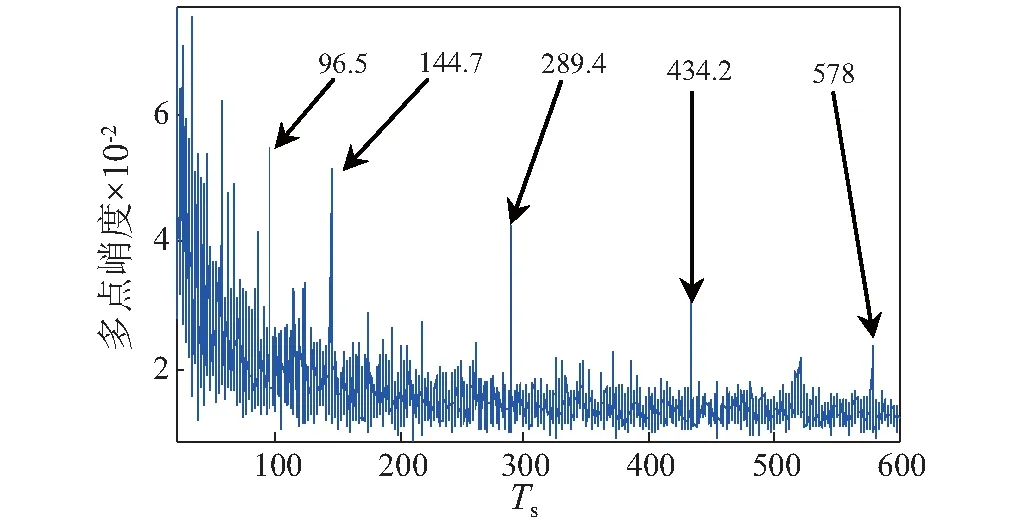
图9 实验信号多点峭度谱Fig.9 The mkurt spectrum of experiment signal

选取Ts=289.4，MCKD算法滤波后包络谱结果，如图10所示，可以观察到fo=88.25 Hz及2fo～4fo处的峰值均比较突出，可以判断外圈发生故障。

图10 MCKD降噪信号包络谱(Ts=289.4)Fig.10 The envelope spectrum after MCKD(Ts=289.4)

4.2 复合故障实验信号分析

以我国铁路60 t级货车使用的轮对轴承为研究对象，故障类型未知，实验所用铁路货车轮对跑合试验台，如图11所示。

将CA-YD-188型加速度传感器采样磁座安装在轴承座上，轮对转速设置为480 r/min，采样频率为12.8 kHz,轮对滚动轴承主要参数如表2所示，根据预先估计的转速，外圈、内圈、滚动体的理论故障特征频率依次为69.1 Hz，90.9 Hz，28.5 Hz。对应的采样周期依次为185.2，140.8，449.1。

图11 轮对跑合试验台Fig.11 Wheelset running test rig表2 轮对轴承主要结构参数Tab.2 The structure parameters of rolling bearings

轴承直径D/mm滚子直径d/mm接触角α/(°)滚子数目/列176.2924.748.83320

选取12 800个点来分析，原始信号时域图及包络谱如图12所示。从时域图中观察不到明显的冲击信息，包络谱图中可以发现没有特别突出的故障特征频率谱线，无法断定滚动轴承是否发生故障。

图12 原始信号时域图及其包络谱Fig.12 Original signal time domain and its envelope spectrum

将根据预估计转速下计算得到的内圈、外圈、滚动体的采样周期分别输入到MCKD算法中，滤波后的包络谱如图13所示，从图13(a)中可以观察到峰值频率67 Hz和135 Hz，与计算求得的外圈故障特征频率及其二倍频接近，而图13(b)、图13(c)中未发现内圈、滚动体的故障特征频率，所以判断轮对轴承仅外圈发生了故障。

通过多点峭度谱对原信号进行运算，检测周期范围选择[10,600]，窗函数选择为[1, 1, 1, 1, 1]结果如图 14 所示，可以观察到Ts=189.3处峰值较突出，与在给定转速下外圈故障对应的采样周期185.2接近，且当选取外圈故障采样周期Ts=189.3时，1/3Ts=63.1，1/2Ts=95，2Ts=378.6，3Ts=568处的峰值也比较突出，进一步验证了Ts=189.3为可能存在的外圈故障周期。此外，还可以观察到在内圈故障对应的采样周期140.8附近，Ts=145处峰值较突出，且还可以观察到与之对应的半周期1/2Ts=72.5处的峰值，进一步验证了Ts=145为可能存在的内圈故障周期。

图13 预估计故障周期条件下MCKD分离信号包络谱Fig.13 The separation signal envelope spectrum after MCKD with prior fault period

图14 实验信号多点峭度谱Fig.14 The mkurt spectrum of experiment signal

选取Ts outer=189.3和Ts inner=145，分别进行MCKD方法滤波，滤波后包络谱结果如图15所示，从图15(a)可以观察到外圈故障特征频率fo=67 Hz及2fo～7fo处的峰值均比较突出；从图15(b)可以观察到内圈故障特征频率fi=88 Hz及2fi～5fi处的峰值比较突出，可以判断外圈、内圈均发生了故障。

图15 MCKD分离信号包络谱Fig.15 The separation signal envelope spectrum

由于预估计转速计算的故障周期与实际的故障周期存在一定的偏差，选其作为MCKD算法的参数，仅寻找出了故障冲击信息更为明显的外圈故障，而内圈故障产生的振动信号由于传递路径更为复杂，导致采集到的故障冲击信息相对较弱，未能检测出内圈故障；通过多点峭度谱对故障周期的修正，不仅更好的突出了外圈故障的信息，观察到了外圈故障特征频率的1～7倍频，而且发现了预估计故障周期条件下未能检测出来的内圈故障，体现了新算法的优越性。