基于Warshall-Floyd算法的船舶结构噪声传递路径研究
2019-01-23向育佳季振林赵欣棠
向育佳,季振林,赵欣棠
(哈尔滨工程大学 动力与能源工程学院,哈尔滨 150001)
传递路径分析法(Transfer Path Analysis, TPA)需要借助试验求出噪声源与测点间的传递函数,对于船舶这样复杂的声振环境,难以找到合理的测点布置方案。统计能量分析(Statistical Entropy Analysis, SEA)提供了一种可靠的分析复杂声振环境的方法,随着计算机技术的发展,统计能量分析已经成为船舶中高频段声振预测的主流数值方法。
由于统计能量分析理论基于3个核心假设:能量均布(Energy Equipartition)、随机不相关激励(Rain-on-the-roof Excitation)及扩散场(Diffuse Field)[1],因而可以将连续结构按照振动模态相似的原则划分为一系列独立的子系统(Subsystem)[2-3],各子系统内部用统一的状态参数描述。严格意义上的统计能量分析必须以保守、弱耦合以及直接耦合为前提[4],各子系统之间以功率流的形式交换能量,并遵循能量守恒定律,即
(1)

(2)
式中:ω为分析频段上的中心频率;ηij为子系统i~j的耦合损耗因子;ηi,ηj为子系统i,j的自损耗因子;Ei/ni,Ej/ni分别为子系统i,j的模态能量。统计能量分析已经能够很好的计算噪声传递过程中任意两个子系统间的能量数量,基于SEA分析中子系统的概念,连续结构的无数条传递路径被压缩为有限个子系统间可供枚举的有限条路径。但是在众多路径中究竟哪几条是主要的噪声传递路径,还需要在SEA预测的声振环境基础上对数据进行深度分析,建立可供工程应用的范式。
1 传递路径分析方法及问题
为了进一步阐释声振问题中能量传递路径,学者们提出了两类研究思路。一类是Craik[6-9]提出的路径效率方法(Path Efficiency Method,PEM),Guasch等[10-12]在此基础上进行了细化和发展;另一类是Carcaterra[13-14]提出的统计熵方法(Statistical Entropy Method,SEM),随后Le Bot等[15-17]进一步完善了统计熵分析传递路径的理论及方法。
1.1 路径效率方法(PEM)
路径效率概念是基于无环单向路径(Single Path)的SEA模型提出的,如图1所示,n个子系统首尾相连构成单向路径。由于功率单向流动的假设,耦合损耗因子不再严格遵守能量互易原理,认为:ηij≠0,ηji=0,(j>i),则参照式(1)n子系统的能量平衡方程
(3)
式中:ηii=ηi+∑ηik为子系统i的总损耗因子。由式(3)代换可以得出
ηnωEn=(η12η(n-1)n/η11η(n-1)(n-1))P
(4)
如令:τ12n=η12η(n-1)n/η11η(n-1)(n-1),则τ12n为单向路径12n的路径效率,所以能量接受子系统t和声源子系统s间的路径效率
(5)
式中:Pt为外界传入接受子系统t的功率;Ps为声源子系统s输出的功率,根据能量守恒,子系统t从邻接子系统接受的功率等于自身总损耗的功率,因而可以表示为Pt=ωηttEt,ηtt为总损耗因子。对于路径效率方法,主要传递路径一定满足路径效率值最大。

图1 n子系统构成的单向路径Fig.1 Single path of n subsystems
实际情况中,子系统之间的功率流动是极为复杂的双向流动,还会产生环状路径(Path with Loop)[18],因而如何获得所有路径的路径效率是一个十分棘手的问题。Craik认为可以通过对能量平衡方程中经典的SEA非对称矩阵(SEA Non-symmetric Matrix)变化,并展开成诺依曼级数(Neuman Series)的方式获得路径效率。
N子系统的能量平衡方程一般可以表示为
(6)
令式(6)中SEA非对称阵为H,子系统能量列向量为E,外界输入功率列向量为P,定义新矩阵S(i,j)=(ηji/ηii)(1-δij),D=diag(η11,,ηnn),I为n阶单位矩阵,则式(6)可以转化为
ω(I-S)DE=P
(7)
对式(7)再作变形,得到总体路径效率矩阵(I-S)-1,为了避免求逆运算,原矩阵可以展开成诺依曼级数的形式
(8)
根据定义,路径效率满足性质
τij=τik·τkj
(9)
由式(8)和式(9)可以说明级数∑Sk中每一项的物理意义,0阶项I中的对角元素表明各子系统对自身的路径效率恒为1,1阶项S中元素表示各子系统i和空间上邻接的子系统j直接耦合的路径效率,即ηji/ηii,高阶项Sk中元素则代表通过中间顶点间接耦合的路径效率。所以路径效率矩阵(I-S)-1并不能说明某一条路径的效率,其中元素(i,j)的物理意义为:顶点j~顶点i所有路径效率的和。
1.2 统计熵方法(SEM)
1960年Lyon等[19]在计算随机激励下的振动模态群的功率流时得出式(2),并得出子系统间的能量交换和模态能量差值成正比的结论。由式(2)也可以看出振动能量总是从模态能量高的子系统向模态能量低的子系统传递,这被认为是声振问题和热力学问题类比的基础[20],从而模态能量的物理意义类似于热力学中的温度。经典的统计能量法是以能量平衡方程作为基础,能量平衡方程也就是热力学第一定律在声振问题上的表述,而能量平衡方程只是解决了能量传递的数量问题并未解决能量传递的方向问题。Carcaterra和Le Bot对“声振-热力”对比加以完善,引入了熵分析方法,从而使得统计能量法可以直接从能量角度确定传递路径。
文献[15]中严格推导的声振温度表示为
T=E/kN
(10)
式中:k=1.38×10-23J/K为玻尔兹曼常数,声振温度正比于模态能量。根据克劳修斯熵的定义,子系统i的统计熵

(11)
如图2所示,任意两个子系统1,2构成的耦合系统,若声振温度T1>T2,则整个系统的熵

图2 两子系统SEA耦合模型Fig.2 SEA coupling model of two subsystems dS=dSrev+dSirr
(12)
(13)
(14)
式中: dSrev, dSirr分别为熵dS中的可逆过程和不可逆过程,由热力学中熵增原理可知,可逆过程dSrev=0,不可逆过程熵dSirr反应的是能量传递过程的自发程度,所以系统在耦合过程中产生的熵为dSirr。将式(10)、式(14)代入式(12),耦合过程的统计熵的产率为
(15)
式中:n1,n2分别为子系统1,2的模态数。对于统计熵方法,根据热力学第二定律,主要路径上统计熵产率的和也是最大的。
1.3 当前研究存在的问题
张文春采用路径效率方法分析振声源S到目标元t的噪声传递路径[21],高处利用统计熵的分析方法分析超大型邮轮的噪声传递路径[22]。由于方法推广的较少,目前存在以下几点问题:①研究只是针对噪声源及接受点位置固定的情况展开研究,还没有解决“多源-多接受点”的路径问题;②研究论述的方案到工程应用还有一段距离,并且在分析路径时大多做了传递路径形式的简化,例如只将噪声传递路径设定在声腔与声腔之间,或者对同一结构的不同模态子系统也做了压缩;③到目前为止没有针对两种方法的对比研究。
本文采用路径效率方法和统计熵方法分析声源和接受点处于任意位置的前N条主要的噪声传递路径。
2 研究方法及算法
上节论述的两种基于SEA的传递路径分析方法已经给出主要路径的判断条件,由于已经将结构之间的能量流动简化成模态群子系统之间的能量交换,因而可以通过图论的方式去研究声源到接受点之间能量传递的N条主要路径,物理问题也就抽象为数学问题。前N条最短路径问题是图论中的经典问题,成熟的算法主要有Dijkstra算法、Warshall-Floyd算法、MPS算法、遗传算法以及Yen算法[23-24],求解的关键就是将前N条主要路径问题转化为图论中的前N条最短路径问题。
2.1 主要传递路径的数学表述
(1) 赋权图及最短路问题
在简单图G=(V,E)中,V(G)={v1,v2,,vn}代表非空顶点集,E(G)={e1,e2,,en}代表不相交的边集,若对每一边vivj赋予一个实数,记为w(vivj),称为边vivj的权,图G的每一边都赋予权的图称为赋权图,将权写成矩阵形式,称为权值矩阵W,即
(16)
路(s,t)的边权之和称为该路的长,顶点s,t间路长最小的路称为最短路问题[25]。最短问题是经典的最优化问题,拥有大量的经典算法,可以转化为最短路问题的物理问题一般可以分为两类,用权值可以表示为
(17)
(18)
式中:p,q分别为路(i,k)和(k,j);wij,wik,wkj为权值矩阵中元素,显然,路径效率方法满足式(17),统计熵方法满足式(18)。
(2) 权值矩阵的构建
由于涉及工程应用,数量庞大的子系统间的邻接关系难以通过枚举方式找出[26],并且相较于路径效率分析方法,构建统计熵的权值矩阵需要的SEA参数更多。本文在VAone中进行统计能量建模分析,导出SEA非对称矩阵(SEA Non-symmetric Matrix)、模态能量矩阵以及模态数矩阵,SEA矩阵中耦合损耗因子不为零表示子系统之间邻接,这样仅仅通过计算就可获得权值矩阵。
对于统计熵方法,依据式(15)计算出子系统之间的统计熵的产率dSij/dt,统计熵权值矩阵为
(19)
对于路径效率方法,依据式(7)计算1阶路径效率矩阵S,由于要应用最短路算法,路径效率权值矩阵为
(20)
由式(19)和式(20)看出统计熵方法是单向有向赋权图,权值矩阵是非对称阵,传递路径是有限个;路径效率方法是双向有向赋权图,权值矩阵也是非对称阵,传递路径随着级数展开阶次增大而增多。
2.2 前N条的Warshall-Floyd算法
(1) 第一条最短路算法
Warshall-Floyd算法属于动态规划算法,可以用来计算多源最短路径,核心思想是判断从顶点i~j的最短路径是否通过顶点k,对权值矩阵中每一个元素都进行判断:ifW(i,j)>W(i,k)+W(k,j),W(i,j)=W(i,k)+W(k,j),最后得到任意两顶点间最短距离的矩阵U,算法时间复杂程度为O(n3),空间复杂程度为O(n2)[27]。得到最短距离矩阵U,从终点开始减去权值矩阵中元素,判断对应顶点是否位于最短路径中,依次获得最短路上的顶点。
(2)N-1条次最短路算法
经典算法需要通过改进才能计算后续的N-1条次最短路径,文献[24]给出了最简单的方式:通过删除最短路径中某条边得出新的子图,并对一系列子图重新计算最短路径,最后进行排序。本文首先运用Warshall-Floyd算法计算删除边后的次最短路径,然后用冒泡法对次最短路径进行排序。
3 研究对象与分析
本文取海洋工程船中间分段的2×3×4排布的24个舱室作为研究对象,激励为主机的结构噪声激励,加速度谱见表1。对24个SEA声腔和98块SEA板进行编号,编号1~24为声腔,编号25~318为板,一共有318个模态群子系统,将结构噪声加在“声腔-1”外侧“板-91”的横向弯曲(Transverse Flexure)方向,接受舱为“声腔-24”,研究噪声在这之间的前N条主要传递路径,VAone中的SEA计算模型如图3所示,且在中高频段(250~8 000 Hz)上子系统的模态数大于5,满足SEA分析要求。
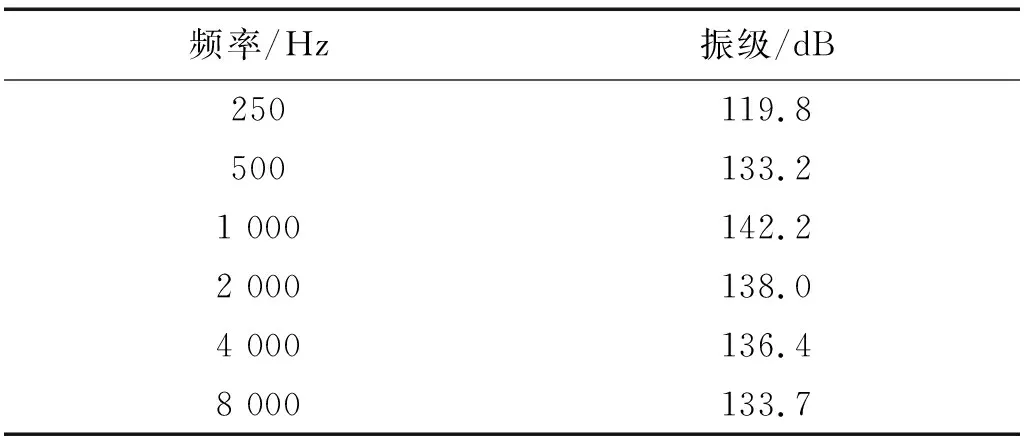
表1 结构激励频谱Tab.1 The spectra of structure-borne excitation

图3 SEA计算模型Fig.3 SEA simulation model
由于SEA板存在3个模态群子系统,分别为横向弯曲(Transverse Flexure)、面内拉伸(In-plane Extension)及面内剪切(In-plane Shear)。加载在“板-91”弯曲方向的结构激励会激起3个方向的模态群,并以这3个模态群作为初始噪声源向其他子系统传递能量。
3.1 传递路径的频率特性
计算的路径很多,选取两种方法下“板-91-F”到“声腔-24”的第一条主要传递路径为研究对象,计算结果见表2和表3。

表2 弯曲方向声源的路径效率法1 st主要传递路径Tab.2 The 1 st dominant transfer path of noise source in flexure direction by PEM

表3 弯曲方向声源的统计熵方法1 st主要传递路径Tab.3 The 1 st dominant transfer path of noise source in flexure direction by SEM
分析表2和表3可以得出:①两种方法计算得出的第一条主要路径完全不相同;②两种方法都说明,第一条主要传递路径随频率变化而改变,在中频段(250~1 000 Hz)以及高频段(4 000~8 000 Hz)的主要传递路径在各自方法中趋于一致。查看弯曲方向声源的其它次最短路径同样也呈现上述规律,说明这是主要传递路径在频域上的一般规律。
3.2 传递路径的模态群特性
模态群对传递路径的影响主要由两方面因素构成:①不同模态群的结构激励源;②传递路径上的不同模态群之间的耦合。因此,用统计熵方法分别研究拉伸、弯曲、剪切3个方向噪声源到“声腔-24”的第一条主要传递路径,同时用路径效率分析前3条弯曲方向噪声源的传递路径作为对比,计算结果见表2~表7。

表4 拉伸方向声源的统计熵法1 st主要路径Tab.4 The 1 st dominant transfer path of noise source in extension direction by SEM

表5 剪切方向声源的统计熵法1 st主要传递路径Tab.5 The 1 st dominant transfer path of noise source in extension direction by SEM
对比表3~表5中数据说明:①由统计熵产率,弯曲方向声源的第一条主要路径是其他两方向最大路径的3倍,弯曲方向传递作用更为显著;②250~2 000 Hz频段的前3条主要路径都包含子路径“73E-46S-46F-16-24”。对比表2、表6、表7可以说明:对于路径效率方法在中频段(250~2 000 Hz)弯曲模态群之间能量传递效果更好,高频段(4 000~8 000 Hz)拉伸模态群效率更高。
3.3 传递路径的能量分布
由3.1节分析可知,第一条主要传递路径在不同频率下不一致,所以研究算法每次求出的N(N≤8)条路径的能量权重。根据熵的定义,统计熵方法能够得出任意两条路径的传递能量的相对大小,但是统计熵的产率没有一个总量可以参考,无法得出该主要路径在所有路径中传递能量的权重,路径效率法可以得出任意两点间所有路径效率的和,但是无法比较不同频率时传递能量的多少。因此,要将两种方法结合起来研究传递路径的分布规律。

表6 弯曲方向声源的路径效率法2 nd传递路径Tab.6 The 2 nd dominant transfer path of noise source in flexure direction by PEM

表7 弯曲方向声源的路径效率法3 rd传递路径Tab.7 The 3 rd dominant transfer path of noise source in flexure direction by PEM
(1) 各频率下前3条主要传递路径的能量
利用统计熵方法计算出各频率下前3条主要传递路径,第2、第3条传递路径见表8和表9。

表8 弯曲方向声源的统计熵方法2 nd主要传递路径Tab.8 The 2 nd dominant transfer path of noise source in flexure direction by SEM

表9 弯曲方向声源的统计熵方法3 rd主要传递路径Tab.9 The 3 rd dominant transfer path of noise source in flexure direction by SEM
比较表3、表8、表9中数据说明:①各频率下前3条主要传递路径之间对比,频率越高能量传递越多,且高频段8 000 Hz的统计熵产率是中频段250 Hz的1×105倍,能量在高频段的前几条主要路径中更集中;②各频段前3条路径的统计熵差值不大,能量不是依托唯一路径传递的,可能是一小群路径传递大量的能量;③高频段声腔子系统之间的能量传递数量更多,因而高处的文章中传递路径的简化方式在高频段是可行的;④工程中可以仅通过计算高频段(4 000~8 000 Hz)的主要传递路径来确定整个频段下的主要传递路径,所以参照图4~图6前3条主要传递路径为:91F,1,2,4,6,8,16,24;91F,1,3,4,6,8,16,24;91F,1,3,5,6,8,16,24。
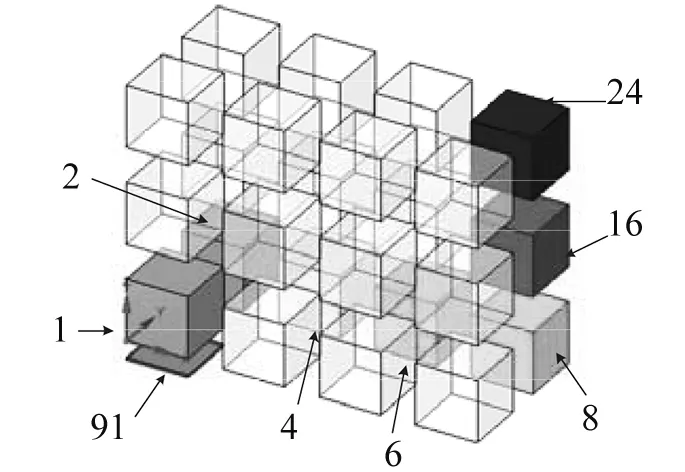
图4 全频段第1条主要路径Fig.4 The 1 st dominant transfer path in full-band
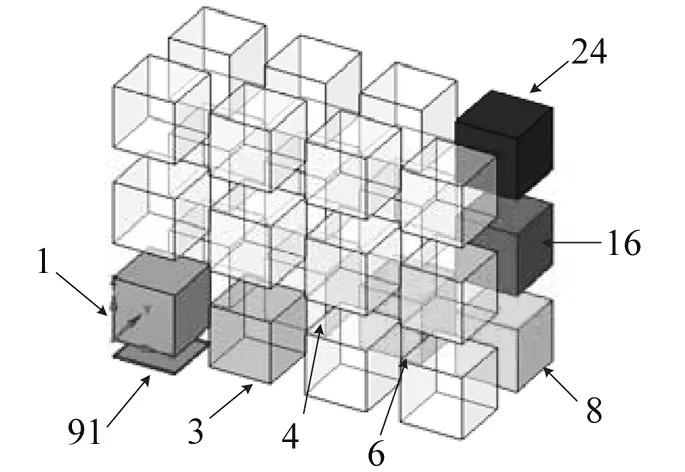
图5 全频段第2条主要路径Fig.5 The 2 nd dominant transfer path in full-band

图6 全频段第3条主要路径Fig.6 The 3 rd dominant transfer path in full-band
(2) 各频率下主要传递路径能量权重

通过“3.1~3.2”节的前3条主要路径计算结果,主要路径均为8个顶点,路径效率为7阶路径效率,所以对应的诺依曼级数展开阶数至少为8。邻接矩阵是唯一的,当展开阶数为8时,所有频率下路径数量已经为109 722 282。对于路径效率之和,因为级数是无数个项,由于1阶路径效率矩阵中元素S(i,j)<1,对于高阶路径效率矩阵中元素Sk(i,j)=∏S(m,n),因而也小于1,高阶路径效率矩阵趋于0矩阵,所以应该用尽可能大的阶数去近似路径效率的和。表10给出阶数为11时各频率下弯曲方向声源与“声腔-24”之间所有路径效率之和及前3条路径的权重。当级数阶数为11时,前3条路径的路径效率权重见图7。
表10和图7中数据可以说明:①前3条路径高频段的路径效率可以到72%,且高频段(4 000~8 000 Hz)前两条路径效率要高于第3条路径,所以在高频段前几条主要路径为能量的主要路径;②文献[21]的观点值得商榷,虽然中频段(250~2 000 Hz)传递能量比例低,并不是因为中频段路径数量比高频段多,而是中频段的能量在所有路径中比较分散,不像高频段集中于前几条主要路径中。

表10 11阶路径效率和及前3条路径权重Tab.10 The summation of 11-order path efficiency and the weights of the first 3 paths

图7 前3条路径在级数阶数为11时的权重Fig.7 The path efficiency weight of first 3 paths in 11-order path efficiency summation
3.4 噪声传递路径的验证
两种方法对噪声主要路径的评价依据不同,因而得出的路径也有差异,VAone软件是采用路径效率方法,能计算出与表2相同第1条路径,但无法给出其他主要路径以及具体模态群传递形式。结构噪声是通过结构子系统间的耦合振动传递能量,所以通过阻尼敷设来抑制主要路径上结构振动,来验证主要路径的正确性。
前文“3.1”节依据路径效率方法得出主要路径在中、高频段各不相同,并且路径效率理论缺乏统一评价标准,无法进行不同频段间的横向对比。为了尽可能消除不确定性,对于两种方法找出的各频段下前3条路径,在全频段(250~8 000 Hz)内计算敷设阻尼后的“声腔-24”的降噪效果,并对比两种方法降噪效果的算术均值来分析方法的可靠性,两种方法找出的路径统计结果见图8、图9,结构的两面统一采用20 mm的黏弹性高分子聚合物(Visco-elastic Polymer)进行敷设。前后的对比见表11和图10,可以看出:①相较于已集成在VAone软件中的路径效率法,统计熵方法找出的主要路径降噪效果更好,可相差1.3 dB(A);②由于只考虑阻尼隔声作用,对于3.3节得出的高频段以声腔为传递路径上节点的规律,多孔材料对于舱室内直达声的吸收,可以使得统计熵方法的传递路径有更好的降噪效果;③不能否定路径效率方法对传递路径的识别,路径效率方法有助于认识能量在中低频段的传递特点。

图8 路径效率法10条路径Fig.8 Ten paths calculated by PEM

图9 统计熵法6条路径Fig.9 Six paths calculated by SEM
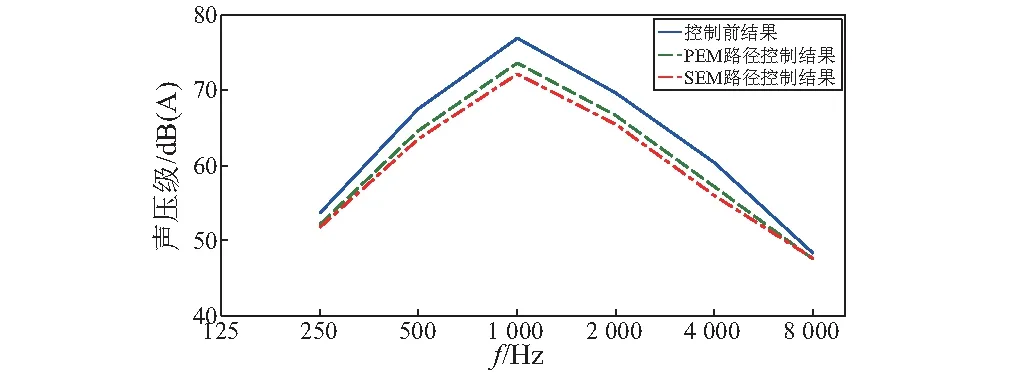
图10 降噪频谱对比Fig.10 The comparison of noise-reduction spectrum表11 降噪结果对比Tab.11 The comparison of noise-reduction
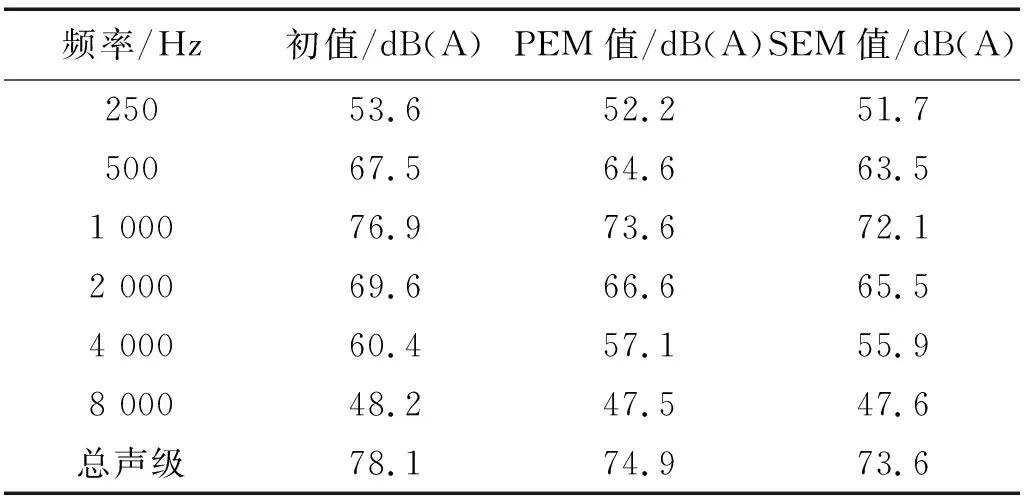
频率/Hz初值/dB(A)PEM值/dB(A)SEM值/dB(A)25053.652.251.750067.564.663.51 00076.973.672.12 00069.666.665.54 00060.457.155.98 00048.247.547.6总声级78.174.973.6
3.5 不同算法对传递路径分析的影响
前文总结了两种基于SEA理论的传递路径分析方法(PEM,SEM),并应用图论中算法求解前N条主要路径。第2节所述经典算法中,Dijkstra算法是单源最短路径算法[28],MPS、Yen等算法也都是基于Dijkstra算法的内核,Warshall-Floyd算法是多源最短路径算法。因为本文“3.2”节研究多源(弯曲、拉伸、剪切)情况下的传递路径特点,Warshall-Floyd算法在计算最短距离的权值矩阵后,可以一次性给出所有节点对的最短路径,而Dijkstra算法则要多次计算不同源下的最短距离权值矩阵,所以本文选用最简洁的Warshall-Floyd算法。
为了进一步比较算法对传递路径的影响,参照文献[22]思路,在SEM框架下分别用Dijkstra算法和Warshall-Floyd算法对比验证最主要的弯曲方向声源的前3条最短路径,如表12(篇幅所限仅列出250 Hz的结果,其他频率下结论均相同)可以看出在删除边理论下两种算法的前3条最主要传递路径是一致的。同理,对PEM理论也采用Dijkstra算法与Warshall-Floyd算法分析弯曲声源,同样得到的结果也一致,所以不同的图论算法不会影响主要路径分析的唯一性。

表12 250 Hz下算法结果对比Tab.12 The comparison of results by two algorithms in 250 Hz with SEM
图论中Dijkstra算法只能求非负权值的最短路径,是为了避免负环路引起的死循环,按照本文权值矩阵定义式(19)、式(20)Dijkstra算法可以推广为适用于权值同号的矩阵。根据路径效率定义S(i,j)=[ηji/(ηi+∑ηik)](1-δij),对于实船上大尺寸的不规则舱室,板、腔之间模态密度差异悬殊,依据“能量互易原理”有ηji≫ηij成立,可能会出现少数大于1的元素S(i,j),进而出现权值异号的情况。Dijkstra算法的优势在于计算速度快于Warshall-Floyd算法,虽说从上一段的分析结果来看,Dijkstra的计算并未出现该情况,但本文研究侧重于对比两种不同理论下传递路径的差异,且模型阶数较小,所以牺牲了运算速度采用更为保守的多源动态规划算法Warshall-Floyd进行分析。本文模型阶数在300左右,Dijkstra算法还没有显现出较大的计算优势,当实际工程模型中权值矩阵阶数成千上万时,采用Dijkstra算法进行传递路径分析会显著的缩短运算时间。
4 结 论
本文在统计能量分析理论框架内,通过路径效率方法与统计熵方法分析了船舶结构噪声的传递路径,旨在从前N条主要传递路径上来阻断船舶结构噪声的传播,从而降低目标舱室的声压级响应。文章综合比较了两种理论框架下主要传递路径的特点,得出如下几点结论:
(1) 船舶结构噪声的传递路径与分析频段相关,在中频段(250~1 000 Hz)以及高频段(4 000~8 000 Hz)传递路径几乎一致,路径效率方法和统计熵方法得出的主要路径不一致,对统计熵方法得出的主要路径实施降噪控制措施能获得更好的效果。
(2) 船舶动力设备激发的结构噪声,噪声源弯曲方向的模态群输出了主要的能量。同时,路径效率方法得出,在低频段主要依靠结构子系统间的弯曲模态群传递能量,高频段主要是拉伸模态群传递能量;统计熵方法得出,高频段能量传递的主要形式是声腔与声腔,并不通过板材耦合,所以对于噪声响应大的临近舱室,隔声处理尤为重要。
(3) 由于高频段传递路径的一致性,且高频段统计熵产率最高,因而工程上可以把统计熵方法求解的高频段主要传递路径作为全频段的主要传递路径。
(4) 路径效率法说明传递路径是结构的固有属性,在中低频段能量比较分散,因而前几条路径传递的能量不是十分显著,而高频段能量主要集中在前几条路径中,说明传递路径分析能为船舶高频段降噪提供指导。
