层叠P阶多项式主成分分析在轴承故障诊断中的应用

牟 亮, 王 凯, 李 彦，於 辉

(四川大学 制造科学与工程学院，成都 610065)

滚动轴承是旋转机械设备中一种重要的零部件，它的主要功能是支撑机械旋转体，降低其运动过程中的摩擦因数，并保证回转精度。其运行状态直接影响到整台机器的使用寿命、可靠性。由于滚动轴承的故障多出现在滚动体、内外圈壁等隐蔽位置，体现为轻微点蚀、轻微裂纹等故障形式，工程人员检查时不易观察和判断。所以对滚动轴承的潜在故障诊断具有十分重要的意义[1]。

传统的轴承故障诊断常采用解调分析。其中，经典的解调法是带通检波解调法[2]。在其基础上又演变出了基于谐波小波变换解调方法[3]。上述方法都有着不错的检测效果，但是需要工程人员熟练掌握各种解调技术；且找出调制信号丰富的、具有区分能力的特征高度依赖工程技术人员的经验。因此，如何自动地对信号快速、准确地完成分析，辨别出轴承的故障类型成为了一个亟待解决的问题[4]。

对此，国内外学者围绕轴承故障的智能诊断开展了广泛的研究。Lei等[4]利用一种深度学习的方法，通过一个具有三层神经网络的稀疏过滤器训练原始数据,将高维的故障轴承数据转换为低维的编码矢量。为了增加提取的编码矢量的鲁棒性，其在训练样本中加入了一定统计特征的噪声，使得训练后的网络对有轻微扰动的信号也具有较高的识别精度。Amar等[5]提出了一种针对在低信噪比条件下新型振动光谱成像的特征增强方法，通过阈值化2D平均过滤器增强信号特征，采用人工神经网络完成特征分类。Zhang等[6]提出一种基于多尺度熵和自适应模糊神经推理系统相结合的方法，通过计算相互耦合的机械零部件间的动态非线性来提取轴承的特征，将提取的特征输入模糊神经网络，推理出轴承故障类型。Zheng等[7]提出利用局部尺度特征分解法将轴承振动信号分解为多个固有尺度元素，再利用模糊熵计算出主要的固有尺度元素，最后将得到的元素输入模糊神经推理系统，完成轴承的故障诊断。Zhang等提出了一种集合了置换熵、整体经验分解和最优支持向量机的机器学习分类方法。李锋等提出了一种判别式正交线性局部切空间排列方法，将时域故障信号和频域故障信号相耦合，提高了故障辨识能力。

上述方法大都采用了浅层或深度人工神经网络。多层次的网络结构能够高度约简特征，使提取的特征获得较好的鉴别能力和鲁棒性。然而，上述基于深层神经网络的故障诊断方法也存在一些不足。首先，要获得一个好的深度神经网络学习模型，需要寻优学习许多参数(层与层之间的权重参数，网络隐藏层的层数，每一层神经元的个数、权重衰减速率、学习速率等)，这将导致计算资源和内存开销的增加，通常需要配置高性能GPU来提高模型学习的效率。其次，为了训练深度神经网络模型还需要提供海量的带标签的训练数据，当训练数据较少时深度神经网络模型容易欠拟合导致其泛化学习能力降低，为了防止模型欠拟合还要引入调优算法，这使得深度神经网络的模型变得复杂，计算过程变得繁琐。基于以上分析，提出一种层叠P阶多项式主成分分析方法。该方法利用深度神经网络多层次特征约简的思想，结合主成分分析高效的特征约简能力，学习具有优秀鉴别性能的特征。试验结果表明，提出的方法能获得很高的故障识别精度，是一种有效的故障诊断方法。

1 主成分分析方法概述

主成分分析(Principal Components Analysis，PCA)是一种简化数据集的技术[8]。它的目的是在尽可能多的保留原始变量表达的前提下，将一组包含有大量相关变量的高维数据集转换为更低维度的变量不相关的特征集。通过主成分分析，可以求得一个由各个特征向量为基的子空间，通过其与原始数据矩阵正交，使原始数据投影至该子空间。在机器学习领域，主成分分析得到的特征包含数据中的关键信息，因此常用于数据的特征提取[9]。此外，主成分分析也可用于信号的降噪处理[10]。

PCA的一大优点是可通过无参数化计算获得去相关的特征。PCA尽管计算简单、高效，但仍有如下缺点，仅仅通过PCA获取的特征的可鉴别性能仍然有限；PCA算法可有效表征线性数据而无法直接表征非线性数据的维度特征；PCA算法的泛化能力不强，无法准确表示非高斯分布数据的维度特征。

2 层叠P阶多项式主成分分析方法

2.1 P阶多项式主成分分析

为了进一步增强通过PCA映射后特征的可鉴别能力及对非线性数据的有效表征，提出一种P阶多项式主成分分析(P-order Polynomial Principal Component Analysis, PPCA)法。该方法将P阶多项式作为非线性映射函数，将原始数据集映射至高维线性空间，然后对高维线性空间中的数据集进行主成分分析。该方法的优点在于剔除了原始数据中的部分冗余特征，将原本线性不可分的数据集变换为线性可分的数据集，增强了映射后特征的可鉴别能力及PCA算法的泛化能力。

设原始数据集X=[x1,x2, ,xn]∈Rd×n，其包含n个d维的变量。各个变量都经过了中心化处理，即各个变量均值为0。首先，将数据集X代入P阶多项式函数中

k(XT,X)=〈φ(XT)·φ(X)〉= [(XT·X)+1]p(p=2)

(1)

式中:φ为一种非线性映射函数，通过φ可将原始数据X映射到高维的空间F, 即φ:X→F。

根据Mercer定理[16]：假设存在两个映射函数φ1:X→F1,φ2:X→F2，对任意的ω1∈F1，如果存在ω2∈F2使得〈ω1,φ1(X)〉=〈ω2,φ2(X)〉，则可获得在高维空间F中线性可分的数据，且无需知道非线性映射函数φ的具体形式,即内积〈φ(XT)·φ(X)〉的值与φ的表达形式无关，其值可由P阶多项式直接计算得到。利用Mercer定理，如果要使式(1)中的原始数据X在高维空间F中线性可分，只需将式(1)中P阶多项式的参数p设置为大于1的整数即可，即p=2,3,4,5,，分别对应不同的P阶多项式。参数p的取值不同，原始数据集X映射到高维空间F的结果就不同，本文提出的方法中参数p的取值，根据试验的结果来确定(详见3.1节)。

通过式(1)求出数据集X在更高维度空间(希尔伯特空间)中的内积〈φ(XT)·φ(X)〉。对高维空间中的数据集φ(X)=[φ(x1),φ(x2), ,φ(xn)]∈Rd×n进行主成分分析，求出特征子空间。通过与数据集φ(X)正交，使数据集φ(X)投影至该子空间。在该子空间中，数据间的方差最大的基被称为第一主成分，数据间的方差第二大的基为第二主成分，各主成分按降序排列，构成特征子空间。假设特征子空间V=[v1,v2, ,vk]∈Rd×k由k个的特征向量构成。以第一主成分v1为例，数据集φ(X)投影至v1上获得的方差最大，可转换为如下优化问题

(2)

(3)

(4)

求出式(4)关于v1的极大值，即是求出v1对的偏导数为0的点。求得式(4)关于v1的偏导数为

(5)

把希尔伯特空间内积矩阵E{φ(X)φ(X)T}记作M，式(5)可进一步简写为

(6)

至此，得到一个广义的求取特征值和特征向量的问题。通过求出的各个特征向量构成特征子空间，将数据集与特征子空间做正交运算，完成数据集向特征子空间的投影。

2.2 层叠P阶多项式主成分分析网络

提出的PPCA方法虽然克服了PCA不能直接处理非线性数据的缺点，然而，通过单一层次PPCA抽象出的特征可鉴别能力仍然有限，分类识别复杂的轴承故障信号精度较低。基于此，构建了层叠PPCA(Stacked PPCA, SPPCA)网络结构，其融合了深度神经网络具有学习多层次、高度约简特征的优势，优化了原单层特征约简时，特征鉴别能力不足的问题。

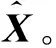
图1 SPPCA 轴承故障诊断网络Fig.1 SPPCA bearing fault diagnosis network

求取总体映射误差最小值，需在原始空间中重构出映射后的目标子空间特征，即是将约简后的子空间特征还原到与原始数据集相同的维度。设原始数据集X=[x1,x2, ,xn]∈Rd×n含n个数据点，各数据点具有d个特征维度；其依次与特征子空间V=[v1,v2, ,vk]∈Rd×k(k个的特征向量)、特征子空间U=[u1,u2, ,ub]∈Rk×b(b个的特征向量)、特征子空间W=[w1,w2, ,wc]∈Rb×c(c个的特征向量)做正交运算，提取出子空间特征H=[h1,h2, ,hn]∈Rc×n。

H=WTUTVTX,H∈Rc×n

(7)

(8)

式中:xi∈Rd×1;hi∈Rd×1。总体映射误差为各个数据点欧式距离的总和

(9)

为了求取总体映射误差极小值，利用一种处理非线性函数全局极小值的方法——梯度下降算法，分别求出总体映射误差ε关于特征子空间W,U,V的偏导

(10)

以特征子空间W为例，对其进行更新迭代

(11)

对特征子空间U和V的更新依然采用式(11)的方式，本文不再赘述。式(11)中α被称为学习速率，一般情况下取大于0的实数。通过式(11)总体映射误差会沿一定梯度方向下降，最后无限逼近其极小值。

完成特征子空间的更新之后，将原始数据集依次与更新后的特征子空间V,U,W进行正交运算获得目标子空间特征H。此时，目标子空间特征H与原始数据集X的总体映射误差最小。目标子空间特征具有高保真性。

SPPCA方法流程如下：

步骤1 将原始数据集x代入P阶多项式函数，求出其在高维希尔伯特空间中内积φ(XT)·φ(X);

步骤2 根据式(2)～式(5)求出希尔伯特空间内积矩阵E{φ(X)φ(X)T}对应的特征向量vi，各个特征向量组合，构成特征子空间V={v1,v2, ,vk};

步骤3 将原始数据集X与特征子空间V做正交运算，求出子空间特征Y;

步骤4 以子空间特征Y为输入，重复步骤1～步骤3，输出子空间特征Z;

步骤5 以子空间特征Z为输入，重复步骤1～步骤3，输出目标子空间特征H;

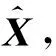
步骤7 将原始数据集X投影至更新后的特征子空间上，通过层叠学习，求出目标子空间特征H;

步骤8 将目标子空间特征H按照表2中的比例分割为训练集与测试集，通过KNN(K-Nearest Neighbor)分类器判定测试集所属类别，完成故障诊断。

3 试验分析及验证

3.1 试验数据库及试验方法

提出的SPPCA方法对高维度、非线性、多作用域的复杂旋转机械故障信号，进行了层叠学习提取出高分辨性的特征。克服了传统信号处理中手动特征提取对先验知识及专家经验的依赖，减轻了依靠人工识别的劳动强度。试验采用凯斯西储大学轴承数据中心电气工程实验室的滚动轴承故障模拟试验平台[13]采集的轴承数据。该试验平台如图2所示。其设备从左到右依次为电动机(2 hp)、加速度传感器、转矩传感器、功率计。试验数据通过安装在电动机驱动端正上方的加速度传感器收集。

图2 斯西储滚动轴承故障模拟试验平台Fig.2 Fault simulation experiment platform of bearings

试验中的轴承的故障磨损形式为人工电火花加工的单点点蚀磨损。单点点蚀故障分布在轴承内圈(IF)、滚动体(RF)、外圈(OF)。其中外圈的单点点蚀位置与轴承承载区的位置不同，外圈有3种损伤位置，分别是3点钟、6点钟和12点钟方向。试验中只选用了6点钟方向的单点点蚀作为外圈的点蚀损伤形式。在各个位置分布的单点点蚀都存在3种点蚀直径，分别是0.177 8 mm, 0.355 6 mm, 0.533 4 mm。每一个位置分布上的每一种单点点蚀直径都被视为一种故障类型(试验中将其称为工况)，所以试验中共有9种工况，加上一类没有故障的工况(Normal，N)，一共有10种工况。每一种工况对应的简称见表1。对每一类工况进行故障信号采样时，会在4种电动机转速下(1 797 r/min，1 772 r/min，1 750 r/min，1 730 r/min)进行重复试验。试验把4种转速下采集的同一工况的所有故障信号视为同一类。

表1 不同点蚀所对应的轴承故障代号Tab.1 The bearing fault code to different type of pitting correspondence

试验中加速度传感器的采样频率为12 kHz，每10 s采集120 000个样本点，将每一类的120 000个样本点划分为100个子样本，每个子样本有1 200个样本点。由于每一类工况在采样时，会在4种电动机转速下进行重复试验，这样试验中每一种工况的子样本总数变成了400(4×100)。试验中通过加速度传感器采集嵌套在电动机主轴上的滚动轴承的加速度信号，图3表示的是在电动机转速为1 730 r/min时，采集的十类工况的加速度波形图。每幅子图的横坐标显示的是采样时间段，纵坐标是不同时刻下电动机驱动端轴承加速度值。

图3 十类工况的加速度波形图Fig.3 The time-domain vibration waveform diagram of ten operating mode

试验对4种电动机转速下的数据样本的分割采用了相同的6种的训练/测试集分割比例，分别是10∶90，15∶85，20∶80，25∶75，30∶70，40∶60，见表2。比如训练/测试集的分割比例为10∶90，则选取样本总数前10%的样本作为训练样本，剩下的90%作为测试样本。

通过SPPCA提取到的目标子空间特征H中，每个特征可被表达为特征直方图。试验采用欧式距离来计算任意两个特征h和h′之间的相似度，见式 (12)。

(12)

表2 训练/测试集的数据分割比例Tab.2 Data segmentation ratio of reference/test set

式中：n为特征直方图h(h′)的维度。

试验采用K最近邻算法进行分类。通过式 (12)，K最近邻算法计算每个测试样本与训练样本间的相似度，取前K个具有最大相似度的训练样本的类别投票作为该测试样本的预测类别。参照文献[14]，试验中采用交叉验证的方法来确定K的取值，当K=3时，获得了最高的识别精度。

提出的SPPCA方法将原始数据集X从1 200维抽象成为600维子空间特征Y，然后将子空间特征Y抽象成300维子空间特征Z，最后，抽象为100维的目标子空间特征H。其目标子空间维度的估计方法为

(13)

式中：λj为希尔伯特空间内积矩阵E{φ(X)φ(X)T}的非零特征值;d为原始数据集X的特征维度1 200。计算出满足约束条件的c的取值范围，从中选取一个合适的值作为目标子空间特征H的维度。

本文还试验了其他特征学习策略，比如，从1 200维抽象至800维，从800维～400维等。通过试验对比，确定了本文的特征学习策略。其能获得更加本质的原始数据集的拓扑结构，提取的特征具有更强的鉴别能力；故障诊断精度能够达到最高。

提出的SPPCA方法中，式(1)中P阶多项式参数p的具体取值，本文采用轴承故障诊断的分类精度来确定。试验中p的取值依次取2, 3, 4, 5时，在不同的训练样本占比下(10%，20%，30%和40%)，分别计算了SPPCA方法的轴承故障分类精度。如图4所示，当p的取值增加时，在不同训练样本占比下，SPPCA的分类精度都在降低，当p的取值为2时，SPPCA的分类精度最高。因此，式(1)中P阶多项式参数p取值确定为2，即p=2。

3.2 试验结果比较及分析

试验验证了PCA方法与提出的PPCA及SPPCA方法在故障诊断性能上的差异，试验对同一数据集分别采用上述3种方法重复进行了5次对比试验，将每次分类精度结果收集后求平均值。图5与图6是3种诊断方式在不同数据分割比例下对应的分类精度结果。

如图5所示，经过P阶多项式函数的非线性映射后提取出的特征具有更好的区分性能。且SPPCA相比于单层PPCA，诊断精度平均提高了6%。这也印证了前文的说法：经过层叠学习过程，能够得到更加抽象的数据特征，从而提升对故障类别的鉴别能力，提高分类精度。并且相比前文提到的神经网络算法，经过SPPCA处理后的数据对训练集大小并不敏感，训练集在占比较小时，分类精度依然很高。为了试验方法的可靠性，对采样频率为48 kHz时采集到的轴承故障数据做了重复试验，结果如图6所示。

图4 在p的不同取值下SPPCA对应 的轴承故障分类精度Fig.4 The average classification accuracy of bearing faults corresponding to different values of p

图5 3种诊断方式结果比较 (采样频率12 kHz)Fig.5 The comparison of three diagnosis methods (sampling frequency 12 kHz)

图6 3种诊断方式结果比较 (采样频率48 kHz)Fig.6 The comparison among three diagnosis methods (sampling frequency 48 kHz)

如图7所示，原始数据集X经过(a)PCA方法、(b)PPCA方法和(c)SPPCA方法特征约简后得到了子空间特征H的主成分。通过抽取子空间特征H中前三维的主成分，绘制了散点图予以显示。其中横轴表示第一主成分(PC1)，纵轴表示第二主成分(PC2)，竖轴表示第三主成分(PC3)。三个主成分分别对应试验中加速传感器采集的加速度信号的主成分，其物理单位为m/s2。从图7可知，相比于PCA方法，提出的PPCA和SPPCA网络约简后获得的子空间特征H，使得异类数据间的区分更加明显，同类数据聚合的更加紧密；提取的特征具有更好的可区分性。SPPCA获取的数据聚合效果比PPCA更好，例如图7(c)中 RF-3和N的聚合效果优于图7(b)。

需要说明的是：数据集中每种工况下均有400个样本点，图7中只画出了100个样本点。其提取方式为从每个工况中4种电动机转速下分别提取前25%数据。

表3对比了提出的方法与其他研究者提出方法的在最终分类的精度上的差异。文献[6-7]、文献[15]中将全体轴承故障信号数据的10%作为训练样本，剩余的90%作为测试样本。文献[20]则采用30%的轴承故障信号数据作为训练样本，而剩余70%的数据用于测试。文献[17-19]使用40%的轴承故障信号数据作为训练样本，而剩余60%用于测试。文献[6]提出的方法获得了97.5%分类精度。文献[7]提出的局部尺度特征分解法在7种样本工况条件下，获得了96.43%的分类精度。文献[15]利用稀疏自编码神经网络学习信号特征，获得了96.76%的分类精度。文献[17]提出的自适应地图(A Self-Organizing Map ,SOM)方法，达到了95.7%的分类精度。文献[18]提出了置换熵、整体经验分解和最优支持向量机结合的机器学习分类方法，达到了97.67%的识别精度。文献[19]提出了一种判别式正交线性局部切空间排列方法，获得了98.64%分类精度。文献[20]提出一种有监督不相关局部Fisher判别分析方法，获得了81.25%的识别精度。提出的SPPCA方法对训练样本占比分别为10%，20%，30%和40%的4种情况都进行了故障诊断试验，如表3所示。提出的SPPCA方法在4种训练样本百分比情况下均获得了99%以上的识别精度，并随着训练样本百分比的增加识别精度有小幅度提升。验证了提出的SPPCA方法基于层叠学习获得的特征具有很好的可区分性，提出的方法是一种有效的智能故障诊断方法。

图7 目标子空间特征H散点图Fig.7 The scatter plots of subspace features

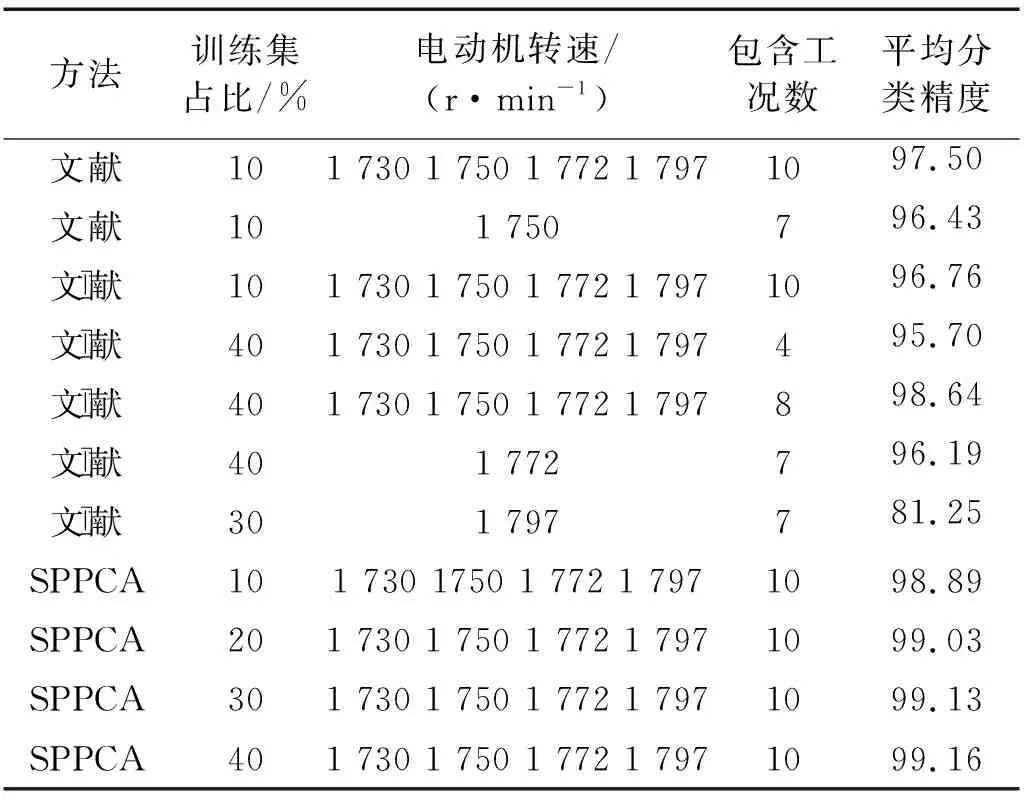
表3 SPPCA方法与其他方法关于轴承故障分类精度的比较Tab.3 The comparison between SPPCA and other methods about the classification of bearings fault diagnosis

4 结 论

本文构造的SPPCA网络模型能够深度挖掘故障轴承的特征信息。SPPCA继承了PCA方法高效约简特征维度的优势，并将PCA方法与P阶多项式映射结合，提出PPCA方法，获得了对非线性数据处理的能力。通过层叠地运用PPCA方法构建了SPPCA网络，其层叠学习方式，强化了特征约简过程，最大化异类故障数据边界,最小化同类故障数据边界，实现了高精度的类判别。并在网络中引入最小化映射误差，确保经过SPPCA映射后的故障轴承数据样本不失真。试验结果证明，本文提出的SPPCA方法针对含有噪声干扰多的复杂轴承信号具有深度抽象特征的能力，能够准确识别轴承故障类型。